
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Немесе комбинаторика 5 страница
|
|
|
|

7. 45-ке бөлінетін цифрлары арифметикалық прогрессияның тізбектес мүшелері болатын барлық үш таңбалы сандарды тап.
8. 250000-нан кем тізбектелген 25 құрама сан табылатынын дәлелде.
Нұсқау: Тізбектес 25 натурал санды  деп белгілеп алайық. Егер
деп белгілеп алайық. Егер 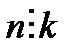 болса
болса 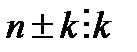 деген заңдылықты ескере отырып,
деген заңдылықты ескере отырып,
егер 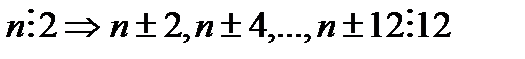
 болады да
болады да  түрінде болмақ.
түрінде болмақ. 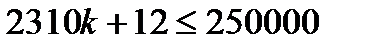 шарттарын қанағаттандыратындай етіп k-ны таңдаймыз. Енді
шарттарын қанағаттандыратындай етіп k-ны таңдаймыз. Енді 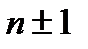 құрама сан болатындай етіп k - ны таңдау керек.
құрама сан болатындай етіп k - ны таңдау керек.
Мәселен n-1 саны 13-ке, n+1 cаны 17-ге бөлінетіндей етіп k -ны таңдасақ жеткілікті.
n = 13s + 1 = 17m-1 =>  ,
,  => k=?
=> k=?
9. Берілген натурал санға әр секунд сайын 554 немесе 777 саны қосылатын болса:
а) Белгілі уақытта соңғы үш цифры бірдей сан шығатынын дәлелде.
б) 2007 санына есептің шартын қолдасақ соңғы үш цифры бірдей сан шығу үшін ең қолайлы және ең қолайсыз жағдайларда қанша секунт уақыт керек.
Нұсқау:  болатындықтан санның соңғы үш цифрының өзгеруіне 777 саны екі рет қосылуы 554 саны бір рет қосылуымен бірдей әсер етеді. Немесе қосындыдағы 554-ті екі 777-мен алмастыру арқылы уақытты ұзартуға болады. Сондықтан 554 саны қосылса қолайлы жағдайға есептеледі.
болатындықтан санның соңғы үш цифрының өзгеруіне 777 саны екі рет қосылуы 554 саны бір рет қосылуымен бірдей әсер етеді. Немесе қосындыдағы 554-ті екі 777-мен алмастыру арқылы уақытты ұзартуға болады. Сондықтан 554 саны қосылса қолайлы жағдайға есептеледі.
а)  болатындықтан кез келген бүтін c саны үшін
болатындықтан кез келген бүтін c саны үшін  теңдеуінің шексіз көп шешімі болатынын, c -ні соңғы үш цифры бірдей қалауынша алынған (берілген саннан үлкен) санмeн берілген санның айырмасы ретінде алсақ есеп дәлелденеді.
теңдеуінің шексіз көп шешімі болатынын, c -ні соңғы үш цифры бірдей қалауынша алынған (берілген саннан үлкен) санмeн берілген санның айырмасы ретінде алсақ есеп дәлелденеді.
1.4.2. Диофант теңдеулерді шешудің
дербес тәсілдері
1. Көбейткіштерге жіктеу тәсілі
1- Есеп:  теңдеуінің бүтін шешім-дерін тап.
теңдеуінің бүтін шешім-дерін тап.
Шешімі: 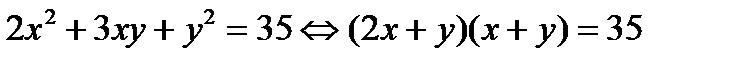
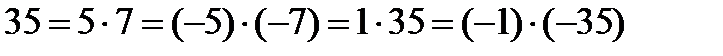 және х; у- бүтін сандар болатындықтан байланысты жүйелерді шешу арқылы (2;3), (-2;9), (-2;-3), (2;-9), (34;-33), (-34;69), (-34;33), (34;69) пар сандары теңдеудің шешімі болатынын анықтаймыз.
және х; у- бүтін сандар болатындықтан байланысты жүйелерді шешу арқылы (2;3), (-2;9), (-2;-3), (2;-9), (34;-33), (-34;69), (-34;33), (34;69) пар сандары теңдеудің шешімі болатынын анықтаймыз.
2-Есеп:  теңдеуінің бүтін шешімдерін тап.
теңдеуінің бүтін шешімдерін тап.
Шешімі: 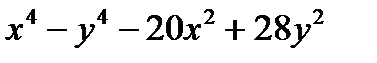 =
=
=  =
=
= 
= 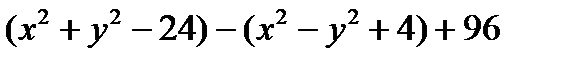 болатындықтан берілген теңдеу
болатындықтан берілген теңдеу  түрінде жазылуымен қатар
түрінде жазылуымен қатар 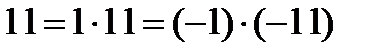 болатынын ескеріп алдыңғы есептегідей барлық мүмкін жағдайды қарастыру арқылы (2;-3), (-2;-3), (4;3), (-4; -3),(-2; 3), (2;-3), (-4;3), (4; -3), шешімдерін табамыз.
болатынын ескеріп алдыңғы есептегідей барлық мүмкін жағдайды қарастыру арқылы (2;-3), (-2;-3), (4;3), (-4; -3),(-2; 3), (2;-3), (-4;3), (4; -3), шешімдерін табамыз.
3-Есеп:  теңдеуінің бүтін шешімдерін тап.
теңдеуінің бүтін шешімдерін тап.
Шешімі: Берілген теңдеуді  деп түрлендірейік. Бұдан
деп түрлендірейік. Бұдан 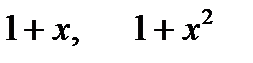 сандары
сандары 
-нің бөлгіштері болады. Немесе

 бұдан
бұдан 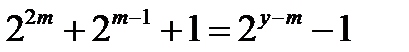 немесе
немесе  болады. Төмендегі жағдайларды қарастырайық.
болады. Төмендегі жағдайларды қарастырайық.
1. m=0 болсын.  немесе
немесе  және
және 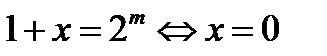
2. m>0 болсын.  және
және -лар бүтін
-бүтін және
 ,
, 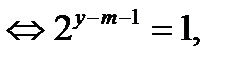
 немесе
немесе 
 олай болса теңдеудің (0;0), (1;2) деген екі бүтін шешімі бар.
олай болса теңдеудің (0;0), (1;2) деген екі бүтін шешімі бар.
4-Есеп: теңдеуінің натурал шешімдерін тап.
Шешімі: а)  (тақ)
(тақ)
б) 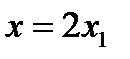 (жұп) eкі жағдайды қарастырайық:
(жұп) eкі жағдайды қарастырайық:
а) санын үшке бөлгенде қалдық 2 ге тең. Ал  -ді 3 ке бөлгенде 1- қалдық қалатындықтан теңдеудің бүтін шешімі жоқ.
-ді 3 ке бөлгенде 1- қалдық қалатындықтан теңдеудің бүтін шешімі жоқ.
б) 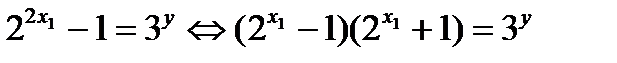 немесе
немесе - саны тізбектелген екі тақ санның көбейтіндісіне жіктелу керек. Бұл
 болғанда ғана мүмкін болады. Сондықтан
болғанда ғана мүмкін болады. Сондықтан  немесе x1 = 1. Олай болса теңдеудің (2;1) деген бір ғана бүтін шешімі болады.
немесе x1 = 1. Олай болса теңдеудің (2;1) деген бір ғана бүтін шешімі болады.
5-Есеп: xy = x + y теңдеуінің бүтін шешімін тап.
Шешімі: Теңдеуді 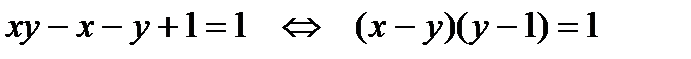 түріне келтірейік.
түріне келтірейік.  және х, у – бүтін сандар болатынын пайдаланып мүмкін екі жағдайды қарастыру арқылы (0; 0), (2; 2) шешімдерін табамыз.
және х, у – бүтін сандар болатынын пайдаланып мүмкін екі жағдайды қарастыру арқылы (0; 0), (2; 2) шешімдерін табамыз.
6-Есеп:  теңдеуінің жай сан шешімін тап.
теңдеуінің жай сан шешімін тап.
Шешімі: 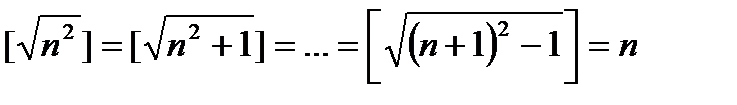 болатындықтан
болатындықтан
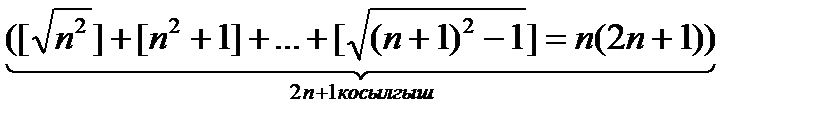
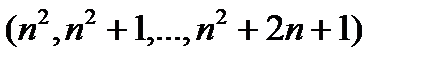 - тізбегінің мүшелер саны 2n+1. Олай болса
- тізбегінің мүшелер саны 2n+1. Олай болса 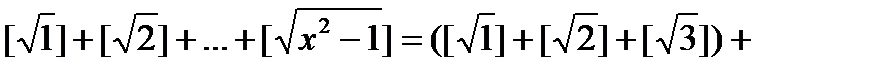
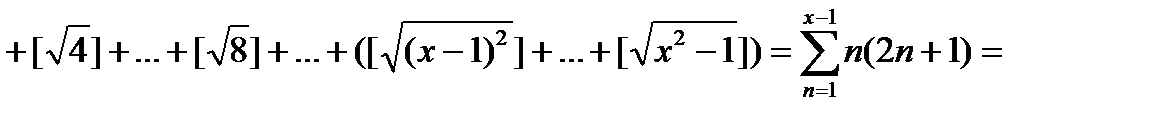
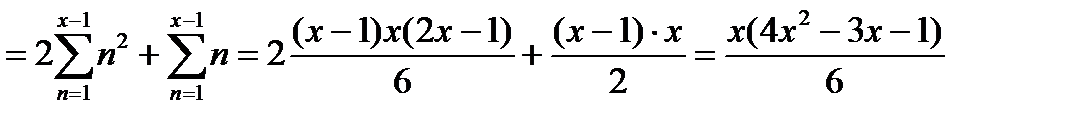
болады да берілген теңдеу  теңдеуіне ауысады.
теңдеуіне ауысады. 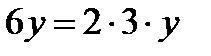 түріне жіктелетіндіктен есеп шарты бойынша
түріне жіктелетіндіктен есеп шарты бойынша
a) x=2, б) x=3, в) x=y және x, y жай сан болатын жағдайларды қарастыруға тура келеді.
a) 
б) 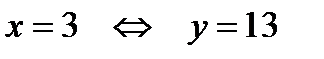
в)  теңдеуінің шешімі жай сан болмайды. Олай болса есептің шешімі (2;3), (3;13) пар сандар ғана.
теңдеуінің шешімі жай сан болмайды. Олай болса есептің шешімі (2;3), (3;13) пар сандар ғана.
7-Есеп: 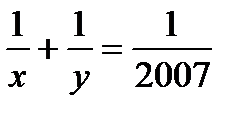 теңдеуінің натурал сандар жиынында неше шешімі болады.
теңдеуінің натурал сандар жиынында неше шешімі болады.
Шешімі: Теңдеуге элемантар түрлендіру жасап  немесе
немесе  түріне келтірейік.
түріне келтірейік. санын неше тәсілмен екі натурал санның көбейтіндісіне жіктеуге болса сонша натурал шешім шығады. Және
 санын екі натурал санның көбейтіндісіне 9 тәсілмен жазу мүмкіндігі бар екеніне көз жеткізу оңай. Олай болса берілген теңдеудің 9 натурал шешімі бар.
санын екі натурал санның көбейтіндісіне 9 тәсілмен жазу мүмкіндігі бар екеніне көз жеткізу оңай. Олай болса берілген теңдеудің 9 натурал шешімі бар.
Жаттығу есептер:
1. Теңдеудің бүтін шешімдерін тап.
a) 
ә) 
б)
2. Теңдеудің натурал шешімдерін тап.
а)
б)
в) 
г) 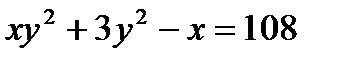

1. (2007 Жаутіков олимпиадасы) 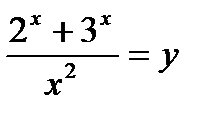 шексіз көп натурал шешімдері болатынын дәлелде.
шексіз көп натурал шешімдері болатынын дәлелде.
Нұсқау: Теңдеуді  түріне келтіріп, (1;5), (5;11) д.с пар сандар шешімдер болатынын тексеріп, алдыңғы шешімнен келесі шешімді шығарып алуға болатын рекуренттік заңдылықты тап.
түріне келтіріп, (1;5), (5;11) д.с пар сандар шешімдер болатынын тексеріп, алдыңғы шешімнен келесі шешімді шығарып алуға болатын рекуренттік заңдылықты тап.  болатынын пайдалан. Жауабы:
болатынын пайдалан. Жауабы: 
2. Бөлшек өрнектін бүтін мәнін
есептеу тәсілі
1-Есеп: 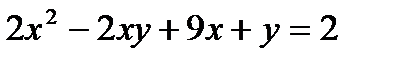 теңдеуінің бүтін шешімдерін тап.
теңдеуінің бүтін шешімдерін тап.
Шешімі: Берілген теңдеуді 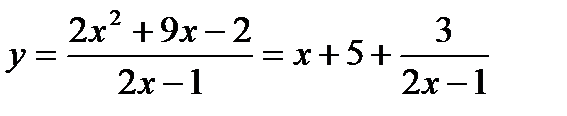 түріне келтірсек у бүтін сан болу үшін
түріне келтірсек у бүтін сан болу үшін бөлшегі бүтін мәнді қабылдау керек. Мұның төмендегі төрт мүмкіндігі бар.
а) 2х – 1 = 1, б) 2x – 1 = 3, в) 2x – 1 = - 1, г) 2x – 1 = -3. Сондықтан теңдеудің бүтін шешімдері (1; 9), (2; 8), (0; 2), (-1; 3) пар сандары болады.
2-Есеп: 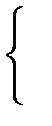
теңдеулер жүйесінің бүтін шешімдерін тап.
Шешімі: 2- теңдеуден x=y+z–3 -ті 1-теңдеуге қойсақ 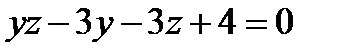 болады да
болады да 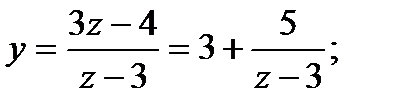 Ары қарайғы есептеу алдыңғы есеппен бірдей.
Ары қарайғы есептеу алдыңғы есеппен бірдей.
3-Есеп:  теңдеуінің натурал шешімдерін тап.
теңдеуінің натурал шешімдерін тап.
Шешімі: Берілген теңдеуді  түріне келтіруге болады.
түріне келтіруге болады.
 болатындықтан x=3, zt+1=3,
болатындықтан x=3, zt+1=3, 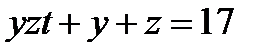 теңдіктері орындалу шарт. Бұлардан
теңдіктері орындалу шарт. Бұлардан 

 болатынын ескерсек
болатынын ескерсек 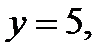
 сондықтан берілген теңдеудің натурал шешімі: (3; 5; 1; 2).
сондықтан берілген теңдеудің натурал шешімі: (3; 5; 1; 2).
4-Есеп:  теңдеуінің бүтін сандар жиынында неше шешімі бар
теңдеуінің бүтін сандар жиынында неше шешімі бар
Шешімі:  ауыстыруын орындау арқылы берілген теңдеуді
ауыстыруын орындау арқылы берілген теңдеуді немесе
 түріне келтірейік.
түріне келтірейік.
Бұдан 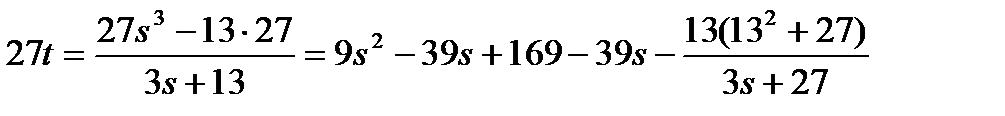 t - бүтін сан болғандықтан
t - бүтін сан болғандықтан  бүтін сан болу керек. Сондай- ақ
бүтін сан болу керек. Сондай- ақ  болатындықтан
болатындықтан 
 болады да бұдан:
болады да бұдан:
 және
және  санының осы қасиеттерге үйлесетін бөлгіштерін тапсақ: 1; 4; 7; 13; 28; 49; 52 болады да s саны сәйкес -4; -3; -2; 0; 5; 12; 13; мәндерін қабылдайды. Бұған сәйкес t-нің мәндері t = -77, -10, -3, -1; 4; 35; 42.
санының осы қасиеттерге үйлесетін бөлгіштерін тапсақ: 1; 4; 7; 13; 28; 49; 52 болады да s саны сәйкес -4; -3; -2; 0; 5; 12; 13; мәндерін қабылдайды. Бұған сәйкес t-нің мәндері t = -77, -10, -3, -1; 4; 35; 42.
x, y – тер Вьет теоремасы бойынша  теңдеуінің түбірлері болады. Бұл теңдеуді s, t – нің табылған мәндерінде шешсек (7; 5), (7; 6), (7; 12), (1; 3), (1; -1), (1; 4), (-5; 2) деген 7 шешім шығады x, y симме-триялы екенін ескерсек есептің бүтін сандар жиынында
теңдеуінің түбірлері болады. Бұл теңдеуді s, t – нің табылған мәндерінде шешсек (7; 5), (7; 6), (7; 12), (1; 3), (1; -1), (1; 4), (-5; 2) деген 7 шешім шығады x, y симме-триялы екенін ескерсек есептің бүтін сандар жиынында  шешімі болады.
шешімі болады.
Жаттығу есептер:
■■■
1. Теңдеуінің бүтін шешімдерін тап.
а) 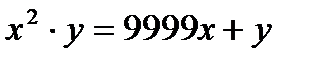 б)
б) 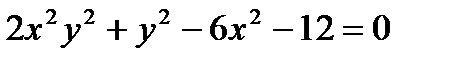
в) 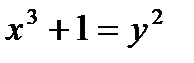 г)
г) 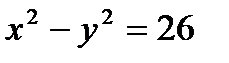
Нұсқау: «Тізбектелген екі жұп санның біреуі 2-ге, келесісі 4-ке бөлінеді де тізбектелген екі тақ сан өзара жай болатынын» және «бүтін санның k дәрежесі өзара жай сандардың көбейтіндісі түрінде жазылса осы көбейткіштердің әр қайсысы,бүтін санның k дәрежесі түрінде болады» – деген заңдылықтарды пайдалан.
г) 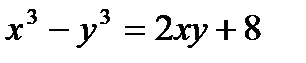 д) 3y + 11z = 60
д) 3y + 11z = 60

2. 5(xyz+x+z) = 222(yz +1) теңдеуінің натурал шешімдерін тап.
3.  cистеманың бүтін шешімдерін тап.
cистеманың бүтін шешімдерін тап.
1.5. МӘТІН ЕСЕПТЕР
1.5.1. Мәтін есептер және оны шешу туралы
Мәтін есептер өмірдегі әрқилы оқиғаларды математикалық тәуелділік түрінде тұжырымдайтындықтан оқушылардың игерген білімін өмірмен ұштастырып, қажеттілікке жаратуға дағдыланумен қатар, логикалық ойлау қабілетін жетілдіруге зор ықпал ететіндіктен, олардың математикалық дарынын жетілдіріп, ой өрісін кеңейтуде маңызды орын иеленеді.
Мәтін есептерді мазмұнына қарай: іс әрекеттік тәуелділік есептері, сандық тәуелділік есептері деп екі топқа бөлуге болады.
1. Іс әрекеттік тәуел
2. ділік есептеріне:
Әр түрлі қозғалысқа байланысты есептер, жұмыс, өнім, кіріс, шығысқа байланысты экономикалық мағаналы есептер, әр түрлі қоспалар жасау, құйу, таразылыу сияқты өлшеу есептерін жатқызуға болады.
2. Сандық тәуелділік есептеріне:
Сандардың және оның цифрларының өзара байланысына қатысты есептер,бүтін санның бөлінгіштігіне қатысты есептер, санның немесе заттың құрамы, пайызы, бөліктері, пропорцианалдық қатынастарына байланысты есептер жататын болады
Мәтін есеп шешудің ең алғашқы және ең маңызды кезеңі есептің мәтінін, қойылымын түсіну болып табылады. Біз бұл кезеңде берілген шамалар не?, белгісіз шамалар немесе табатынымыз не?, бұлар өзара қандай шартпен байланысқан немесе қандай тәуелділік берілді? деген маңызды сұрақтарға жауап іздеу арқылы есептің құрылымына толық талдау жасап, есептің мәтіні арқылы берілген тәуелділікті математикалық тәуелділікке келтіруіміз керек. Бұл кезеңнен табысты өте алсақ шығарылу жолын таңдау, шешім жасау кезеңдері математикалық ортақ әдіс тәсілдер бойынша өрнек немесе теңдеу құрып шешу арқылы жүзеге асатын болады.
Сондықтан да мәтін есеп шешуге дағдылану үшін есептің мағанасын жете түсініп, мазмұндық талдау жасау арқылы есеп қойылымын математикалық тәуелділік түріне келтірудің әдіс тәсілдерін жете игеруді мақсат ету қажет.
Біз төменгі мысалдар арқылы мәтіндік талдау жасауды кестені пайдаланып жүзеге асыру жолдарын түсіндіруді мақсат еттік. Келтірілген тәсіл қандай да типтің есептеріне керектенуге қолайлы, мәтінге жан жақты талдау жасуға толық мүмкіндік бере алатын, есептегі тәуелділік қарапайым кесте элементтерінің арасындағы тәуелділік түріне келіп, есепті түсінуге, оны шешудің жолын таңдауға, есептің шешімін тексеруге жан жақты қолайлы жағдай туатын деген сияқты көптеген артықшылықтарымен ерекшеленетін болады. Бұл арада ең басты мәселе есептің мағынасымен мазмұнын толық аша алатындай етіп кестенің жолдарымен бағандарын тиімді түрде таңдап алу болмақ.
Мысал-1: Ағайынды үшеуі мектептен үйге қарай бірге шығады. Үлкен ағасы ортаншысынан 2 есе, кішісінен 3 есе баяу жүреді. Кішісі үйге бұрын жетіп анасының әзірлеп қойған тортынан жей бастады да ортаншысы келгенше торттың 1/7 бөлігін жеді. Ортаншысы келісімен екеуі бірігіп бірдей 1/7 өнімділікте тортты жеген болса, үлкен ағасы үйге жеткенде торт қала ма?
Шешімі: Бұл қозғалыс және еңбек өнімділігін қатар қамтыған мағыналы есепке жатады. Есеп шартын төмендегідей кестеге келтірейік. Бұл есеп «іс әрекет тәуелділігі» есебіне жатады және ісәрекетке қатысушылар саныүш, екі ісәрекеттің әр қайсысы үш элементке тәуелді болатынын ескеріп, 5 жол, 7 бағаннан тұратын төменгі кестені таңдаймыз.
1-тәсіл:
| Іс әрекет Қатысушы | Жол жүру | Торт жеу (жұмыс) | ||||
| V | S | t1=S:V | t2 | Өнім N | Жұмыс A | |
| Үлкен ағасы | x | 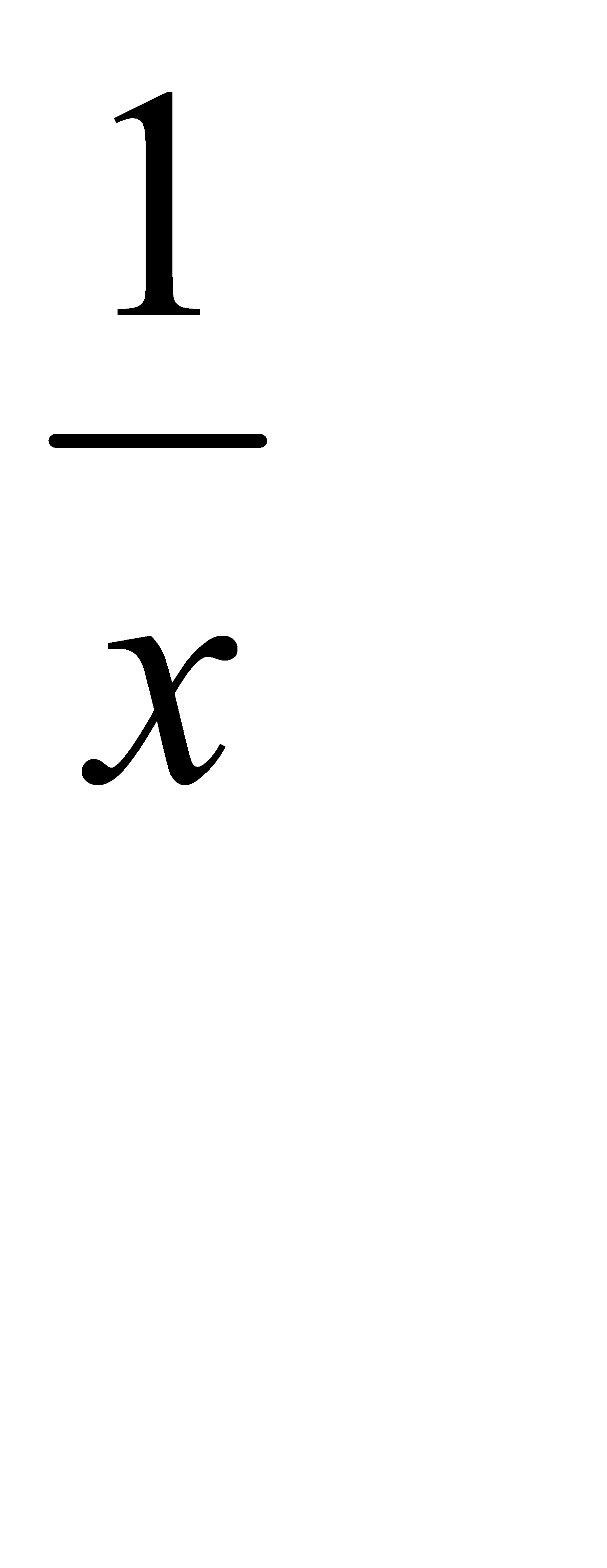
| ||||
| Ортаншысы | 2x | 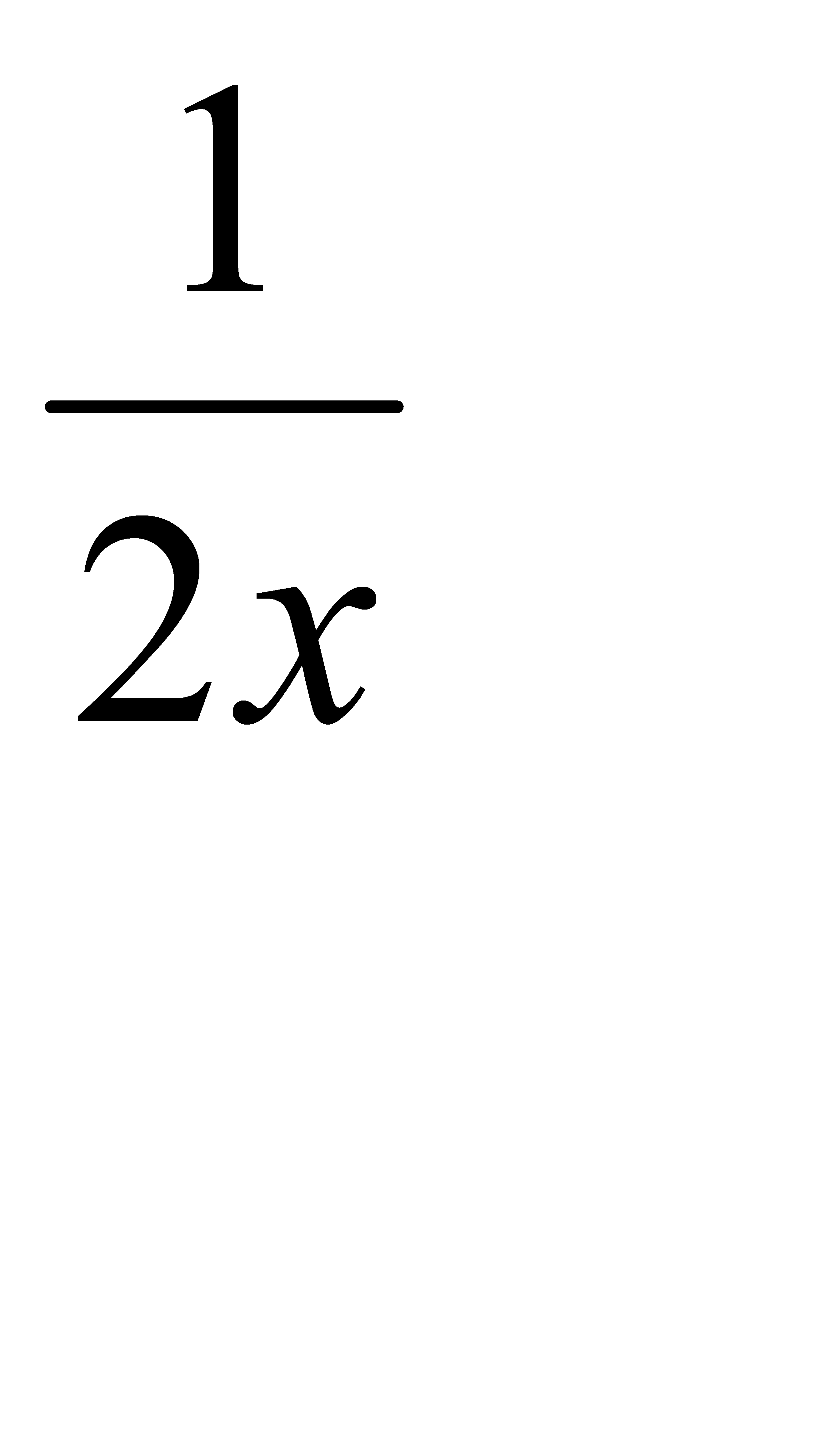
| 
| 
| 
| |
| Кіші інісі | 3x | 
| 
| 
| 
|
Торт жеу өнімі: Бұдан өнім бірлік уақытта істелетін жұмыс болғандықтан
пропорция құрсақ:  Олай болса ағасы жеткенше Ортаншысы:
Олай болса ағасы жеткенше Ортаншысы: 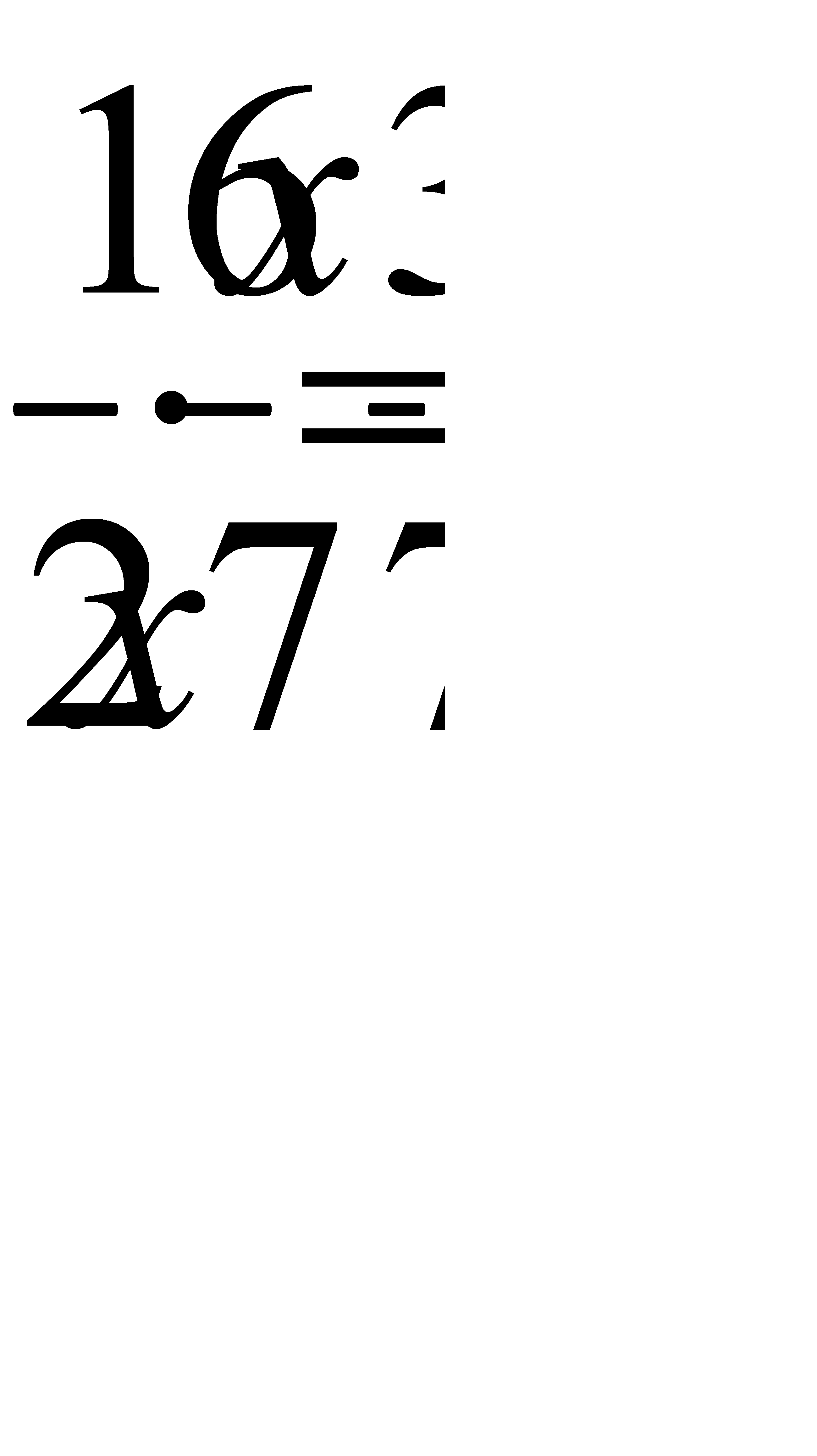 бөлік. Кішісі:
бөлік. Кішісі:  бөлік, екеуі бірігіп тортты жеп тауысады.
бөлік, екеуі бірігіп тортты жеп тауысады.
2-тәсіл: Барлық жолды 6 бөліктен тұрады, үлкен ағасының жылдамдығын 1 бірлік жылдамдық деп алсақ есепті шешуге тиімді жағдай туындайтынын пайдаланып, кестені түсініп, есепті шеш.
| Іс әрекет Қатысушы | Жол жүру | Торт жеу (жұмыс) | ||||
| V | S | t1=S:V | t2 | Өнім N | Жұмыс A | |
| Үлкен ағасы | 
| |||||
| Ортаншысы | 6 – 3 = 3 |  
| 
| |||
| Кіші інісі | 6 – 2 = 4 | 
|  
|
Мысал-2: Пішеншілер бригадасы біреуі біреуінен 2 есе үлкен екі алаңды шабуға шықты. Түстен бұрын олар үлкен алаңда жұмыс жасады. Түстен кейін олар тең екі бөлікке бөлініп, жартысы үлкен алаңың, жартысы кіші алаңның шөбін шаппақ болды. Кешке жұмыстан түскенде олар үлкен алаңды шауып бітіріп, кіші алаңнан бір жұмысшы бір күнде шабатындай алаң қалған болса бригада неше адамнан тұрады.
Шешімі: Адамдар санын х деп алып, еңбек өнімділігі адамдар санымен өлшенетінін ескеріп, кесте құрсақ:
| Кезеңі Жұмыс бөлігі | Үлкен алаң | Кіші алаң | ||||
| Уақыт t | Өнім N | Жұмыс A | t | N | A | |
| Түстен бұрын | 0,5 (күн) | х (адам) | 0,5х | = | = | = |
| Түстен кейін | 0,5 (күн) | 0,5х | 0,25х | 0,5 (күн) | 0,5х | 0,25х |
| Барлық | 1 күн | 0,75х | 0,5 күн | 0,25х |
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2058; Нарушение авторских прав?; Мы поможем в написании вашей работы!