Немесе комбинаторика 3 страница

1.3. БҮТІН САННЫҢ БӨЛІНГІШТІК ҚАСИЕТТЕРІ

1.3.1. Жай және құрама сандар

Теорема 1. Кез келген құрама санды жай сандардың көбейтіндісіне бір мәнді жіктеуге болады.

Дәлелдеме: m 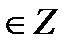құрама саны анықтама бойынша 1 < m₁; m₂ < m, 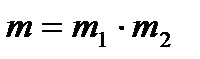түрінде жазылады. m₁ ; m₂-лерде құрама сан бар болса ол тағы өзі және бірден өзге екі санның көбейтіндісі түрінде жазылатын болады. Осы амалды қайталау арқылы барлық көбейткіштерді жай сан түріне келтіре аламыз.

m-саны шектеулі бүтін сан болғандықтан көбейткіштерге жіктеу амалы шектеусіз жалғасу мүмкін емес екені түсінікті. Жай көбейткішке жіктеу нәтижесінде m саны жай сандардың дәрежелерінің көбейтіндісі түрінде жазылатын болады.

Мысал-1: 420 және 884 сандарын жай көбейткіштерге жікте. Бұл сандардың әр түрлі неше бөлгіші болатынын есепте.

420 = 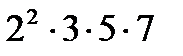, 884= 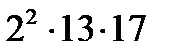түрінде жіктелумен қатар 420-ның бөлгіштерінің саны 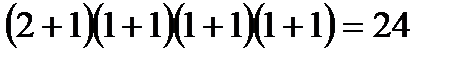, сол сияқты 884-тің бөлгіштерінің саны 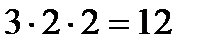болатынын жай көбейткіштердің бөлгіштер құрамына кіретін дәреже-лерін есептеу арқылы табу керек. Бұдан санның жай жіктелуін пайдаланып қанша бөлгіші болатынын табу үшін жай жіктелудегі көбейткіштердің дәреже көрсеткіштерін бірмен арттырып өзара көбейту қажет. Себебі р- жай саны үшін 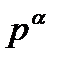-ның 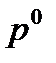, , 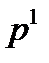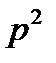… 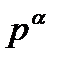деген α+1 болатыны белгілі.

Немесе: n саны 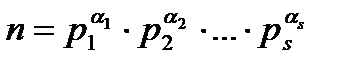түрінде жай көбейт-кішке жіктелген болса n-нің барлық бөлгіштерінің саны төменгі формула бойынша есептеледі: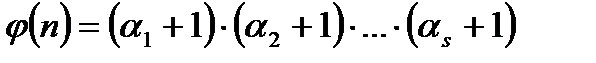

Теорема-2 Егер m саны құрама сан болса оның жай көбейткіштерінің ішінен 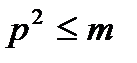болатын р-жай саны табылады.

Дәлелдеме: Кері жору тәсілін қолданайық. Немесе m-құрама санның барлық жай көбейткіштері үшін 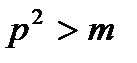болады деп көрейік m – құрама сан болғандықтан оның кемінде 2 жай көбейткіші болады. Оларды p₁, p₂ десек кері жору бойынша 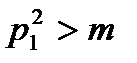, 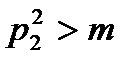яғни 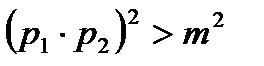немесе 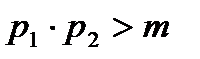. Бұлай болуы мүмкін емес ( 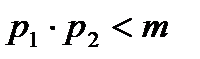болу шарт).

Мысал-2: 667; 113 сандары құрама әлде жай сан екенін анықта.

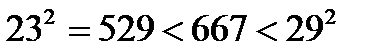(23-тен кейінгі жай сан 29) болатындықтан 667 саны құрама сан болса 23-тен артпайтын жай көбейткіші болу керек. 667-ні 23-ке дейінгі жай сандарға бөлу арқылы бұған көз жеткіземіз. 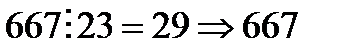құрама сан 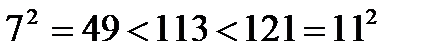және 113 саны 7-ге дейінгі жай сандар 2; 3; 5; 7-лердің қайсысына да бөлінбейді сондықтан 113 жай сан.

Жаттығу есептері:

1. 2240, 1782 сандарын жай көбейткішке жіктеп, барлық бөлгіштерінің санын тап.

2. 100-ге дейінгі сандардың ішінен айырмасы жай сан болатын пар жай сандарды тап. (Мысалы: 5 – 2 = 3) Тұжырым жаса.

3. m > n және m жұп, n тақ болса төменгі өрнектердің тақ жұптығын анықта. 5m+n, (m–n)(m+n), , , .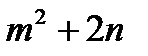

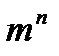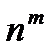4. Слава алғашқы n натурал санды, ал Валера алғашқы m жұп санды көбейткенде нәтиже бірдей шықты. Бұл екеуінің біреуі қателескенін дәлелде. ().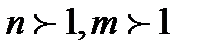

5. 1-ден 20-ға дейінгі сандардың көбейтіндісін жай көбейткішке жіктегенде 2 саны неше рет қайталанады? Бұл көбейтінді неше нөлмен аяқталады?

6. p, q- лер әр түрлі жай сандар болса төменгі сандардың бөлгіші нешеу?

а) p²q б) p²q³ в) 84p² q² г) p^mq^n-r

7. 1093 саны құрама сан ба?

8. a) p, p+4, p+14 б) p, p+10, p+14 сандары жай сандар болса р санын тап.

9. 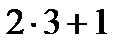, , 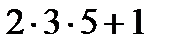, 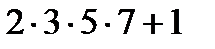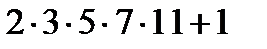сандарының қайсысы жай, қайсысы құрама сан болады? 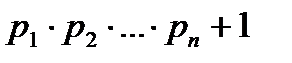саны үшін жалпы қортынды жаса. Мұндағы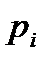 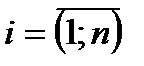саны i-ші жай сан.

10. Жай сандар шексіз көп болатынын дәлелде.

Нұсқау: 9-есептің нәтижесін пайдалан. 2-ден басталған тізбектелген жай сандардың көбейтіндісіне 1-ді қосқанда шығатын сандар тізбегін қарастыр. Тізбектің әр мүшесі не жай сан не оның құрамына енген жай сандардан үлкен жай санға бөлінуге тура келетініне көз жеткіз.

11. 2 -ден 100-ге дейінгі барлық жұп сандарды екі жай санның қосындысы түрінде жазуға бола ма? Екі жай саннның айырмасын ше?

12. 56a =65b болса a + b құрама сан болатынын көрсет (65(a + b) өрнегін бағала)

Нұсқау: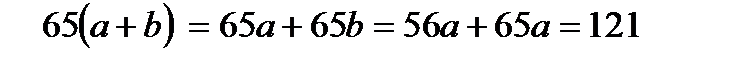

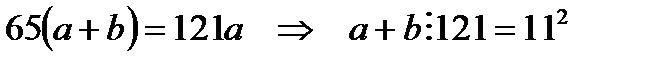
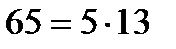
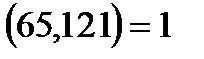
13. n+1, n+2,..., n+1000 сандарының барлығы құрама сан болатындай n-санын тап.

Нұсқау: n+1 cаны 2-ге, n+2 саны 3-ке, n+3 саны 4-ке д.с бөлінетіндей таңда. 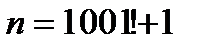деп алсақ, онда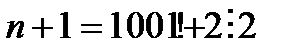 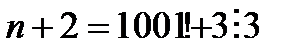д.с болатынын пайдалан.

Мұндай есептерді шешу үшін есеп шартын орындайтын қандай бір мысал табу жеткілікті.

14. 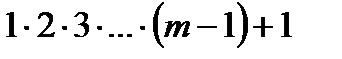саны m-ге бөлінетін болса m жай сан болатынын көрсет.

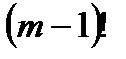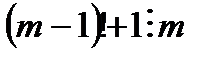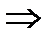
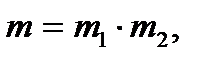
Нұсқау: m құрама сан болса cаны m-ге бөлінуге тиісті екенін дәлелдеп, есепті шешуге пайдалан. және m–құрама сан дейік. 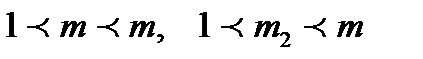. Бұдан 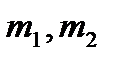сандары 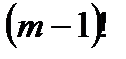-дің құрамында бар көбейткіштер 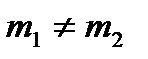кезде бұлар әр түрлі сандар 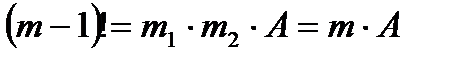немес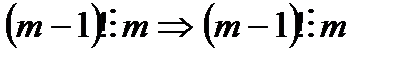е және 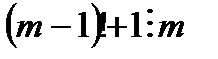бұл мүмкін емес.

15. Қосындысы мен айырмасы жай сан болатын екі жай санды тап.

16. Тізбектелген n-тақ санның қосындысы құрама сан болатынын көрсет.

Нұсқау: 1-ден бастап (2n-1)-ге дейінгі n сан үшін дәлелдесек жеткілікті

n=2 1+3 = 4= 2²

n=3 1+3+5= 9= 3²

n=4 1+3+5+7 = 16 = 4²

1+3+5 +7+9 = 25 = 5²

.

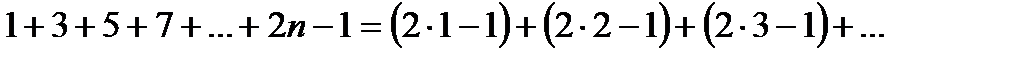
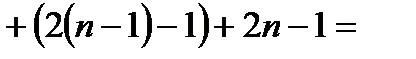
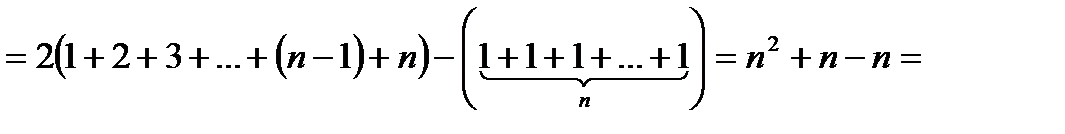
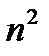17. Жазылуында барлық 10 цифр бір бір рет кірісетін 36-ға бөлінетін ең кіші және ең үлкен санды тап.

Нұсқау: Бұл санды А деп белгілесек: 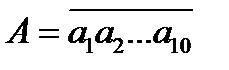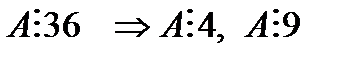A санының цифрларының қосындысы 45-ке тең болғандықтан бұл сан 9-ға бөлінеді. Ал 4-ке бөліну үшін соңғы 2 цирдан тұратын сан 4-ке бөліну қажет.

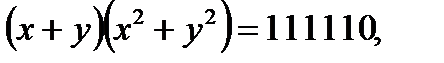
18. 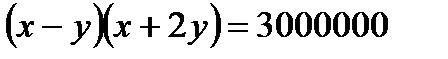, 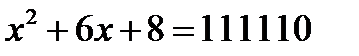теңдеулерінің бүтін шешімдері бола ма?

Нұсқау: 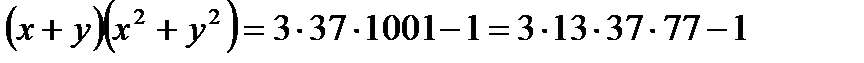болатынын ескеріп қорытынды жаса.

19. а) 7 бөлгіші болатын жұп санды тап.

б) 10 бөлгіші болатын 12-ге бөлінетін санды тап.

Нұсқау: 26-бет мысал-1-дің қорытындысын пайдалан.

1.3.2. Бөлінгіштік белгілері мен қасиеттер

a) Бөлінгіштік белгілері

Төмендегі бөлінгіштік белгілерін дәлелде:

1. Жұп сан 2-ге бөлінеді.

2. Санның цифрларының қосындысы 3-ке (9-ға) бөлінсе бұл сан 3-ке (9-ға) бөлінеді. (Санның цифрларының қосындысын 3-ке (9-ға) бөлгенде қалған қалдық сол санды 3-ке (9-ға) бөлгендегі қалдыққа тең.)

3. Санның соңғы екі (үш) цифрынан құралған сан 4-ке (8-ге) бөлінсе бұл сан 4-ке (8 -ге) бөлінеді.

4. 0 және 5-пен аяқталған сан 5-ке бөлінеді.

5. Натурал санның соңынан бастап үш үш цифрдан бөліктерге бөліп (ең сол жаққы бөлік 3-тен аз цифрмен жазылған болуға болады) тақ реттегі бөліктерді қосу таңбасымен жұп реттегі бөліктерді алу таңбамен алғанда шығатын қосынды 7-ге (13-ке, 11-ге) бөлінсе бұл сан 7-ге (13 ке, 11-ге) бөлінеді.

6. Натурал санды соңынан екі екі цифрдан тұратын бөліктерге бөліп, (ең сол жақ бөлік бір цифрдан тұруға болады) шыққан сандарды қосқанда 11-ге бөлінсе бұл сан 11-ге бөлінеді.

7. Жұп орындағы цифрлардың қосындысы мен тақ орындағы цифрлардың қосындысының айырмасы 11-ге бөлінсе сан 11-ге бөлінеді.

Мысалы 1. 237849568 саны а) 11-ге бөліне ме?

б) 2-ден 13-ке дейінгі сандардың қайсысына бөлінеді егер бөлінбесе оған ең жақын бөлінетін санды тап.

в) 2-ден 13-ке дейінгі сандардың бәріне де бөлінетін берілген санға ең жақын санды тап.

Нұсқау: а) 68+95+84+37+2=286 белгіні қайта керектенсек

86+2=88,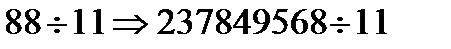

Мысалы 2. 459348965866 саны 7-ге, 13-ке бөліне ме?

459-348+965-866=210 алғашқы сан 7-ге бөлінеді де13-ке бөлінбейді.

b) Бөлгіштік қасиеттері

Төмендегі бөлінгіштік қасиеттерін дәлелде:

1. a cаны b-ге бөлінсе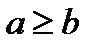

2. a cаны b-ге, b саны а-ғе бөлінсе a = b

3. a cаны b-ге, b саны с-ге бөлінсе, а саны с-ге бөлінеді.

4. a; b сандары с-ге бөлінсе, кез келген натурал m,n үшін ma+nb саны с-ге бөлінеді. Және де ma > mb болса ma – nb cаны с-ге бөлінеді.

5. а саны b-ге бөлінсе кез келген натурал k үшін ak саны b-ге бөлінеді.

6. ak cаны bk-ға бөлініп, 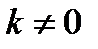болса а саны b-ге бөлінеді.

7. 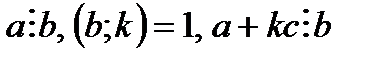шарттары орындалса .

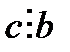8. 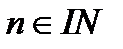болса 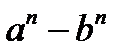саны a – b -ге, n тақ сан болса 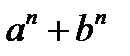cаны а + b-ге бөлінеді.

Жаттығу есептер:

1. 10-ға, 15-ке бөлінгіштік белгісін тап.

2. 2, 3, 5-ке қатар бөлінетін 5 сан жаз.

3. 9-ға бөлінетіндей етіп *-ның орнындағы цифрды тап.

3474*7, 123*75, 475*286

4. 3 пен 2-ге қатар бөлінетіндей етіп * - ның орнына цифр жаз.

3684* 572*, 746**

5. 2, 5, 25, 4, 8, 7, 9, 11, 13-ке (жеке жеке) бөліну үшін 23857* cанның соңғы цифры нешеу болады?

6. 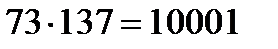теңдігін пайдаланып 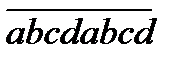cаны 73 және 137-ге бөлінетінін көрсет.

Нұсқау: 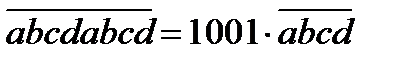теңдігі орындалатынын көрсет.

7. 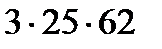санның барлық бөлгіштерін тап. Оларды өсу ретімен орналастыр. Барлық көбейткіштердің көбейтіндісіне 2-нің, 3-тің, 5-тің неше дәрежесі кіріседі?

8. а-саны 6-ға бөлінсе a(a-12) cаны 36-ға бөлінетін көрсет.

9. 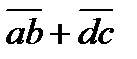саны 9-ға бөлінсе 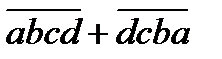cаны 99-ға бөлінетінін дәлелде.

10. 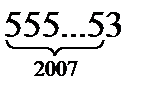саны құрама сан болатынын көрсет.

11. Төменгі шарттарды қанағаттандыратындай (x; y) пар санының үш мәнін тап. 12x + 45y cаны

a) 2-ге бөлінеді.

б) 5-ке бөлінеді.

в) 2 және 5-ке бөлінеді.

г) 2-ге де 5-ке де бөлінбейді.

12. 100 дана 0, 100 дана 1, 100 дана 2 цифрларын пайдаланып бүтін квадрат болатын сан жазуға бола ма?

Нұсқау: Мұндай сан 3-ке бөлінгенімен 9-ға бөлінбейтінін және санның квадраты 3-ке бөлінсе 9-ға бөлінуі шарт екенін ескер.

13. Бүтін санның 6-ға, 18-ге, 33-ке, 12-ге, 50-ге, 37-ге, 111-ге бөліну белгісін анықта.

Нұсқау: 33-ке бөліну үшін 3-ке және 11-ге қатар бөлінуі қажет. 37-ге, 111-ге бөліну белгісі үшін 1000-1=999=9∙3∙37 теңдігін пайдалан.

14. Кез келген санның квадраты не 9-ға бөлінеді, не 3-ке бөлгенде 1 қалдық қалатынын дәлелде.

15. 1-ден 300-ге дейінгі сандарды тізіп жазғанда шыққан сан 3-ке бөлінетінін дәлелде. Бұл сан 9-ға бөліне ме? Басқа қандай сандарға бөлінетінін анықта.

16. a+b саны 7-ге бөлінсе 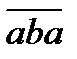cаны 7-ге бөлінетінін көрсет.

17. 1-ден 100-ге дейінгі сандардың ішінде 3-ке бөлін-генімен жазылуында 3 цифры болмайтын сан нешеу?

18. 1-ден 9-ға дейінгі сандарының бәріне де бөлінетін а) 2007-мен басталатын ең кіші б) 2008-бен басталатын ең кіші, в) 2009-бен басталатын ең кіші санды тап.

Нұсқау: а) Бұл сан 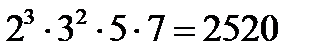-ға бөлінумен қатар 2008-бен басталатын онымен бірдей таңбалы саннан кіші болатынына көз жеткізіп, 200800.... түріндегі санды 2520-ға бөліп, әр қадам сайын бөлінгіш пен қалдықтың айырмасын есептеп қортынды жасау тәсілін қолдан.

19. 4-ті азайтқанда 3-ке, 3-ті азайтқанда 2-ге, 4-ті қосқанда 5-ке, 5-ті азайтқанда 4-ке, 5-ті қосқанда 6-ға, 6-ны азайтқанда 5-ке, 7-ні қосқанда 8-ге, 8-ді азайтқанда 7-ге бөлінетін ең кіші санды тап.

20. Кез келген бүтін А саны үшін 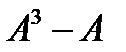, 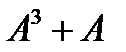екі санның кемінде біреуі 10-ға бөлінетінін дәлелде.

Нұсқау: Бұл сандардың екеуі де жұп және кемінде біреуі 5-ке бөлінетініне көз жеткізу керек.

21. Алғашқы екі цифрынан тұратын сан 2-ге, алғашқы үш цифрдан тұратын сан 3-ке, алғашқы төрт цифрдан тұратын сан 4-ке, д.с... бұл сан өзі 10-ға бөлінетіндей он әртүрлі цифрдан тұратын 10 таңбалы санды тап.

22. Тізбектелген 4 санның көбейтіндісі 3024. Осы сандарды тап.

23. 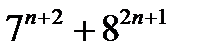саны 57-ге, 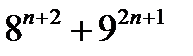cаны 73-ке бөлінетінін дәлелде.

Нұсқау: Өрнектерді түрлендіру арқылы көбейткіштерге жіктеу, нәтижесінде сәйкесінше 57 және 73 көбейткіштерін шығарып алу керек. Сондай ақ қосындымен айырмалардың бөлінгішдік қасиеттерін пайдаланау қажет.

24. n(n+1) саны 2-ге, n(n+1)(n+2) саны 3-ке бөлінетінін дәлелдеп, жалпы жағдайда тұжырымдама жаса.

Нұсқау: Тізбектелген сандардың бөлінгіштік қасиеттерін пайдалан.

25. 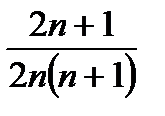бөлшегі қысқармайтынын дәлелде.

26. А санын 1981 және 1982 -ге бөлгенде 35 қалдық қалатын болса 14 -ке бөлгенде неше қалады?

27. 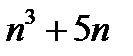саны 6-ға, 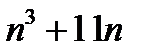саны 6-ға,

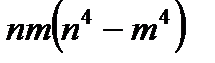саны 5-ке, 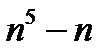саны 30-ға, 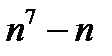саны 7-ге бөлінетінін дәлелде.

28. 1000!= cаны неше нольмен аяқталады?

Нұсқау: 1000! cанның құрамындағы 5- көбейткіші мен есеп шартының ара байланысын анықта. 29-есептің мазмұнын пайдалан. Ол үшін p=5 деп ал.

29. n!-ді бөлетін p-нің ең үлкен дәрежесі 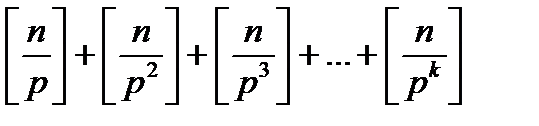(*) болатынын дәлелде. Мұнда k- саны 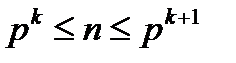теңсіздігін қанағаттандыратын натурал сан да 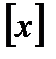x-санының бүтін бөлігі(х-тен артық емес ең үлкен бүтін сан).

Нұсқау: n= 12; 100, p = 5; 8 жағдайларда есепті шешіп, жалпы жағдайда қорытынды жаса. p = 5 кезде (*) өрнектің мәні n!= 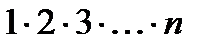көбейтіндісі неше нөлмен аяқталатынын айқындайтынына көз жеткіз.

30. 5-пен көбейткенде цифрларының қосындысы өзгермейтін сан 9-ға бөлінетінін дәлелде.

Нұсқау: 5A – A = 4A теңдігін және цифрларының қосындысы тең сандардың айырмасы 9-ға бөлінетініне көз жеткізіп пайдалан.

31. Кез келген тізбектелген 18 үш таңбалы санның кемінде бірі өз цифрларының қосындысына бөлінетінін дәлелде.

Нұсқау: 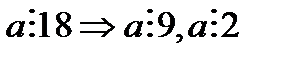және кез келген тізбектелген k санның біреуі k-ға бөлінетінін пайдалан. 9-ға бөлінетін үш таңбалы санның цифрларының қосындысының мүмкін мәндерін ескер.

32. а) Әр түрлі 7 цифрдан тұратын, барлық цифрларына бөлінетін 7 таңбалы санды тап.

б) Әр түрлі 8 цифрдан тұратын, барлық цифрларына бөлінетін 8 таңбалы сан табылмайтынын дәлелде.

Нұсқау: а) Алдымен есептің шартын қандай цифрлар қанағаттандыратынын анықта, мәселен 0 және 5 цифрлары кіре ме? Санның 9-ға бөлінгіштік белгісін ескер. б) 0 және 5-тен басқа 8 цифрдан жазылған 8 таңбалы сан 9-ға бөліне ме?

33. 2; 3;...; 9 цифрларын бір бір рет қана пайдаланып екі сан жазылған. (Мысалы: 672 және 58943) жазылған екі санның біреуі екіншісінен 2 есе үлкен болуы мүмкін бе?

Нұсқау: Бір бірінен 2 есе үлкен екі санның қосындысы (x + 2x = 3x саны) қандай санға бөліну керек екенін анықта. Санның 3-ке бөлінгіштік белгісін пайдалан.

34. 1-мен өзінен басқа бөлгіштерінің ең үлкені ең кішісінен 25 есе үлкен болатын барлығы неше натурал сан болады?

Нұсқау: Сан ең кіші және ең үлкен көбейткіштерінің көбейтіндісіне тең болатынын және есеп шартын ескеріп теңдеу құр. Жауабы 3 сан.

35. S(x)-пен х санының цифрларының қосындысын белгілейік. Төменгі теңдеулерді шеш.

а)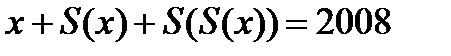

б)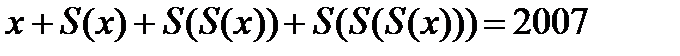

в) б)-нің 2007-нің орнына 2005-ті қой.

Нұсқау: Сан және оның цифрларының қосындысын 3-ке (9-ға) бөлгенде бірдей қалдық қалатынын пайдалан.

в) 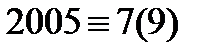болғандықтан теңдіктің сол жағындағы әр қосылғышты 9-ға бөлгенде бірдей 4 қалдық қалу керек болатынын анықта.

36. Цифрларының қосындысынан 83 есе үлкен болатын 4 таңбалы санды тап.

Нұсқау: Бұл төрт таңбалы санды х десек x – S(x) саны 9-ға және 82-ге бөлінетінін көрсет.

Дата добавления: 2014-12-16