Карно теоремасы 1 страница

Теорема - 4: Үшбұрыш қабырғаларының орта перпенди-кулярлары бір нүктеде қиылысады. Бұл нүкте сырттай сызылған шеңбердің центрі болады.

Дәлелдеме: Кесіндінің орта перпендикуляры кесінді ұштарынан бірдей қашықтықта жататын нүктелердің геометриялық орны болатынынан теореманың дәлелдемесі оңай шығады.

Теорема 5: (Карно теоремасы)

АВС үшбұрышының АВ, ВС, СА қабырғаларындағы сәйкес С₁, A₁, B₁ нүктелерінен үшбұрыш қабырғаларына жүргізілген үш перпендикуляр бір нүктеде қиылы-суының қажетті және жеткілікті шарты 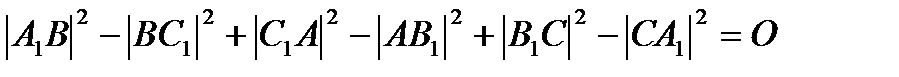болып табылады.

Дәлелдеме: А_1; В_1; С₁ нүктесінде қабырға тұрғызылған перпендикуляр М нүктесінде қиылысатын болса |ВМ|² - |ВА₁|² = |МС|² - |А₁С|² = |МА₁|² болатын-дықтан |ВМ|² - |МС|² = |ВА₁|² - |А₁С|₂ (1) болады сол сияқты |МС|²-|МА|²=|АВ₁|²-|В₁С|² (2)

| МА|² - |МВ|² = |АС₁|² - |С₁В|² (3).

(1), (2), (3) теңдіктерді қоссақ

|А₁В|² - |ВС₁|² + |С₁А|² - |АВ₁|² + |В₁С|² - |СА₁|² = 0 болады.

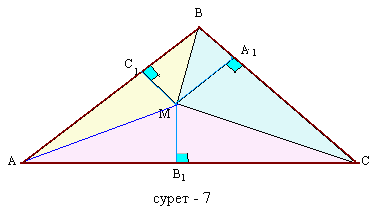
Енді теореманың кері қортындысын немесе теңдік орындалатын жағдайда А₁; В₁; С₁ нүктелері М нүктесінен қабырғаларға жүргізілген перпендикуляр-лардың табан-дары болатынын дәлелдейік.

А₁; С₁ нүктелерінен жүргізілген перпендикуляр-лардың қиылысу нүктесін М – десек

|МА|² - |МВ|² = |С₁А|² - |ВС₁|²,

|МВ|² - |МС|² = |А₁В|² - |СА₁|² болады да теореманың шарты болушы теңдікке нәтижені қойсақ |МА|² - |МС|² = |АВ₁|² -|В₁С|² болатындықтан В₁ нүктесі М -нен жүргізілген перпендикулярдың табаны болатыны көрініп тұр.

Бұл М нүктесін Карно нүктесі деп те атайды.

Жаттығу есептер:

3-1. АВС үшбұрышына сырттай сызылған шеңбердің центрі О, радиусы R, іштей сызылған шеңбердің радиусы r, О нүктесінен АВ, ВС, СА қабырғаларына түсірілген перпендикулярлардың табандары сәйкес С₁, А₁, В₁ болса:

a) Берілген үшбұрыш сүйір бұрышты болған жағдайда |ОА₁| + |ОВ₁| + |ОС₁| = R + r;

б) Егер А бұрыш доғал болса |ОВ₁|+|ОС₁| - |ОА₁| = R + r теңдігі орындалатынын дәлелде.

3-2. АВС үшбұрышының бұрыштарының биссектрисаларының созындысы үшбұрышқа сырттай сызылған шеңберді сәйкес А₁, В_1,, С₁ нүктелерінде қиюмен қатар үшбұрышқа іштей сызылған шеңбердің центрі М болса

а) 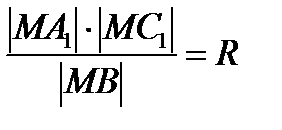б) 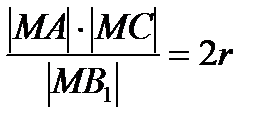болатынын дәлелде.

3-3. АВ, ВС, СА түзулеріне сәйкес С₁, А₁, В₁ нүктелерінен жүргізілген перпендикулярлар бір нүктеде қиылысатын болса А₁С₁, С₁В₁, В₁А₁ түзулеріне сәйкесінше В, А, С нүктелерінен жүргізілген перпендикулярлар да бір нүктеде қиылысатынын дәлелде.

3-4. АВСD төртбұрышының ВСD, АСD, АВD үшбұрышының биіктіктерінің қиылысқан нүктелерін сәйкесінше А₁, В₁, С₁ десек В₁С₁, С₁А₁, А₁В₁ түзулеріне А; В; С нүктелерінен түсірілген перпендикулярлар бір нүктеде қиылысатынын дәлелде.

§4. Ортоцентр және биіктіктің қасиеті

Анықтама: Үшбұрыштың төбесінен қарсы жатқан қабырға жататын түзуге түсірілген перпендикуляр-ларды үшбұрыштың биіктігі дейді.

Теорем -6: Үшбұрыштың үш биіктігі бір нүктеде қиылысады (Бұл нүктені ортацентр деп атайды)

Дәлелдеме: Берілген үшбұрыштың төбелері қабырға-ларының орта нүктесі және биіктіктері қабырғаларының орта перпендикуляры болатындай етіп, А₁В₁С₁ үшбұ-рышын салайық: (сурет-8)

Алғашқы үшбұрыштың биіктіктері салынған А₁В₁С₁ үшбұрышының қабырғаларының орта перпендику-лярларының қиылысуы, немесе А₁В₁С₁ үшбұрышына сырттай сызылған шеңбердің центрі болып, теорема дәлелденеді.

Қасиет-1. АВС үшбұрышына А, В, С төбелерінен түсірілген биіктіктердің табанын сәйкесінше Н₁, Н₂, Н₃, ортацентрді Н десек АН₂НН₃, ВН₁Н₃Н, СН₁НН₂, АВН₁Н₂ төртбұрышына сырттай шеңбер сызылады.

Дәлелдеме: а) АВС сүйір бұрышты үшбұрыш болса аталған үшбұрыштардың әрқайсында қарама-қарсы жатқан 2 тік бұрыш болатындықтан теорема дәлелденеді.

б) Доғал бұрышты үшбұрыш үшін де дәлелдеме осымен бірдей.

Қасиет-2: АВС, АН₂Н₃, ВН₁Н₃, СН₂Н₁ үшбұрыштары ұқсас болады.

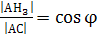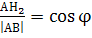, және φ бұрышы АВС, АН₂Н₃ үшбұрыштарына ортақ болатындықтан АВС, АН₂Н₃ үшбұрыштары ұқсас, ұқсастық коэффициенті 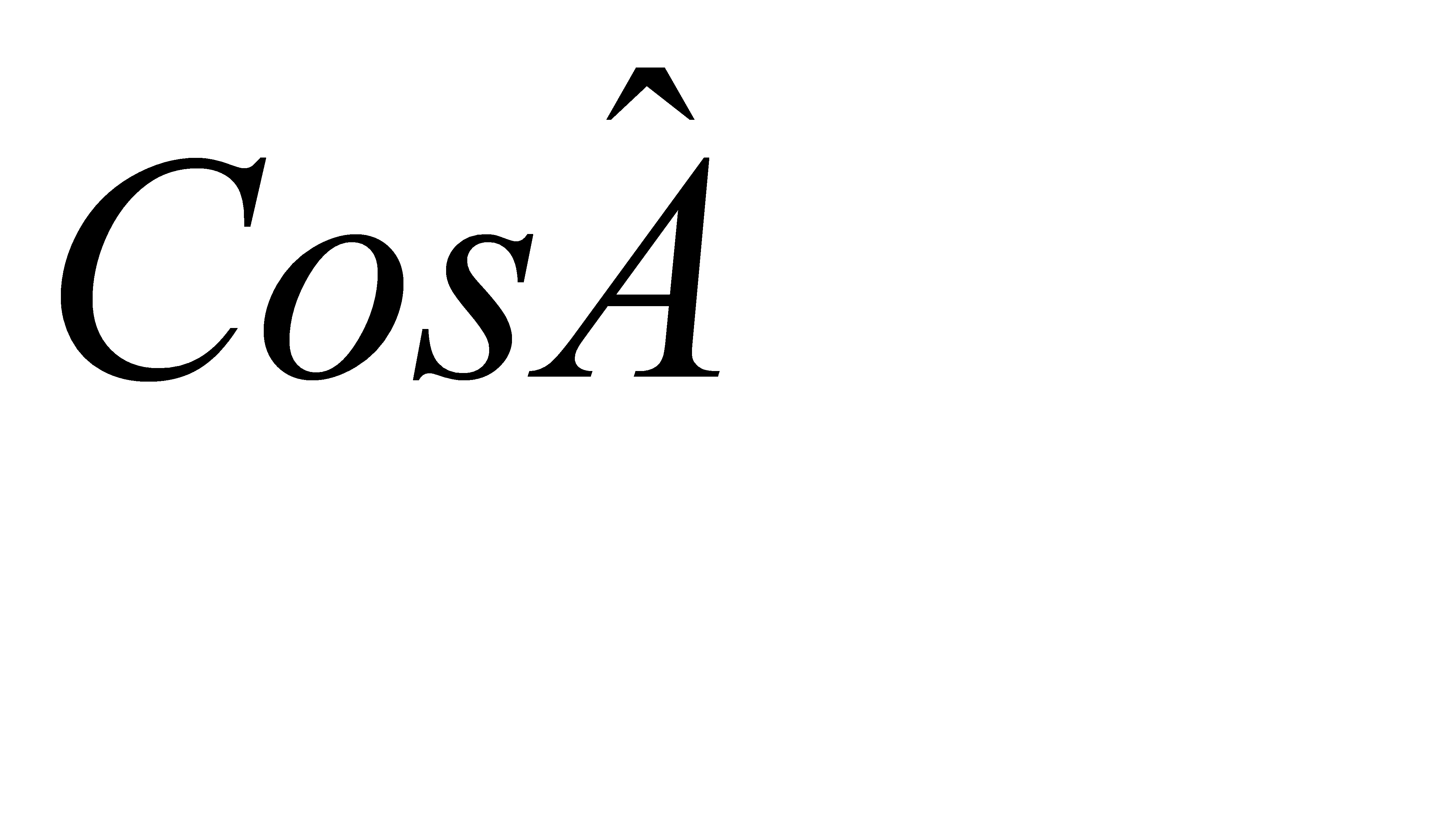– ға тең болатыны дәлелденеді.

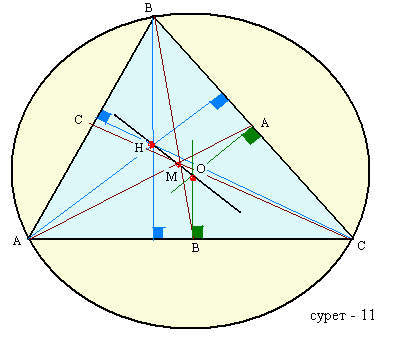
Қасиет-3: Үшбұрышқа іштей сызылған шеңбердің центрі О, ортацентр Н, ауырлық центрі М болса бұл үш нүкте бір түзудің бойында жатады да М нүктесі ОН кесіндісін 1 ׃ 2 қатынасында бөледі. (Бұл түзуді Эйлер түзуі деп Швейцарияның атақты математикші Леонард Эйлердің (1707-1783) атымен атайды)

Дәлелдеме: АВС үшбұрышының А, В төбесінен жүргізілген медианалардың табанын А₁, В₁ деп белгілейік. Центрі М, коэффициенті – 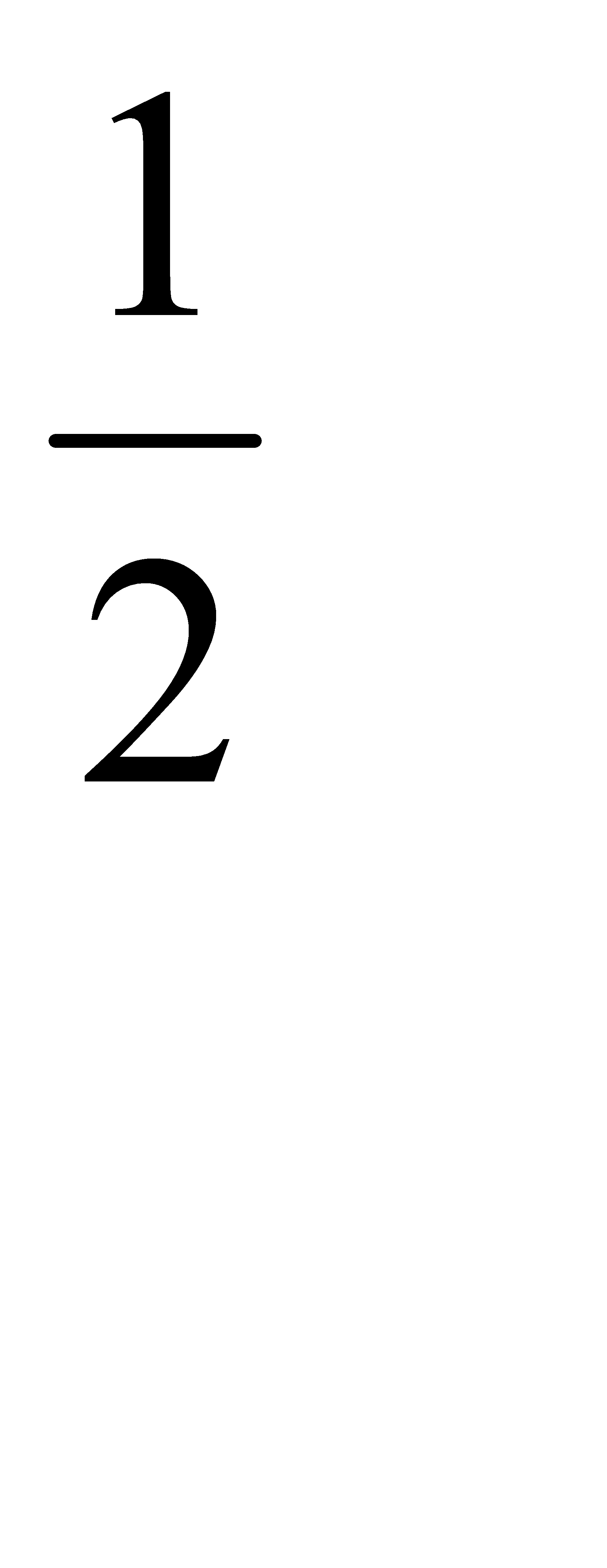болатын гомотет арқылы:

Медиананың қасиеті бойынша , 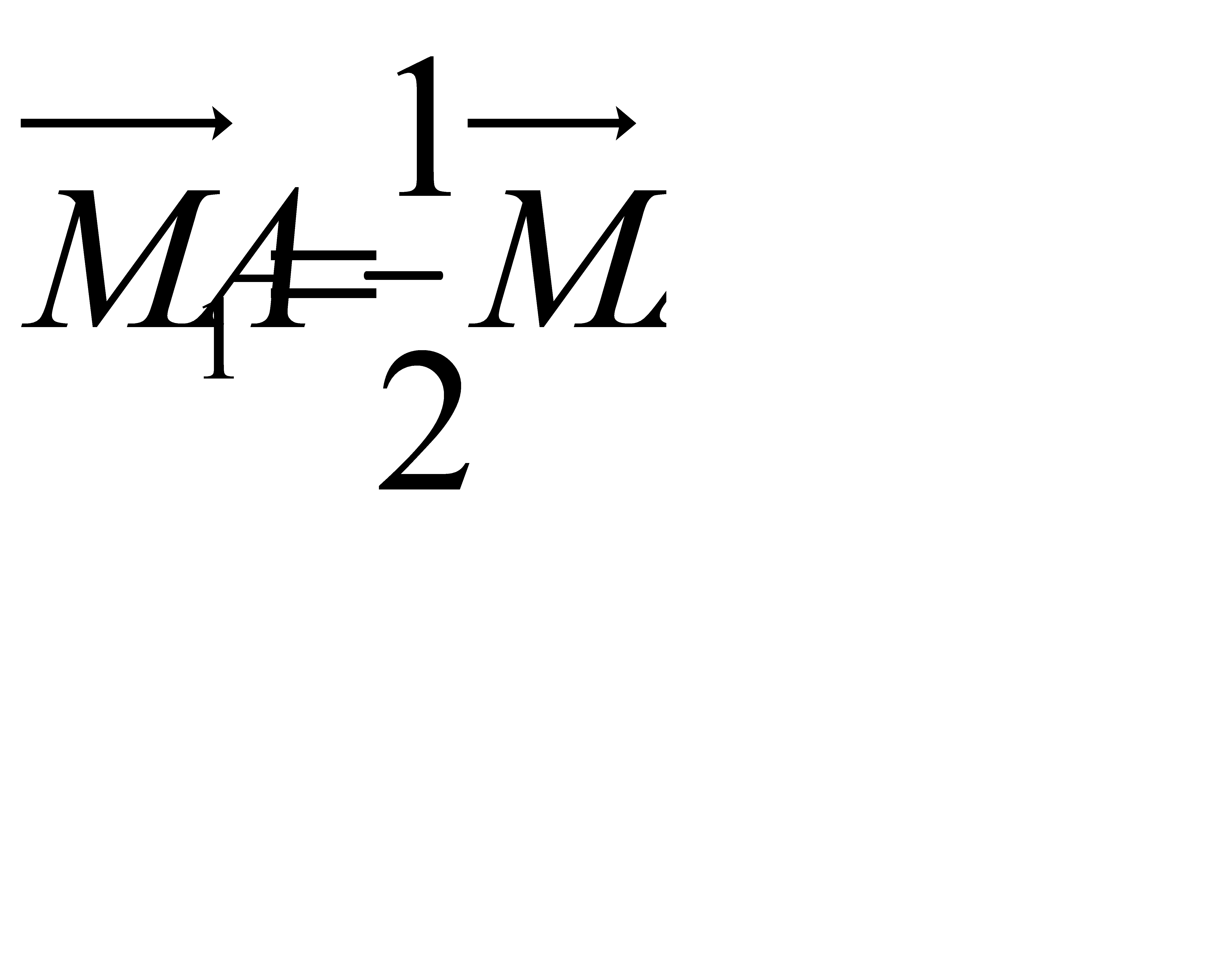болатындықтан бұл гомотет бойынша А нүктесі А₁ -ге, В -нүктесі В₁ -ге, гомотеттің қасиеті бойынша түзу оған параллел түзуге көшетіндіктен АН, ВН түзулері сәйкес А₁О, В₁О түзулеріне көшетінін байқасақ, Н нүктесі О нүктесіне ауысады. Олай болса немесе Н, М, О нүктелері бір түзуде жатады, және болып, теорема дәлелденеді.

Анықтама: Кез келген Х нүктесін 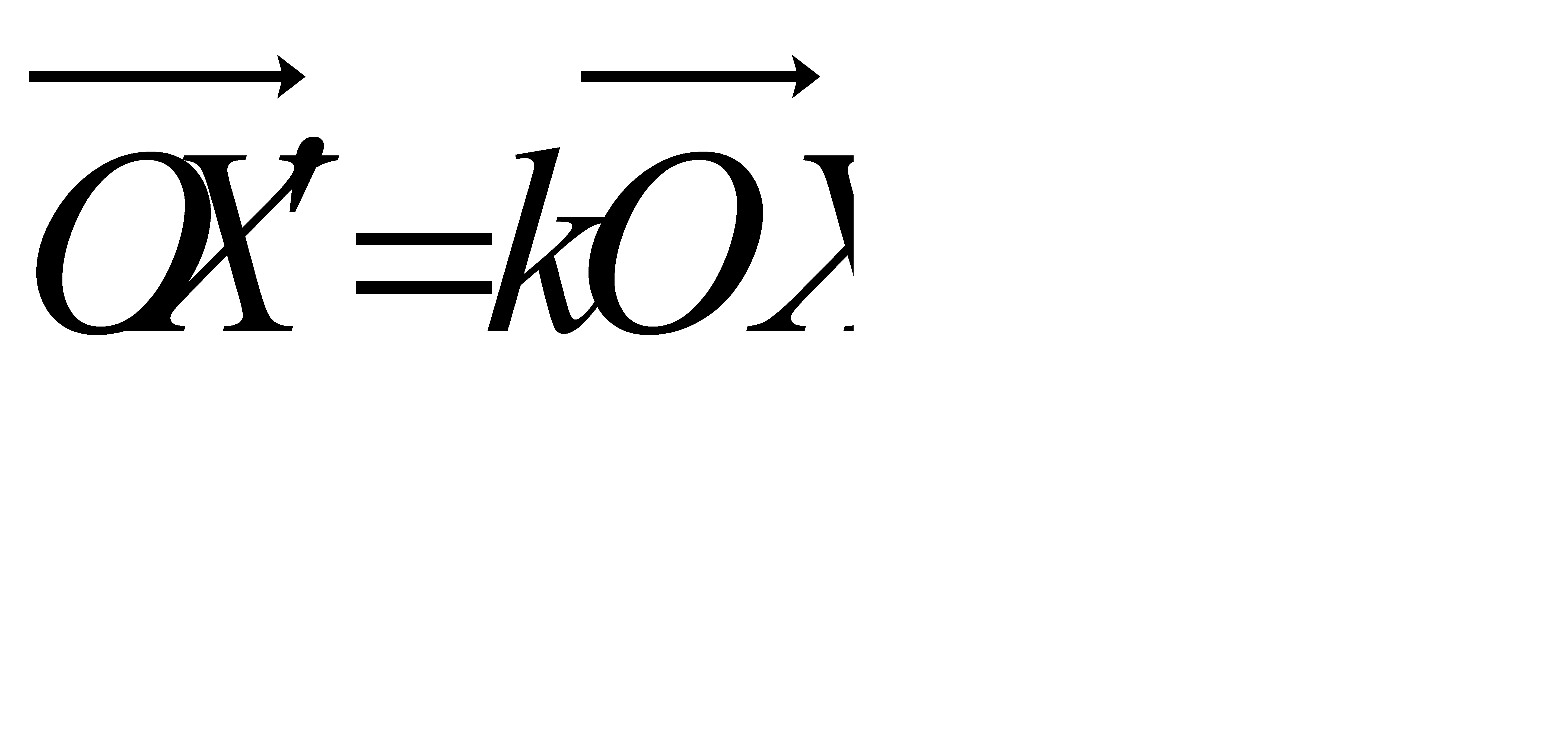заңдылығы бойынша Х' нүктесіне көшіретін «қозғалысты» центрі О, k – коэффициентті гомотетия деп атайды .

Жаттығу есептер:

4-1. АВС үшбұрышының ортацентрі С төбесінен түсірілген биіктікті 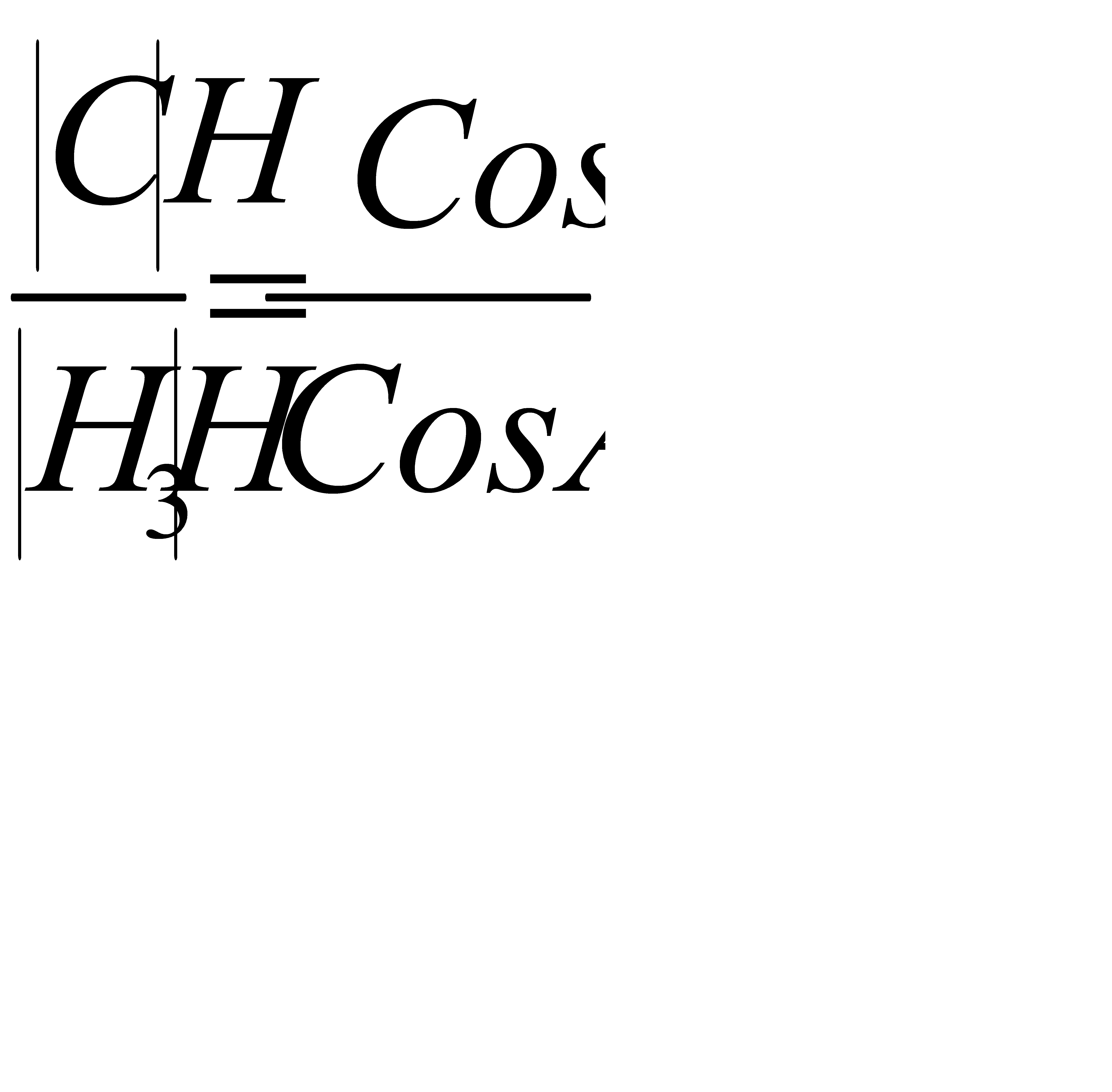қатынасында бөлетінін дәлелде.

4-2. Сүйір бұрышты АВС үшбұрышы үшін |АН|·|АН₁|+|ВН|·|ВН₂|+|СН|·|СН₃|= 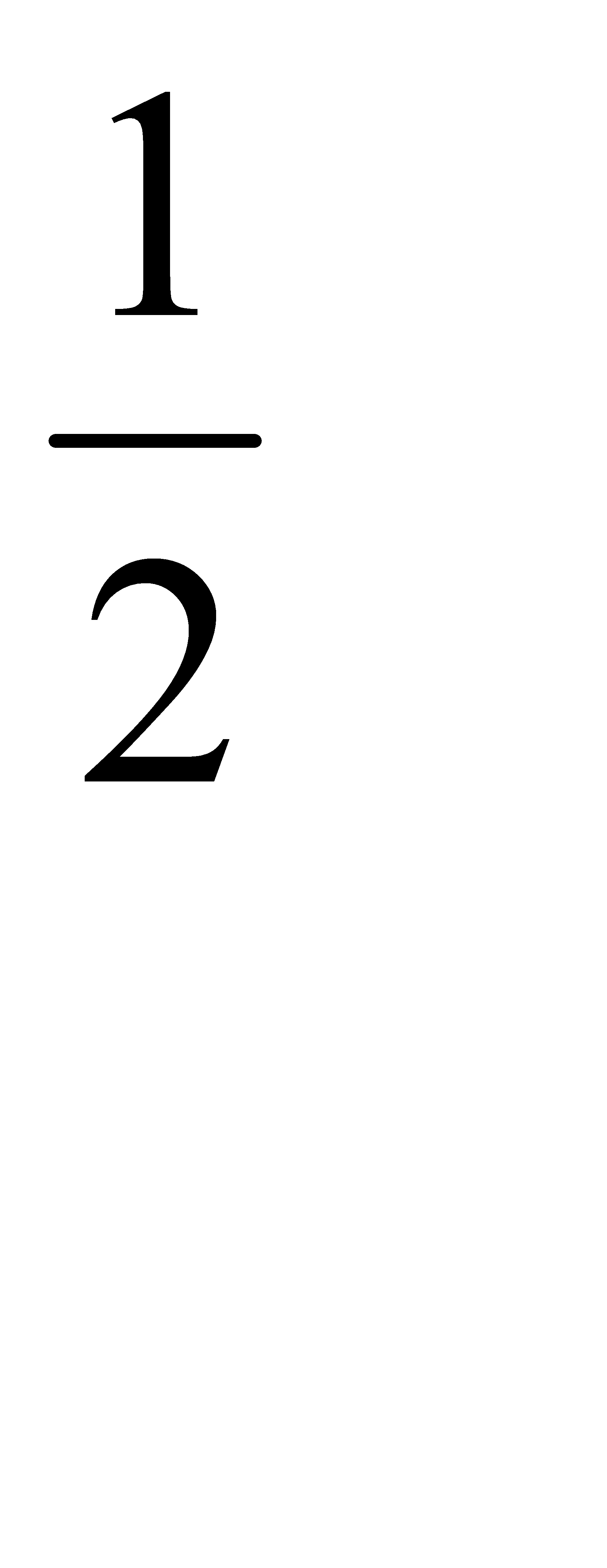(|АВ|²+ |ВС|² + +|СА|²) теңдігі орындалатынын дәлелде.

4-3. АВС үшбұрышына сырттай сызылған шеңбердің центрі О, радиусы R болса:

а) |АН| = 2R |CosA|,

б) |ОН|² = R²(1 - 8CosACosBCosС)

теңдіктері орындалатынын дәлелде.

4-4. АВС үшбұрышының А, В төбесінен түсірілген биіктіктердің табаны Н₁, Н₂ болса |Н₁Н₂| = |АВ|·CosC теңдігін дәлелде.

4-5. АВС үшбұрышының А, В, С төбелерінен түсірілген биіктіктердің ұзындығы h_a, h_b, h_c іштей сызылған шеңбердің радиусы r болса:

а) 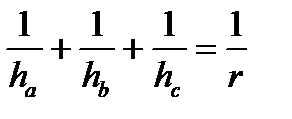б) h_a + h_b + h_c ≥ 9r болатынын дәлелде.

4-6. Доғал емес бұрышты үшбұрыштың ең ұзын биіктігі h болса R + r ≤ h теңдігін дәлелде.

4-7. Үшбұрыштың А төбесінен жүргізілген медиана m_a, биіктігі h_a, биссектриса l_а болса h_a ≤ l_a ≤ m_a теңсіздігін дәлелде.

4-8. Сүйір бұрышты үшбұрыш үшін

теңсіздігін дәлелде.

4-9. (Фаньяно есебі) Сүйір бұрышты үшбұрышқа іштей сызылған ең кіші периметрлі үшбұрыш биіктіктердің табандары төбесі болатын үшбұрыштар екенін дәлелде.

§5. Чев теоремасы мен Чевиандар қасиеті

Анықтама: Үшбұрыштың үш төбесінен шығып бір нүктеде қиылысатын үш түзуді Чев түзулері, қиылысу нүктесін Чев нүктесі, Чев түзуінің қарсы қабырғамен шектелген кесіндісін Чевиан деп атайды. Төмендегі заңдылықты Италия математигі Джовани Чев 1678 жылы ашқандықтан соның атымен аталып кеткен.

Теорем-7: АВС үшбұрышының АВ, ВС, СА қабырғалары немесе олардың созындысында сәйкесінше С₁, А₁, В₁ нүктелерін белгілесек; АА₁, ВВ₁, СС₁ түзулері бір нүктеде қиылысу не барлығы параллел болуының қажетті және жеткілікті шарты АС₁/С₁В∙ВА₁/А₁С∙СВ₁/В₁А=1 (*) теңдігі орындалуы болып табылады.

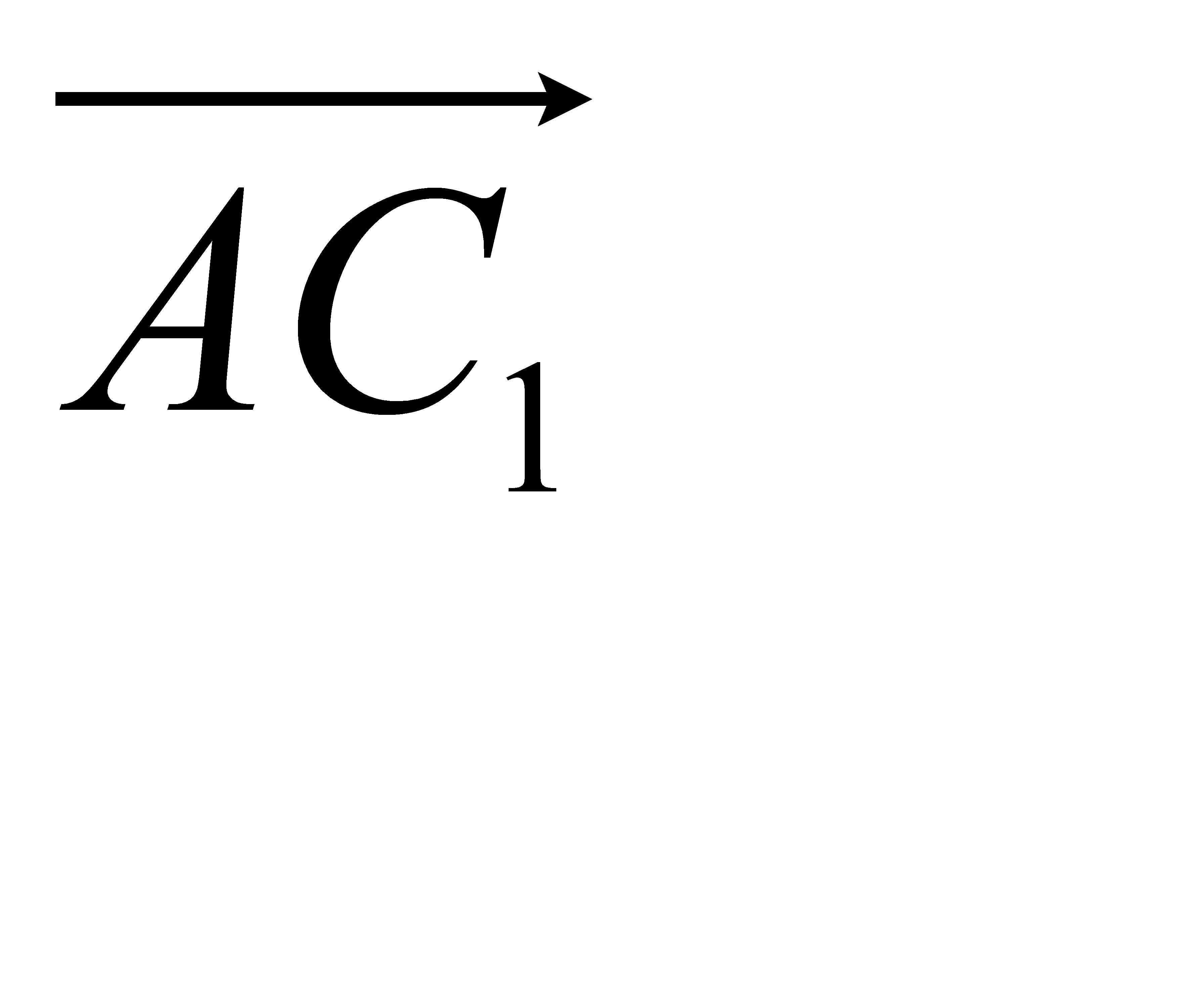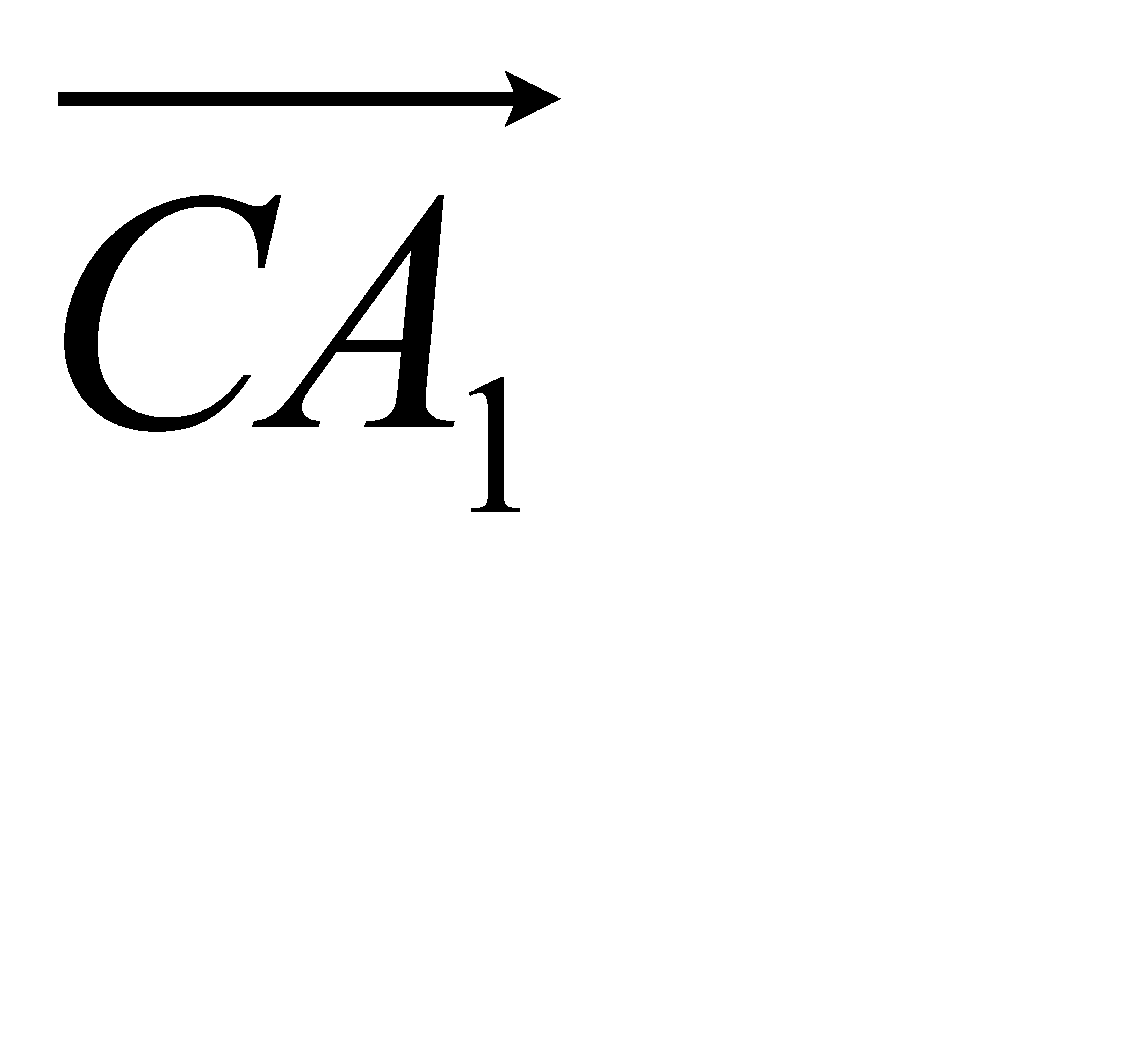Дәлелдеме: Алдымен Чевтің тура теоремасын немесе үш түзу бір нүктеде қиылысса (*) теңдік орындалатынын дәлелдейік. К нүктесі А мен А₁, В мен В₁, С мен С₁ нүктелерінің арасында жататындықтан , мен , мен , мен 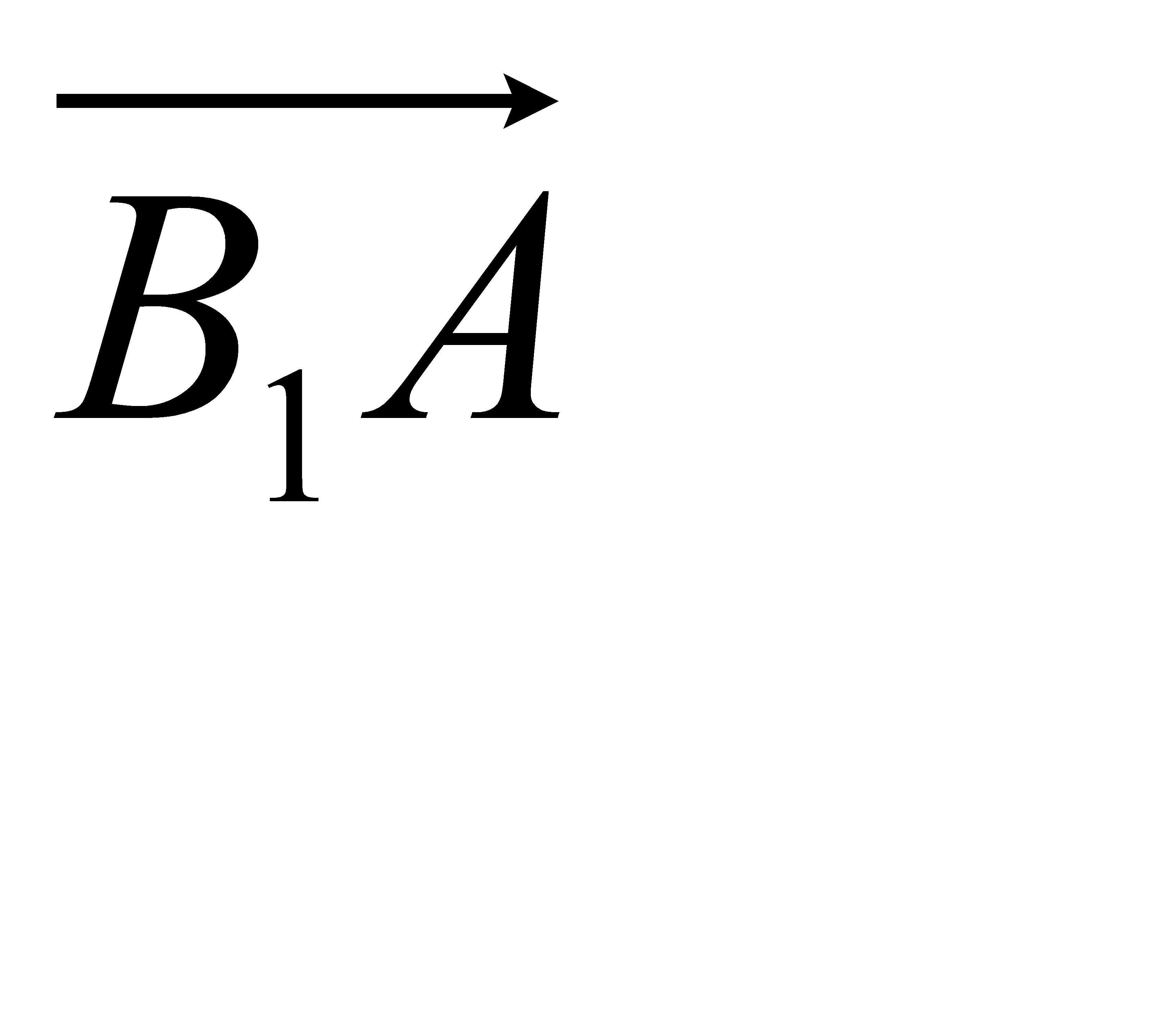векторларының бағыты бірдей. А нүктесін бастыра ВС түзуіне параллел тартылған түзумен ВВ₁, СС₁ түзулерінің қиылысу нүктелерін сәйкес N, M десек

∆МАС₁ ~ ∆СС₁В → ∆ANB₁ ~ ∆CBB₁ →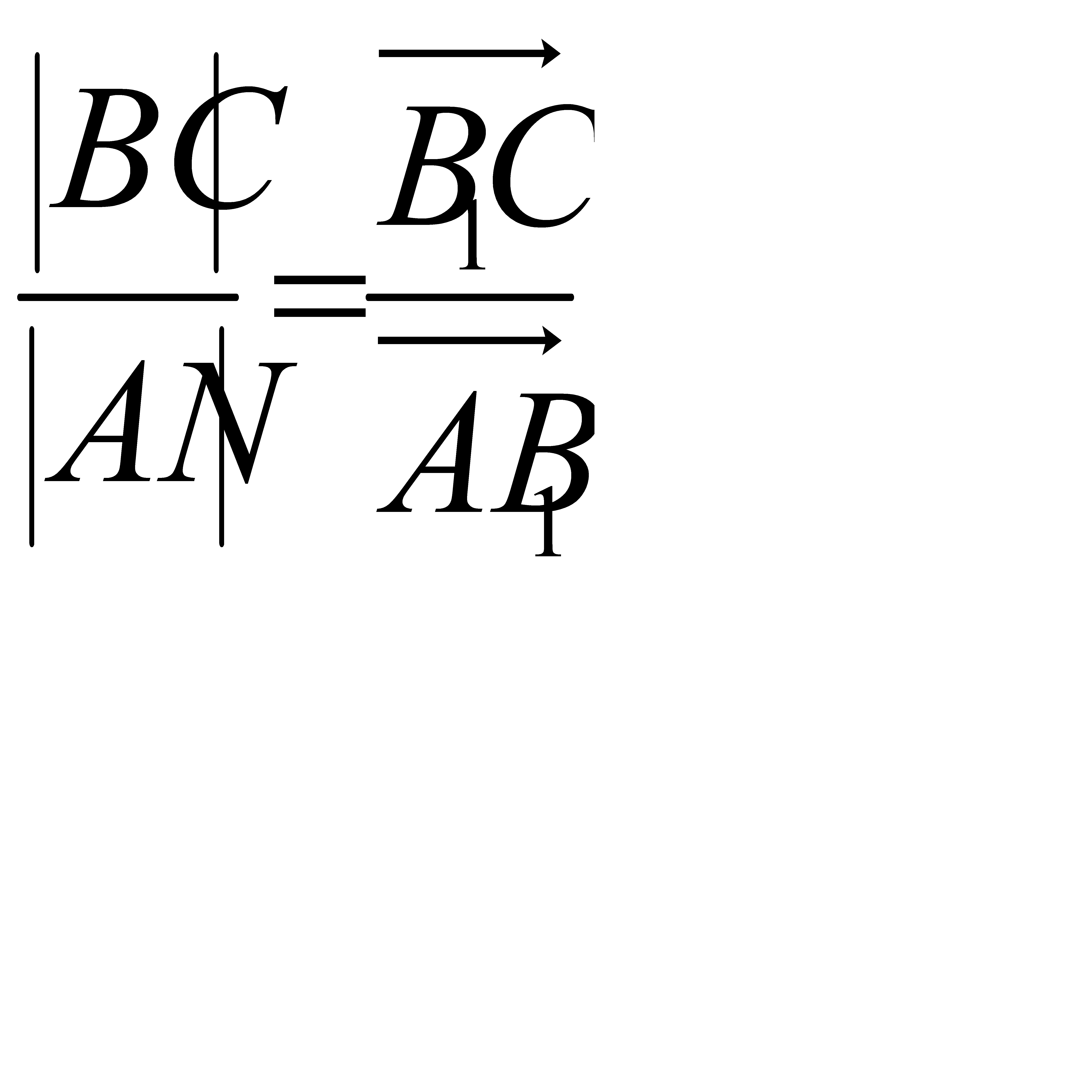

∆ANK ~ ∆A₁BK → 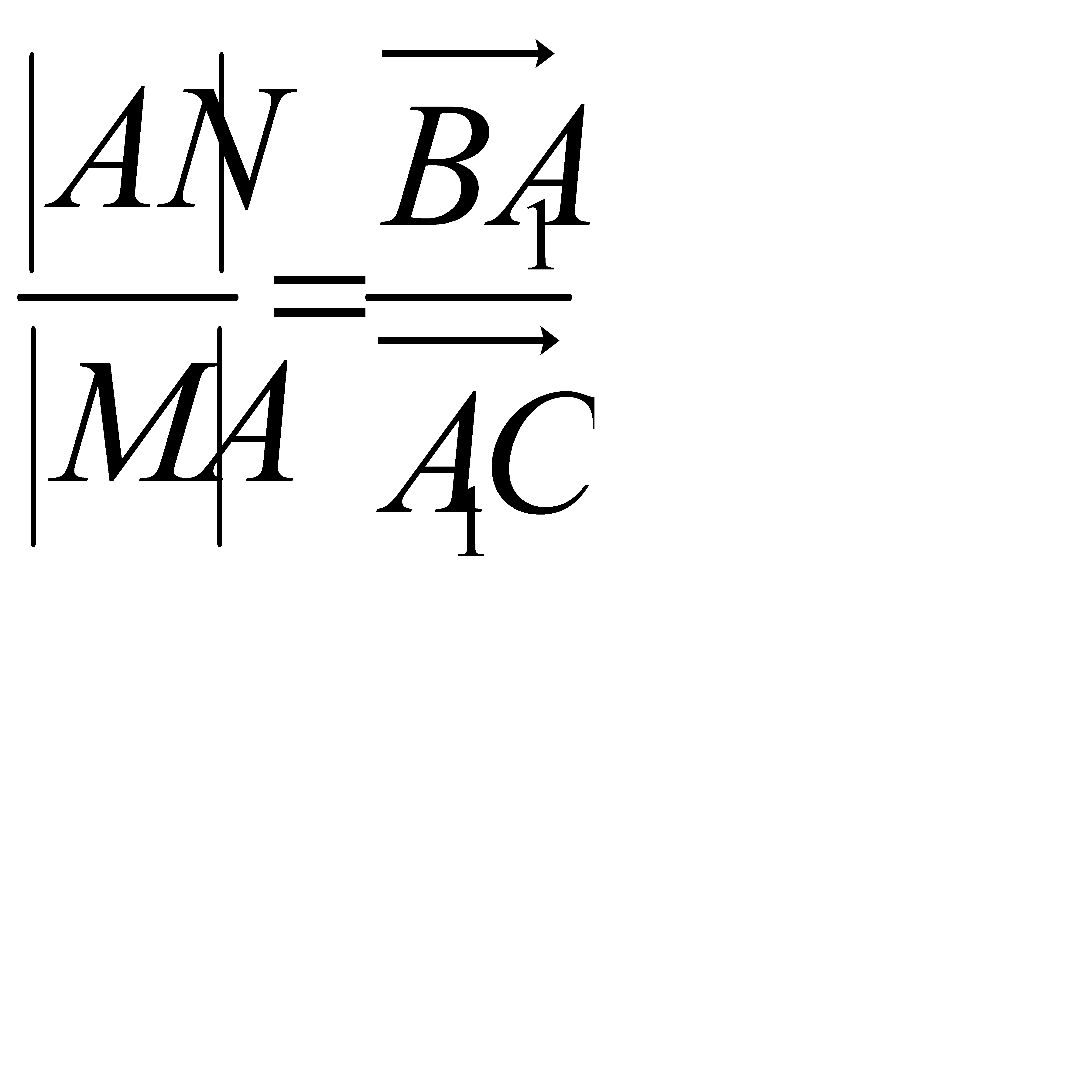және осы теңдікті мүшелеп көбейтсек:

· · ; АА₁, ВВ₁, СС₁ - лер параллел кезінде Фалес теоремасын пайдаланып оңай дәлелдейміз.

Жаттығу есептер:

5-1. Чев теоремасын пайдаланып теорема–1-ді дәлелде.

5-2. Теорем – 2 ні дәлелде.

5-3. Теорем – 3 және 6-ны Чев теоремасын пайдаланып дәлелде.

5-4. АВС үшбұрышының ішіндегі О нүктесі үшін АО, ВО, СО түзулерінің үшбұрыш қабырғаларымен қиылысатын нүктелерін сәйкесінше А₁, В₁, С₁ десек ОА₁·ОВ₁·ОС₁ көбейтіндісі ең кіші болатын О нүктесін тап.

5-5. Шеңбер АВС үшбұрышының АВ қабырғасын С₁, С₂; ВС қабырғасын А₁, А₂; СА қабырғасын В₁, В₂ нүктелерінде қиятын болсын. Егер АА₁, ВВ₁, СС₁ түзулері бір нүктеде қиылысатын болса АА₂, ВВ₂, СС₂ түзулері де бір нүктеде қиылысатынын дәлелде.

5-6. Үшбұрыш Чевиандарының табандары төбесі болатын үшбұрыштың ауданы алғашқы үшбұрыш ауданының -інен артпайтынын дәлелде.

ІІ бөлім.

Олимпиада, жарыстар ұйымдастыруға

арналған жаттығу нұсқаулары

V-VІ сынып

Бірінші нұсқа

1. 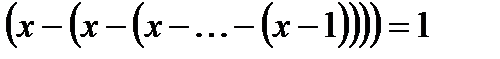(Барлығы 101 жақша) теңдеуді шеш.

2. Торда 13 алма бар. Кез келген екеуінің салмағын бір жолда өлшеуге болатын таразы бар болса 8 рет өлшеп барлық алманың салмағының қосындысын табуға бола ма?

(Бір алманы жеке өлшеу мүмкін емес)

Нұсқау: 6 ретте неше алманың салағының қосындысын таба аламыз? Соңғы өлшеген екі алманың әр қайсысымен өлшеп қалған бір алманың салмағын анықтауға болатынын пайдалан.

3. Тақтаға 20 дана 1,1 саны, 20 дана 1,11 саны жазылған. Қалған сандардың қосындысы 19,93 болатындай бірнеше санды өшірген. 1,1 және 1,11 сандарының әр қайсысынан неше сан өшірілген?

Нұсқау: теңдігі орындалатындай натурал x-пен y- тің барлық пар мәндерін тап. 19,93 саны 1,11 мен 1,1 сандарына бүтіндей бөлінбейтініне көз жеткіз.

4. Шаршыны пайда болған бөліктерден әр қабырғалы сүйір бұрышты үшбұрыш құрастыруға болатындай етіп үш бөлікке бөл.

5. Саяхатшылар тобы 11.00 сағатта тұрағынан шығып 30минут жүрген кезде біреуі компасын тұрақта қалдырғанын біліп қайта барып компасын алып 13.00 сағатта жолдастарын қуып жетті. Ол дәл неше сағатта базаға қайтып барған.

Нұсқау: Ол бұл уақытта немесе екі сағатта жолдастарының 2 сағ + 30 мин ∙ 2 = 3 сағ жүретін жолын жүрді. Ал тұраққа дейін жолды саяхатшылар тобы 30минутта жүргенін ескер.

Екінші нұсқа

1. Бірдей 24 торсықтың бесеуінде тола онбірінде тең ортасынан келетін қаймақ бар. Әр бөліктегі қаймақтың салмағы мен торсықтың саны тең болатындай етіп үш бөлікке қалай бөлуге болады?

Нұсқау: Барлық қаймақты 5 ∙ 2 + 11= 21 жарты қаймағы бар торсық деп есептесек әр бөлікте 8 торсық, 7 жарты торсыққа тең қаймақ болу керек.

2. а) А саны 5-ке бөлінеді, б) А саны 23-ке бөлінеді, в) А + 7 бүтін санның квадраты болады, г) А – 10 бүтін санның квадраты болады деген сөйлемдердің екеуі ақихат, екеуі жалған болатын барлық екі таңбалы А санын тап?

Нұсқау: а) және б) ақихат болу мүмкін емес екенін дәлелде. а) мен г), б) мен г), в) мен г) ақихат болатын жағдайларды қарастыр.

3. Үш таңбалы санның алдына 7 цифрын жазғанда шығатын 4 таңбалы саннан артына 7 цифрын жазғанда шығатын 4 таңбалы санды азайтса 882 шығады. Осы 3 таңбалы санды тап?

Жауап: 679

4. өрнегінің мәні натурал санның квадраты болатынын көрсет.

Жауап: 2010

5. Тіктөртбұрышты екі түзу арқылы 4 кішкене төртбұрышқа бөлгенде олардың үшеуінің ауданы сәйкес 1 см , 2 см 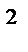, 3 см 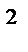болған болса үлкен төртбұрыштың ауданының ең үлкен мәні қанша болады?

Нұсқау: Бөлікте пайда болған тіктөртбұрыштардың ауданын a, b, c, d,десек ad = bc болатынына көз жеткіз.

Үшінші нұсқа

1. Алғашқы екі цифрын және ортаңғы екі цифрын өшіргенде шығатын екі таңбалы сандардың әрқайсысынан 81 есе үлкен болатын төрт таңбалы санды тап.

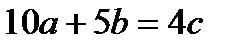Нұсқау: Есеп шартынан бұл сан түрінде болатынына көз жеткіз. шартын түрлендіріп түріне келтір.

2. 7 х 7 кестеге 1,2,3,..., 48, 49 сандарын 1-суретте көрсетілгендей орналастырған. Бұл сандардың біреуін таңдап сол сан орналасқан жол және баған бойындағы барлық сандарды өшіру амалын жалғастыра орындап кестедегі барлық сандарды өшіреді. Таңдалған сандардың қосындысын тап. Бұл қосындының мәні таңдау түріне тәуелді ме?

3. Периметрі 50 см тіктөртбұрышты 3-суретте кескінделгендей қабырғаларына параллель түзулер жүргізу арқылы тіктөртбұрыштарға бөлінеді. Жүргізілген түзулер арқылы пайда болған бөліктер болушы 9 кішкене тіктөртбұрыштардың периметрлерінің қосынындысын тап.

4. Ұзынды қысқалы 36 бөрене бар еді. Ұзындарын 6 бөлікке, қысқаларын 5 бөлікке бөліп аралады. Барлық ұзын бөліктерді аралаған саны барлық қысқа бөліктерін аралаған санына тең болса барлығы неше рет аралап кескен?

Нұсқау: Ұзын және қысқа бөліктердің қатынасы 5: 4 қатынасында болатыны анықта. Жауап: 160 рет

5. Суретте теміржол, оның бойындағы үш станциялар арқылы А және Б ауылдарына қатынасатын асфалт жолдар үздік сызықтармен кескінделген. Жолаушы А дан Б ге қарай қай жолмен жүрсе ең қысқа жол жүреді?

Нұсқау: 6-суретте кескінделген симметрияны пайдала-нып қорытынды жаса.

Төртінші нұсқа

1. Автобуста келе жатқан жолаушы жол бойымен қарама-қарсы бағытта бара жатқан досын көреді де онымен жолығу үшін 10 секундтан соң автобустан түсіп, артынан қуады. Ол досынан екі есе жылдам, автобустан бес есе жай жүрген болса досын неше секундта қуып жетеді?

Нұсқау: Автобус досынан он есе жылдам жүретіні түсінікті. Олай болса автобус тоқтағанша досы автобустың 1 секундта жүретін жолын жүрді. Немесе ол досынынң артынан қуатын кезде олардың ара-қашықтығы досының 110 секундта жүретін жолына тең.

2. Ибраһим 20 есепті тест тапсырмасын орындап орташа (1 есепке) 3,5 ұпай жинады. Неше сұрақтан ұпайын 1-мен арттырса оның орташа ұпайы 4-ке тең болады.

3. Сыныпта 30 оқушы бар. Әр оқушы дәл k оқушыны ұнатады. k-ның ең кіші қандай мәнінде сыныпта бірін-бірі ұнататын кемінде бір пар табылатын болады. Жауап:15

4. 3 х 3 кестесінің әр көзінде 0 цифр жазылған. 2 х 2 өлшемді тор көздерді таңдап алып, көздеріндегі сандардың төртеуін де 1-мен арттыру амалын қайталау арқылы төменгі кестені шығара аламыз ба?

Нұсқау:

7-ші суреттегі кестеден есеп шартындағы амалдың кері амалын орындап барлық көздердегі сандарды 0 болдыра аламыз ба?- деген есепті қарастыр. Мәселен сол жақ жоғарғы 2 х 2 тор көзді сандардан 1-ді 4 рет шегерсек 8- суреттегі нәтиже шығады. Жауап: мүмкін емес.

6. Суретте 13 нүкте кескінделген.Осы нүктелерде төбелер болтын неше шаршы сызуға болады?

Жауап: 11 шаршы.

Бесінші нұсқа

1. Қосындысы 407-ге тең 3 санның көбейтіндісі ең көп деген.де неше 0 мен аяқталады.

Нұсқау: Бұл көбейтінді 5-тің ең үлкен неше дәрежесіне бөлінуі мүмкін екенін қарастырамыз. Көбейтіндінің құрамында 5-тің дәрежесі көп болу үшін екі қосылғыш 5-тің дәрежелеріне бөлінуі қажет. Жауап: Алты 0 мен

2. Ұзындығы 30 см A B кесіндісінде A-дан B-ге қарай тізбектеліп K,L,N нүктелерін AL=MB=11см, KM=13, LN=15см болатындай етіп алған болса осы нүктелердің қатар орналасқан пар нүктелердің ара-қашықтықтарын тап.

Нұсқау: Берілген кесінділердің ұзындықтарын қосқанда AK,MB кесінділерінің ұзындығы бір бір рет KL,LM, MN кесінділерінің ұзындықтары екі екі рет кіреді. Сондықтан KN=AL+KM+LM+MB – AB болатынына көз жеткіз.

3. x натурал саны үшін 2x > 70, x < 100, 3x > 25, x ≥ 10, x > 5 теңсіздіктерінің екеуі жалған үшеуі ақихат болса х-тің мәнін анықта.

Дата добавления: 2014-12-16