По математике 2012 года

Класс, 1 день

Класс, 2 день

Класс, 1 день

Класс, 2 день

Класс, 1 день

Класс, 2 день

Класс, 1- день

1. Числа a, b, c таковы, что 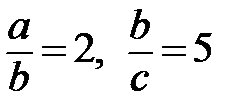. Найдите значение выражения .

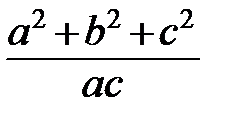2. Учитель физкультуры хочет выстроить в шеренгу (линию) 60 школьников – 29 мальчиков и 31 девочку так, чтобы ни один из школьников (девочка или мальчик) не стоял между двумя девочками. Удастся ли ему это?

3. A, B, C – три различные нечетные цифры. Известно, что 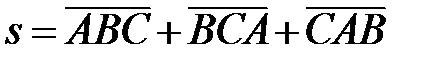– трехзначное число. Найдите s. Через 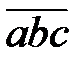обозначается число, десятичная запись которого состоит из цифр a, b, c в указанном порядке.

Жиырма алтыншы нұсқа

2011 жылғы оқушылардың Республикалық математикалық олимпиадасының II кезеңі

8 класс, 2-ші күн

4. Теңдеуді шешіңдер: .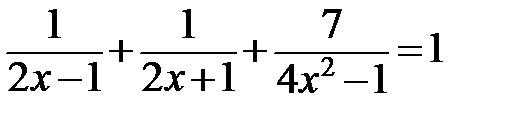

5. 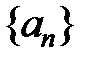сандар тізбегі былай анықталған: 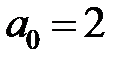және әрбір 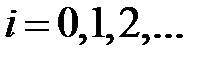үшін 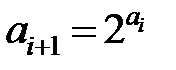. Кейбір теріс емес, бүтін 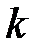саны үшін 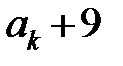түрінде өрнектелетін жай сандардың бәрін табыңдар. Нұсқау: 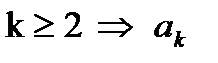сандары 6-мен аяқталатынын анықтап, сондықтан да 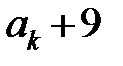-дың алғашқы екі мәні ғана жай сан болатынын дәлелде.

6. ABCD квадратының сыртынан 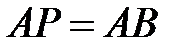және 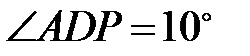болатындай етіп P нүктесі алынған. 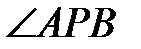бұрышының мүмкін (градустық) мәндерін анықтаңдар.

4. Решить уравнение: .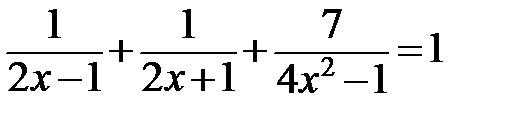

5. Последовательность 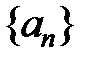определяется следующим образом: 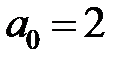и 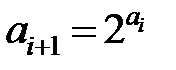для каждого 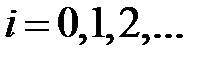. Найдите все простые числа, представимые в виде 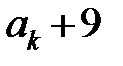для некоторого неотрицательного, целого .

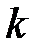6. Вне квадрата ABCD взяли такую точку P, что 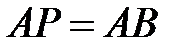и 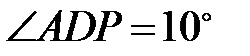. Найдите возможные значения (в градусах) величины угла .

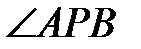Жиырма алтыншы нұсқа

2011 жылғы оқушылардың Республикалық математикалық олимпиадасының II кезеңі

9 класс, 1-ші күн

1. Денешынықтыру мұғалімі 60 оқушыны – 29 ұл бала мен 31 қыз баланы – бір шеренганың (түзудің) бойына, ешбір (ұл немесе қыз) бала екі қыз баланың арасында қалмайтындай етіп, сапқа тұрғызғысы келеді. Оның бұл ойы іске аса ма?

2. Кез келген нақты 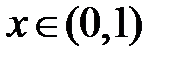саны үшін 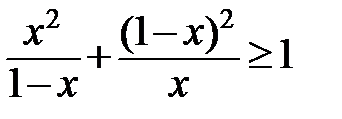теңсіздігі орындалатынын дәлелдеңдер.

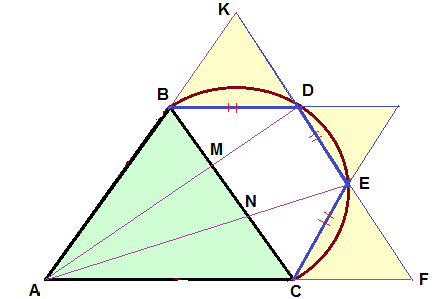
3. Теңқабырғалы ABC үшбұрышының BC қабырғасына үшбұрыштың сыртына қарай жартышеңбер тұрғызылған. Жартышеңберден BD = DE = EC болатындай етіп, D және E нүктелері алынған. AD және AE кесінділері BC қабырғасын тең үш бөлікке бөлетінін дәлелдеңдер. Нұсқау: Төменгі суреттен KD = BD = DE = EА =EС теңдігіне және KF//BC болатынына көз жеткізіп, ұқсастықты пайдалана отырып BM = MN = NC теңдігін дәлелде.

4. Учитель физкультуры хочет выстроить в шеренгу (линию) 60 школьников – 29 мальчиков и 31 девочку так, чтобы ни один из школьников (девочка или мальчик) не стоял между двумя девочками. Удастся ли ему это?

5. Докажите, что для любого вещественного 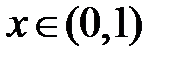выполняется неравенство .

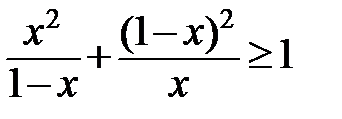6. На стороне BC равностороннего треугольника ABC построена полуокружность, лежащая вне треугольника. На ней выбраны точки D и E так, что BD = DE = EC. Докажите, что отрезки AD и AE делят сторону BC на три равные части.

Жиырма жетінші нұсқа

2011 жылғы оқушылардың Республикалық математикалық олимпиадасының II кезеңі

9 класс, 2-ші күн

4. 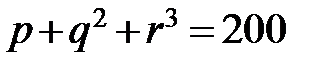теңдеуін қанағаттандыратын барлық p, q, r жай сандар үштіктерін табыңдар (немесе табылмайтынын дәлелдеңдер).

5. ABCD квадратының сыртынан 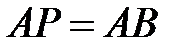және 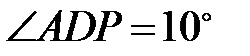болатындай етіп P нүктесі алынған. 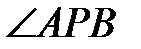бұрышының мүмкін (градустық) мәндерін анықтаңдар.

6. Жазықтықта барлық өзара ара қашықтықтары натурал сандарға тең болатын, бір түзудің бойында жатпайтын әртүрлі 2011 нүкте табылатынын дәлелдеңдер. Нұсқау: Тік бұрышты координаталар жүиесінде есеп шартын қанағатандыратын нүктелерді координата остерінің бойында іздестірейік. Ордината осінің бойында координаталар басы және оған қарағанда симметриялы орналасатын В(0;a), С(0;-a) нүкелері алынсын.

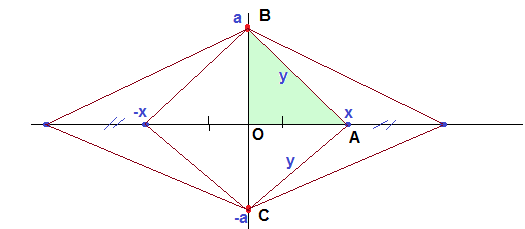
Онда біздің есебіміз 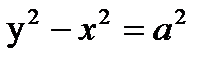Диофант теңдеуінің 1004 шешімі болатындай а параметрдің шешімін табу есебіне келіп тіреледі. Теңдеуді 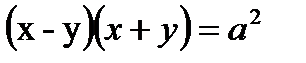түріне келтіріп 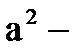ті 1004-тен кем емес бөлгіші болатындай етіп таңдасақ жеткілікті.

4. Найдите все тройки простых чисел p, q, r (или докажите, что таких нет), удовлетворяющие уравнению 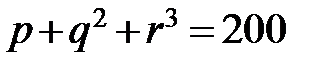. 5. Вне квадрата ABCD взяли такую точку P, что 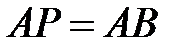и 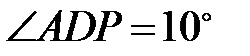. Найдите возможные значения (в градусах) величины угла .

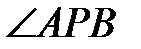6. Докажите, что на плоскости существует 2011 различных точек, не лежащие все на одной прямой, все попарные расстояния между которыми – натуральные числа.

Жиырма сегізінші нұсқа

2012 жылғы оқушылардың Республикалық математикалық олимпиадасының II кезеңі

8 класс, 1-ші күн

1. Квадраттың бір қабырғасы p %-ға ұзартылып, ал екінші қабырғасы p %-ға қысқартылды. Пайда болған тіктөртбұрыштың ауданы квадраттың ауданының 99%-ына тең болса, p -ны табыңдар.

2. Өрнекті ықшамадаңдар: .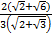

3. Теңдеуді шешіңдер: .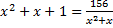

1. Одна сторона квадрата увеличена на p %, а другая уменьшена на p %. Площадь полученного прямоугольника составляет 99% от площади квадрата. Найдите p.

2. Упростите выражение: .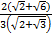

3. Решите уравнение: .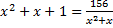

Жиырма тоғызынщы нұсқа

2012 жылғы оқушылардың Республикалық математикалық олимпиадасының II кезеңі

8 класс, 2-ші күн

4. Оң бүтін a, b, c сандары

abc + ab + bc + ac + a + b + c =1000

тепе-теңдігін қанағаттандыратын болса, a + b + c қосындысын табыңдар. Нұсқау: Қосынды тұрақты болған кезде қосылғыштар бір біріне жақындаған сайын олардың көбейтіндісі өсіп қосылғыштар теңескенде өзінің ең үлкен мәнін қабылдайды. Мәселен a + b + c=27 деп көрсек 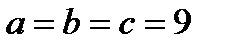болған кезде abc + ab + bc + ac + a + b + c =999 ең үлкен мән бола-тындықтан қосындының мәні 27-ден үлкен болу керек. Сондай-ақ берілген қосынды a; b; c үшеуі де жұп болған кезде ғана жұп мәнге ие болады. Сондықтан ізделінді мән a + b + c = 28 болуы мүмкін. Мүмкіндіктерді тексере отырып a =12; b =10; c = 6 кезде abc + ab + bc + ac + a + + b + c =1000 болатынына көз жеткіз. Басқа мән табыла ма дегенге қорытынды жаса.

5. A, B, C, D, E жануарларының әрқайсысы немесе қасқыр, немесе ит екені белгілі. Иттер әрқашан шын, ал қасқырлар әрқашан өтірік сөйлейді. A: «B – ит», – деді. C: «D – қасқыр», – деді. E: «A – ит», – деді. B: «C – қасқыр», – деді. D: «B мен E – әр түрлі жануарлар», – деді. A, B, C, D, E жануарларының арасында қанша қасқыр бар екенін анықтаңдар. Нұсқау: А ит, А қасқыр болатын екі мүмкін жағдайды қарастырып қорытынды жасау керек.

6. N жұмысшы N тонна өнім шығару үшін N күн бойы N сағаттан жұмыс істеуі тиіс. M жұмысшы M күн бойы M сағаттан жұмыс істесе, қанша тонна өнім шығарады? Нұсқау: Бір жұмысшы бір күнде бір сағат жұмыс істеп қанша тонна өнім шығаратынын есепте.

4. Целые положительные числа a, b, c удовлетворяют соотношению:

abc + ab + bc + ac + a + b + c =1000.

Найдите сумму a + b + c.

5. Каждое из пяти животных A, B, C, D, E – либо волк, либо собака. Собаки всегда говорят правду, а волки всегда врут. A утверждает, что B – собака. C утверждает, что D – волк. E утверждает, что A – собака. B утверждает, что C – волк. D утверждает, что B и E – животные разных видов. Найдите количество волков среди животных A, B, C, D, E.

6. N рабочих производят N тонн продукта, работая N дней по N часов. Сколько тонн продукта произведут M рабочих, работая M дней по M часов?

Отызыншы нұсқа

2012 жылғы оқушылардың Республикалық математикалық олимпиадасының II кезеңі

9 класс, 1-ші күн

1. 10-нан аспайтын натурал m және n сандарының көмегімен түрінде қанша әртүрлі сан жасай аламыз? Мысалы, 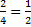болатынын ұмытпаң-дар.

4. Әр түзу дәл төрт басқа түзумен қиылысатындай етіп, жазықтықта, ең көп дегенде, қанша түзу жүргізе аламыз?

5. 4⁵⁰·5¹⁰⁵ санының ондық жазбасында қанша цифр бар? Нұсқау: Берілген өрнекті 10¹⁰⁰·5⁵ түріне келтір.

1. Сколько различных чисел можно записать в виде , где m и n – натуральные числа, не превосходящие 10? Заметьте, что, например, .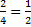

4. Какое наибольшее количество прямых можно провести на плоскости так, чтобы каждая прямая пересекала ровно четыре другие?

5. Сколько цифр содержит десятичная запись числа 4⁵⁰·5¹⁰⁵?

Отыз бірінші нұсқа

2012 жылғы оқушылардың Республикалық математикалық олимпиадасының II кезеңі

9 класс, 2-ші күн

4. Би үйірмесіне 6 ұл бала және 6 қыз бала қатысады. Оларды қанша әдіспен ұл-қыз парларына бөлуге болады? Нұсқау: 6 ұлды орындық деп есептеп 6 орындыққа 6 қызды неше әр түрлі тәсілмен отырғызуға болатынын есепте.

5. Қаржы министрі мемлекетте айналысқа тек қана 33 және 60 ақша бірлігіне тең монеталар түсетінін бекітті. Егер олардың әрқайсысында монеталардың әр түрі жеткілікті мөлшерде болса, сатып алушы сатушыға қандай ең аз оң соманы төлей алады? Нұсқау: 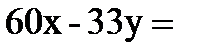a теңдеуінің бүтін шешімі болатын ең кіші натурал санды тап. Сызықтық Диофант теңдеудің бүтін шешімі болуының қажетті шартын ескер.

6. Клубтың жиырма мүшесі бар. Жаңа жылда олардың әрқайсысы клубтың 10 мүшесіне ашық құттықтау хатын жолдағаны белгілі болса, бір-біріне ашық құттықтау хатын жолдаған екі адам табылатынын дәлелдеңдер. Нұсқау: Кері жорып алсақ жолданған хаттар саны 1+2+...+19 = 190 болып 200-ге жетпейтінін түсіндір.

II этап Республиканской олимпиады школьников

Дата добавления: 2014-12-16