Несвободное твердое тело. Основные виды связей и их реакции

Твердое тело, на перемещение которого не наложено никаких ограничений, называется свободным твердым телом.

Тело, ограничивающее свободу движения данного твердого тела, является по отношению к нему связью.

Твердое тело, свобода движения которого ограничена связями, называется несвободным.

Все силы, действующие на несвободное твердое тело, наряду с делением на внешние и внутренние можно также разделить на задаваемые или активные силы и реакции связей.

Задаваемые силы выражают действие на твердое тело других тел, вызывающих или способных вызвать изменение его кинематического состояния.

Реакцией связи называется сила или система сил, выражающая механическое действие связи на тело.

Одним из основных положений механики является принцип освобождаемости твердых тел от связей,согласно которому несвободное твердое тело можно рассматривать как свободное, на которое, кроме задаваемых сил, действуют реакции связей.

Пусть на идеально гладкой неподвижной горизонтальной плоскости покоится шар (рис. 7,а). Плоскость, ограничивая движение шара, является для него связью.

Рис. 8 Рис. 7

Если мысленно освободить шар от связи (рис. 7, б), то для удержания его в покое к нему в точке касания с плоскостью нужно приложить силу 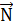, равную силе тяжести шара 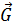по модулю и противоположную ей по направлению. Cила 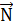и будет нормальной реакцией плоскости. Тогда шар, освобожденный от связи, будет свободным телом, на которое действуют задаваемая сила 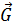и реакция плоскости .

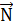Гладкая плоскость не противодействует перемещению тела вдоль плоскости под действием задаваемых сил (рис. 8, а), но не допускает его перемещения в направлении, перпендикулярном плоскости. Поэтому действие плоскости на тело выражается нормальной реакцией 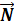(рис. 7, б).

Реакция гладкой плоскости направлена перпендикулярно плоскости.

Если к концу В нити АВ, прикрепленной в точке А, подвесить груз весом (рис. 9, а) то реакция нити будет приложена к грузу в точке В, равна по модулю его весу и направлена вертикально вверх (рис. 9, б). Реакция нити направлена вдоль нити.

Пусть балка весом G в точке В опирается на гладкую поверхность, а в точках А и D- на гладкие горизонтальную и вертикальную плоскости (рис. 10). Тогда реакции опорной поверхности и опорных плоскостей будут иметь указанные на (рис. 10) направления.

Для определения каждой реакции нужно знать три ее элемента: модуль, направление и точку приложения. Точка приложения реакции, как правило, бывает известна. Направление же реакций известно лишь для некоторых типов связей.

Если существуют два взаимно перпендикулярных направления на плоскости, в одном из которых связь препятствует перемещению тела, а в другом — нет, то направление ее реакции противоположно первому направлению.

Так, например, гладкая горизонтальная плоскость препятствует перемещению шара вертикально вниз и не препятствует его горизонтальному перемещению. В этом случае реакция плоскости направлена вверх (см. рис. 7,6). Так же определяется направление реакции нити (см. рис. 9).

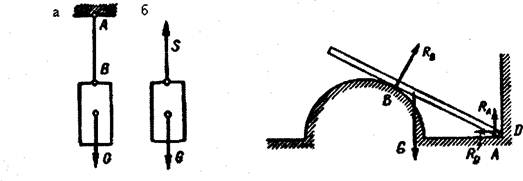
Рис. 9 Рис. 10

Гладкая поверхность, на которую опирается балка точкой В (рис. 10), препятствует перемещению балки по нормали к поверхности вниз и не препятствует перемещению вдоль оси балки. Поэтому реакция этой поверхности направлена по нормали к поверхности вверх.

Аналогично, если балка опирается на ребро в точке D (точечная опора), то реакция в, точке D направлена перпендикулярно оси балки (рис. 11).

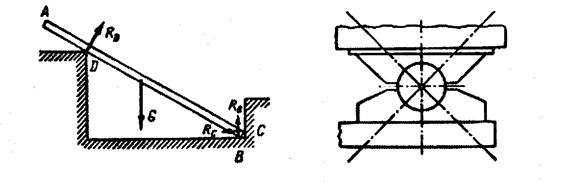
Рис. 11 Рис. 12

Рассмотрим два основных типа опор балок и их реакции.

На (рис. 12) изображена шарнирно-неподвижная опора, которая препятствует любому поступательному движению балки, но дает ей возможность свободно поворачиваться вокруг оси шарнира. По своей конструкции такая шарнирная опора состоит из двух обойм, из которых одна закреплена на балке, а другая - на неподвижной поверхности. Эти обоймы соединяются с помощью цилиндрического валика на (рис. 12) показано среднее сечение конструкции.

В зависимости от действующих сил валик может прижиматься к различным точкам обоймы. Реакция 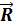шарнирно-неподвижной опоры проходит через центр шарнира О и точку соприкосновения А (рис. 13, а, б), но ее модуль и направление не известны.

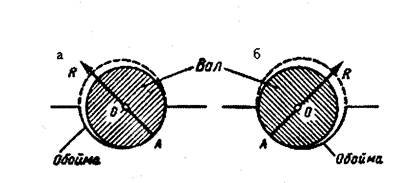
Рис. 13

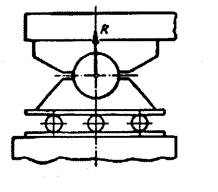
Рис. 14

Шарнирно-подвижная опора, нижняя обойма которой поставлена на катки, не препятствует перемещению балки параллельно опорной плоскости (рис. 14). Если не учитывать трения катков, то линию действия реакции такой опоры следует считать проходящей через центр шарнира перпендикулярно опорной плоскости. Таким образом, не известен лишь модуль этой реакции.

Шаровой шарнир (рис. 15) представляет собой шар, который может вращаться как угодно внутри сферической полости. Центр шара остается неподвижной точкой, через которую проходит линия действия реакции .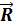

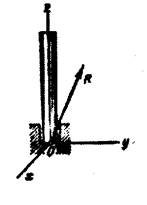
Рис. 15 Рис. 16

Подпятник (рис. 16) представляет собой совокупность цилиндрического шарнира, рассмотренного на (рис. 12) и (рис. 13), и упорной плоскости. Подпятник закрепляет одну из точек твердого тела так, что она не может совершать никаких перемещений в пространстве. Линия действия реакции 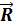подпятника проходит через эту точку.

Модули реакций шарового шарнира и подпятника и их направления в пространстве не известны. Поэтому при решении задач их раскладывают на составляющие вдоль оси координат.

Определение модулей и направлений реакций различных связей - основное содержание задач статики и излагается в курсе ниже.

В курсе теоретической механики обычно рассматривают только действие внешних сил на абсолютно твердое тело. Однако при расчете различных конструкций иногда необходимо определять внутренние силы, возникающие в растянутых и сжатых стержнях. Для определения внутренних усилий в стержнях воспользуемся так называемым методом сечений, дающим возможность принимать внутренние силы за внешние. Рассмотрим сущность этого метода.

Пусть стержень АВ, весом которого пренебрегаем, растягивается двумя равными по модулю силами 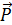₁, ₂, приложенными к его концам (рис. 1.17). Рассечем мысленно стержень, разделив его на две произвольные части AD и DB. На часть AD действуют две уравновешивающиеся силы: внешняя сила ₁ и внутреннее усилие , заменяющее действие отброшенной части стержня. Из второй аксиомы следует, что внутреннее усилие ₁ направлено по оси стержня и равно по модулю силе 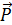₁. Внутреннее усилие ₁, выражающее действие отброшенной части DB на рассматриваемую AD, является по отношению к рассматриваемой части стержня внешней силой. Аналогично на часть DB, кроме силы ₂, действует внутреннее усилие ₂, заменяющее действие части AD.

Рис. 17 Рис. 18

Если стержень АВ растягивается (рис. 18, а) или сжимается (рис. 18, б) силам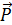и ₁ и ₂, то на тела, вызывающие его растяжение или сжатие, со стороны стержня действуют реакци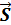и ₁ и 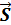₂. При этом реакции растянутого стержня равны по модулю задаваемым силам и направлены по оси стержня от его концов внутрь стержня.

Реакции сжатого стержня равны по модулю задаваемым силам и направлены по оси стержня к его концам. Так как реакции и внутренние усилия по модулю равны, то для определения усилия в стержне достаточно определить его реакцию.

7. Аксиома об освобождаемости от связей.Не изменяя движения или равновесия твердого тела, можно отбросить наложенные на нее связи, заменяя их действие реакциями отображенных связей.

Дата добавления: 2014-12-16