
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проекции силы на оси декартовых координат
|
|
|
|
Взяв правую систему неподвижных осей декартовых координат х, у и z, разложим силу 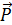 по правилу параллелепипеда на три составляющие силы
по правилу параллелепипеда на три составляющие силы  x
x  v и
v и  г, направленные параллельно этим осям (рис. 27).
г, направленные параллельно этим осям (рис. 27).
Силы  x
x  v и
v и  г, называются компонентами силы по осям х, у и z.
г, называются компонентами силы по осям х, у и z.
Алгебраические значения длин направленных отрезков Аа, АЬ и Аc называются проекциями силы на оси х, у и z.
Обозначив 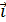 ,
, 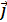 и
и  единичные векторы, направленные по осям x, у и z, а X, Y и Z-
единичные векторы, направленные по осям x, у и z, а X, Y и Z-
проекции силы на эти оси, получим  =
=  x +
x +  v +
v +  г
г
Но
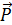 x =
x = 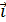 X;
X; 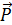 у =
у = 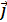 Y;
Y; 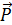 z =
z = 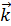 Z;
Z;
поэтому
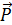 =
= 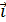 X +
X + 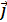 Y +
Y + 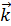 Z(1.2)
Z(1.2)
Равенство (1.2) представляет собой формулу разложения силы на составляющие по осям координат.
Проекция силы на каждую координатную ось определяется произведением модуля силы на косинус угла между направлениями оси и силы:
X = Pcos(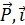 ); Y = Pcos(
); Y = Pcos(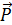 ,
, 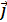 ); Z = Pcos(
); Z = Pcos(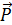 ,
, 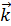 ),(1.3)
),(1.3)
где (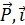 ), (
), (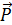 ,
, 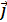 ), (
), ( ,
,  ) - углы, заключенные между направлением силы
) - углы, заключенные между направлением силы  и направлениями осей x,y и z.
и направлениями осей x,y и z.
Если известны проекции силы на три взаимно перпендикулярные оси х, у и z, то модуль и направление силы определяются по следующим формулам:
P= 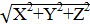 ;
;
cos(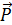 ,
, 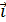 ) =
) =  ; cos(
; cos(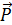 ,
, 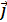 ) =
) =  ; cos(
; cos(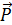 ,
, 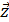 ) =
) =  .
.
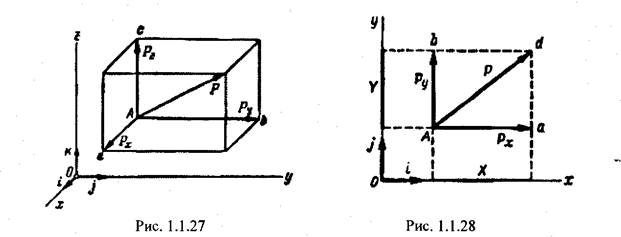
Если рассматриваются силы, лежащие в одной плоскости, то, взяв две взаимно перпендикулярные оси х и у в этой плоскости, каждую силу 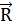 можно разложит составляющие силы
можно разложит составляющие силы  к и
к и  у, направленные параллельно этим осям (рис. 28).
у, направленные параллельно этим осям (рис. 28).
В этом случае
 =
=  x+
x+  у или
у или  =
= 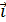 X+
X+ 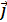 Y.
Y.

Модуль и направление силы определяются по проекциям:
В формуле (1.3) X = P cos( ,
, 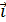 ) угол (
) угол ( ,
, 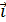 ), как известно, представляет собой угол α между направлениями силы Р и оси х, проведенной через точку приложения силы (рис. 29). Этот угол отсчитывается от оси по часовой стрелке или против; он не должен превышать 180° при любом направлении силы.
), как известно, представляет собой угол α между направлениями силы Р и оси х, проведенной через точку приложения силы (рис. 29). Этот угол отсчитывается от оси по часовой стрелке или против; он не должен превышать 180° при любом направлении силы.
При вычислении проекции силы на ось возможны следующие частные случаи:
1. Проекция положительна:
∠ α< 90°; X= P cos α.
2. Проекция равна нулю:
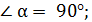 X = P cos 90° = 0.
X = P cos 90° = 0.
3. Проекция отрицательна:
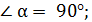 X = P cos α = - P cos β,
X = P cos α = - P cos β,
где β - острый угол между линией действия силы и осью.
При решении задач рекомендуется вычислять абсолютное значение проекции силы как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции непосредственно по чертежу.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 3334; Нарушение авторских прав?; Мы поможем в написании вашей работы!