Сложение пар сил. Условие равновесия пар сил

Теорема об условии эквивалентности пар сил в пространстве.

Вместо вектора момента каждой пары сил, перпендикулярного плоскости чертежа, указывают только направление, в котором пара сил стремится вращать эту плоскость.

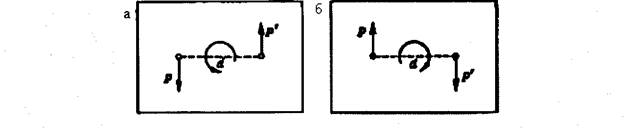
Рис. 33

Пары сил в пространстве эквивалентны, если их моменты геометрически равны.

Не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости действия пары, а также изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента.

Таким образом, вектор момента пары сил можно переносить в любую точку, т. е. момент пары сил является свободным вектором.

Вектор момента пары сил определяет все три ее элемента: положение плоскости действия пары, направление вращения и числовое значение момента.

Рассмотрим сложение двух пар сил, расположенных в пересекающихся плоскостях, и докажем следующую теорему: геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары.

Пусть требуется сложить две пары сил, расположенные в пересекающихся плоскостях I и II имеющие моменты ₁ и ₂ (рис. 34).

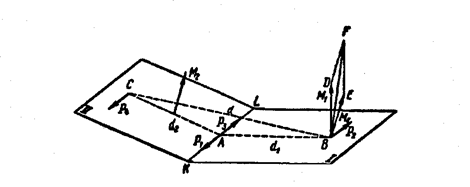
Рис. 34

Выбрав силы этих пар равными по модулю Р₁ = Р₂ = Р₃ = Р₄ = Р, определим плечи этих пар:

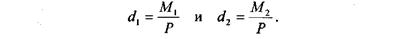
Расположим эти пары сил таким образом, чтобы силы ₁ и ₃ были направлены по линии пересечения плоскостей KL в противоположные стороны и уравновешивались. Оставшиеся силы ₂ и ₄ образуют пару сил, эквивалентную данным двум парам сил. Эта пара сил имеет плечо ВС = d и момент, перпендикулярный плоскости действия пары сил, равный по модулю М= Pd.

Геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной пары. Так как момент пары сил является свободным вектором, перенесем моменты составляющих пар сил ₁ и ₂ в точку В и сложим их, построив на этих моментах параллелограмм.

Диагональ этого параллелограмма 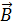F= ₁+ ₂ представляет собой момент

эквивалентной пары ₂, ₄. Отсюда следует, что вектор F= , т. е. геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары сил:

₁+ ₂= .

Такой способ сложения моментов пар сил называется правилом параллелограмма моментов. Построение параллелограмма моментов можно заменить построением треугольника моментов.

Применяя построение параллелограмма или треугольника моментов, можно решить и обратную задачу, т. е. разложить любую пару сил на две составляющие.

Пусть требуется сложить несколько пар сил, расположенных произвольно в пространстве (рис. 35). Определив моменты этих пар, их можно перенести в любую точку О пространства. Складывая последовательно моменты этих пар сил, можно построить многоугольник моментов пар, замыкающая сторона которого определит момент эквивалентной им пары сил.

На (рис. 35) показано построение многоугольника моментов при сложении трех пар.

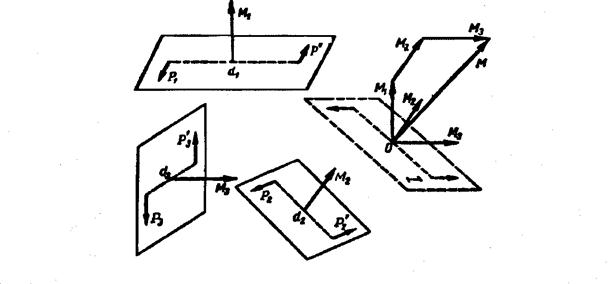
Рис. 35

Момент пары сил, сил, эквивалентной данной системе пар сил в пространстве, равен геометрической сумме моментов составляющих пар сил:

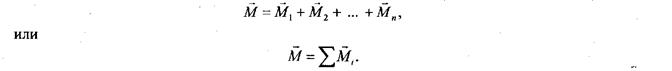
Плоскость I действия этой пары сил перпендикулярна направлению ее момента . Если момент эквивалентной пары сил равен нулю, то пары сил взаимно уравновешиваются:

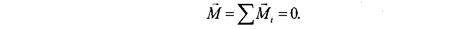
Таким образом, условие равновесия пар сил, произвольно расположенных в пространстве, можно сформулировать так: пары сил, произвольно расположенные в пространстве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю.

Если пары сил расположены в одной плоскости (рис. 36), то моменты этих пар сил, направленные по одной прямой, складываются алгебраически.

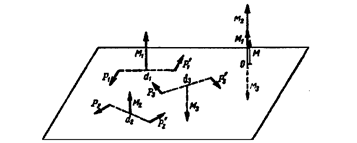
Рис. 36

Дата добавления: 2014-12-16