Приведение силы к заданному центру

Тема 4. Произвольная плоская система сил.

Цели и задачи изучения темы:

Результат освоения темы:

Индекс компетенции	Индекс образовательного результата	Образовательный результат

Пусть даны сила Р, приложенная к твердому телу в точке А, и произвольная точка О, которую назовем центром приведения. Проведем из точки О в точку А радиус-вектор r (рис. 53, а) и определим момент силы Р относительно центра приведения:

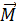₀= ×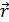

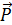
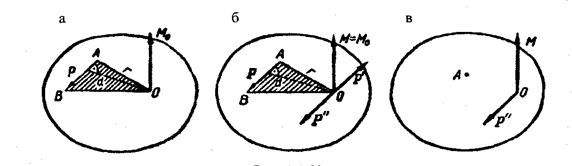
Рис. 53

Приложим в точке О две уравновешивающиеся силы ' и ", равные и параллельные силе 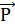(рис. 53,6). Получим эквивалентную силе систему трех сил , ’ и ", которую можно рассматривать как совокупность силы "( "= ), приложенной в центре приведения О и присоединенной пары сил , '.

Опустив из точки О перпендикуляр на линию действия силы , получим плечо этой пары сил и найдем модуль ее момента

равный модулю момента силы относительно центра приведения О.

Вектор М момента присоединенной пары сил направлен перпендикулярно плоскости пары , ’, совпадающей с плоскостью треугольника ОАВ, в ту сторону, с которой пара , ’ представляется стремящейся вращать эту плоскость в сторону, противоположную вращению часовой стрелки. Приложив его как свободный вектор в центре приведения О, убедимся, что направление совпадает с направлением вектора ₀ момента силы относительно центра приведения.

Так как эти векторы равны по модулю и совпадают по направлению, то они геометрически равны, т. е.

Таким образом, силу , не изменяя ее действия на твердое тело, можно перенести из точки ее приложения А в любой центр приведения О, приложив при этом к телу пару сил с моментом , геометрически равным моменту ₀ этой силы относительно центра приведения(рис. 53,в).

Этот метод был предложен французским ученым Пуансо (1777 - 1859) и называется приведением силы к заданному центру.

Дата добавления: 2014-12-16