Уравнения равновесия системы сил, произвольно расположенных на плоскости

Для сил, произвольно расположенных на плоскости, имеются два условия равновесия:

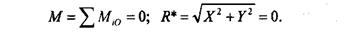
Из второго условия следует, что X = Ʃ X ₁= 0 и Y = ƩY₁= 0. Таким образом, два условия равновесия сил, произвольно расположенных на плоскости, можно выразить в виде системы трех уравнений:

Ʃ M _iO=0; Ʃ X _i=0; Ʃ Y _i=0.

Эти уравнения называются основными уравнениями равновесия плоской системы сил(универсальная форма). Центр моментов и направление координатных осей для этой системы уравнений можно выбрать произвольно.

Существует и две другие системы трех уравнений равновесия сил – системы:

Ʃ M _iA=0; Ʃ M _iB=0; Ʃ U _i=0, (1.6)

при этом ось U не должна быть перпендикулярна прямой проходящей через точки А и В;

Ʃ M _iA=0; Ʃ M _iB=0; Ʃ U _iС=0, (1.7)

точки А, В, и С не должны лежать на одной прямой.

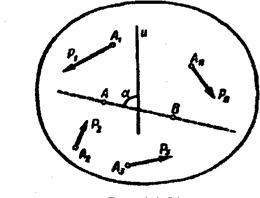
Рис. 55

Пусть дана система сил, произвольно расположенных на плоскости

₁, ₂,..., _п (рис. 55), удовлетворяющая трем уравнениям равновесия (1.6):

Ʃ M _iA=0; Ʃ M _iB=0; Ʃ U _i=0;

причем ось U не перпендикулярна прямой АВ.

Известно, что неуравновешивающиеся силы, произвольно расположенные на плоскости, приводятся или к паре сил, или к равнодействующей.

Так как главные моменты системы сил относительно двух центров равны нулю, то рассматриваемая система сил не приводится к паре сил. При наличии пары сил главные моменты системы сил относительно всех точек плоскости одинаковы и равны моменту этой пары (см. теорему о моменте пары сил).

Если силы приводятся к равнодействующей силе, то ее линия действия должна проходить через точки А и В, так как на основании теоремы Вариньона

M_A ( )= Ʃ M _iA=0; M_B ( )= Ʃ M _iB=0;

Но проекция равнодействующей на любую ось равна сумме проекций составляющих сил, т. е.

R cos α = Ʃ U _i = 0, где cos α ≠ 0

следовательно, предполагаемая равнодействующая R= 0.

Таким образом, система уравнений (1.6) показывает, что данная система сил не приводится ни к паре, ни к равнодействующей; следовательно, она уравновешивается. В случае если ось и перпендикулярна прямой АВ, то система уравнений (1.6) справедлива и при наличии равнодействующей, для которой АВ является линией действия. Пусть плоская система сил удовлетворяет трем уравнениям:

Ʃ M _iA=0; Ʃ M _iB=0; Ʃ M _iС=0

причем точки А, В и С не лежат на одной прямой. В этом случае силы не приводятся к паре сил, так как главные моменты этих сил относительно трех центров равны нулю. Силы не приводятся и к равнодействующей силе, так как если она существует, то линия ее действия не может пройти через три точки, не лежащие на одной прямой. Следовательно, рассматриваемая система сил уравновешивается, и система уравнений (1.7) является системой уравнений равновесия плоской системы сил.

Итак, установлено, что число уравнений равновесия плоской системы сил равно трем. При помощи этих уравнений можно решать задачи статики на плоскости, в которых число неизвестных не превышает трех.

Дата добавления: 2014-12-16