Уравнения движения точки в декартовых координатах

Координатный способ задания движения точки.

Векторный способ задания движения точки.

Естественный способ задания движения точки.

Тема 7. Кинематика точки.

Движущаяся точка описывает в пространстве некоторую линию.

Эта линия, представляющая собой геометрическое место последовательных положений движущейся точки в рассматриваемой системе отсчета, называется траекторией точка.

По виду траектории все движения точки делятся на прямолинейные и криволинейные.

Изучение движения точки заключается в определении основных характеристик этого движения: положения точки в выбранной системе отсчета, а также ее скорости и ускорения в любой момент времени. Эта задача решается различными способами.

Существуют три способа задания движения точки: естественный, векторный и координатный.

Рассмотрим естественный способ задания движения точки, применяемый в случае, когда траектория точки заранее известна. Траекторией может быть как прямая, так и кривая линия (рис. 167).

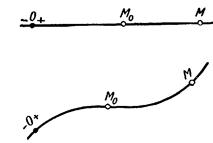
Рис 167.

Выберем на траектории неподвижную точку О, которую назовем началом отсчета дуговой координаты. Положение движущейся точки М на траектории будем определять дуговой координатой, т. е. расстоянием 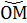= s, отложенным по траектории от начала отсчета О.

Расстояния, отложенные в одну сторону от точки О, будем считать положительными, а в противоположную — отрицательными, т. е. установим направление отсчета дуговой координаты. При движении точки М расстояние s от этой точки до неподвижной точки О изменяется с течением

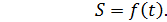(75.1)

Эта зависимость называется уравнением движения точки.

Если вид функции f (t) известен, то для каждого значения t можно найти значение s, отложить соответствующее расстояние по траектории и указать, где находится движущаяся точка М в этот момент времени.

Таким образом, движение точки определено, если известны следующие элементы: траектория точки, начало и направление отсчета дуговой координаты и уравнение движения s = f(t).

Дуговую координату точки не следует смешивать с длиной пути 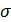, пройденного движущейся точкой. Дуговая координата s точки М в некоторый момент времени t может равняться пути 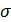, пройденному точкой за промежуток времени [0, t] только в том случае, если движение точки начинается из точки О и совершается в положительном направлении.

Если в начальный момент времени t₀ точка занимала положение М₀, а в момент времени t занимает положение М (рис. 167), то пройденный ею путь за промежуток [0, t] при движении точки в одном направлении определяется по формуле

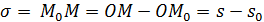. (75.2)

Изменение дуговой координаты s за элементарный промежуток времени dt равно дифференциалу дуги

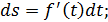
при движении точки в сторону возрастания дуг ds > 0; при движении точки в противоположную сторону ds < 0. Приращение пути 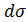(элементарное перемещение точки) всегда положительно, т. е.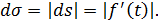

Путь, пройденный точкой за некоторый промежуток времени

[0, t], определяется как предел суммы элементарных перемещений

точки за этот промежуток времени:

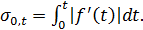(75.3)

Расстояние s и путь 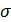выражаются в метрах.

Положение точки в пространстве однозначно определяется заданием радиуса вектора r, проведенного из некоторого неподвижного центра О в данную точку М (рис. 168).

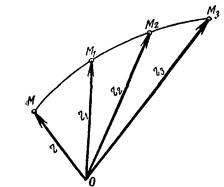
Рис 168.

Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор r, т. е. должна быть задана вектор-функция r аргумента t:

r = r (t). (76.1)

Траектория точки является геометрическим местом концов радиуса-вектора r движущейся точки.

Линия, образованная концами переменного вектора, начало которого находится в определенной точке пространства, называется годографом этого вектора. Следовательно, траектория точки М является годографом ее радиуса-вектора r.

Векторный способ определения движения материальной точки или системы материальных точек широко используется и в кинематике, и в динамике, так как он значительно упрощает многие выводы и иногда подчеркивает физическую сущность явлений.

От векторных формул легко перейти к аналитическим выражениям, обычно более удобным для вычислений.

Положение точки М в системе отсчета Oxyz определяется тремя декартовыми координатами точки х, у, z (рис. 169). При движении точки М ее координаты изменяются с течением времени. Следовательно, координаты х, у, z движущейся точки М являются функциями времени t:

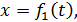
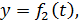(77.1)

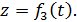
Эти уравнения называются уравнениями движения точки в декартовых координатах.

Уравнениями (77.1) определяется движение точки.

Действительно, имея эти уравнения, можно для каждого момента времени t найти соответствующие координаты х, у, z и по ним определить положение точки в пространстве в этот момент времени.

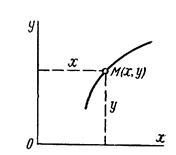
Рис 169 рис 170

Движение точки М в одной плоскости определяется двумя уравнениями движения (рис. 170):

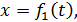
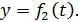(77.2)

Прямолинейное движение точки М (рис. 171) определяется одним

уравнением движения:

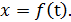(77.3)

В этом случае координатный способ задания движения точки сводится к естественному.

Уравнения движения, определяющие координаты точки в любой момент времени, можно рассматривать как параметрические уравнения траектории точки. При исключении параметра t из уравнений движения

Рис 171

получаются уравнения траектории точки в координатной форме. Пусть уравнения движения точки М имеют вид

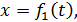
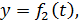
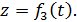
Решив первое уравнение относительно t, получим

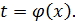
Подставив полученное для t выражение в два других уравнения, найдем уравнения траектории точки в координатной форме

. (77.4)

Как известно из аналитической геометрии, линии в пространстве соответствуют два уравнения с тремя координатами.

Пусть движение точки М в плоскости задано уравнениями

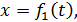
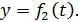
Исключив параметр t, получим уравнение траектории точки в координатной форме:

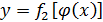. (77.5)

Помимо декартовых координат для определения положения точки на плоскости и в пространстве, применяют и другие системы координат (полярные, цилиндрические, сферические и др.).

Дата добавления: 2014-12-16