Системы механических единиц измерения

Для измерения механических величин применяются две системы единиц: физическая и техническая.

В физической системе механических единиц за основные единицы приняты единицы длины, массы и времени, а сила является величиной производной и имеет размерность:

.

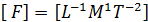В технической системе механических единиц за основные единицы приняты единицы длины, силы и времени, а масса является величиной производной и имеет размерность:

.

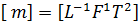В СССР в качестве государственного стандарта принята Международная система единиц измерения СИ (SI — от «Le systeme international d'unites)— в механике МКС, которая, так же как и система СГС, является физической системой единиц.

Система единиц измерения МКГСС является технической системой единиц.

За единицу массы в системе МКС принимается масса, равная одному килограмму (кг) платинового эталона, хранящегося в архиве Французской республики, а за единицу силы — ньютон (н) — сила, сообщающая массе 1 кг ускорение 1 м/сек².

1 ньютон = 10 дециньютонов (дн) = 100 сантиньютонов (сн) = 1000 миллиньютонов (мн).

1 килоньютон = 10 гектоньютонов (гн)— 10 деканьютонов (дан) = 1000 ньютонов.

В системе СГС за единицу массы принимается грамм (г), а за единицу силы — дина — сила, сообщающая массе 1 г ускорение 1 см/сек².

В системе МГКСС за единицу силы принимается килограммсила (кг с), сообщающая массе 1 кг ускорение 9,80665 м/сек².

За единицу массы в этой системе принимается техническая единица массы (т. е м.), т. е. масса, которой сила 1 кгс сообщает ускорение 1 м/сек ².

1 ньютон = 105 дин = 0,102 кгс

1 кгс =9,81 ньютона = 981000 дин.

1 т. е. м. = 9,81 кг.

Из второго закона следует, что если сила, действующая на точку, равна нулю, то и ускорение точки равно нулю, т. е. точка, не взаимодействующая с другими телами, или движется равномерно прямолинейно, или находится в покое.

Таким образом, первый закон динамики можно рассматривать как следствие более общего второго закона.

Система отсчета, в которой проявляются первый и второй законы, называется инерциальной системой отсчета. Для большинства задач за такую систему отсчета можно принять систему осей, связанных с Землей.

В случае, если необходимо учитывать суточное вращение Земли, за инерциальную систему отсчета принимают геоцентрическую систему осей координат с началом в центре Земли и осями, направленными к трем выбранным «неподвижным» звездам.

При решении астрономических задач пользуются гелиоцентрической системой осей координат с началом в центре Солнца и осями, направленными к трем выбранным «неподвижным» звездам. Эту систему с большей степенью точности можно принять за инерциальную систему.

Третий закон — закон равенства действия и противодействия двух тел отражает двусторонность механических процессов природы. Этот закон устанавливает, что при взаимодействии двух тел, в каком бы кинематическом состоянии они ни находились, силы, приложенные к каждому из них, равны по модулю и направлены по одной прямой в противоположные стороны. Будучи приложенными к разным телам, эти силы не уравновешиваются.

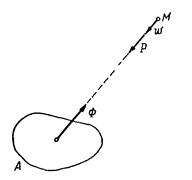
Рис 2.

Если, например, в результате механического взаимодействия некоторого тела А и материальной точки М массой т эта точка получает ускорение w (рис. 2), то сила Р, выражающая действие тела А на точку М, определяется вторым законом динамики:

.

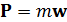По закону равенства действия и противодействия со стороны материальной точки М на тело А действует сила Ф, равная по модулю силе Р и направленная по той же прямой в противоположную сторону, т. е.

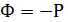
Или

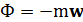. (2.6)

Модуль силы:

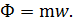(2.7)

Сила Ф, равная по модулю произведению массы материальной точки на модуль ее ускорения, направленная противоположно ускорению и приложенная к телу, сообщающему это ускорение, называется силой инерции материальной точки. При этом точка М и тело А могут не соприкасаться, тогда точка будет свободной (при действии сил тяготения или электростатических сил) или соприкасаться, тогда точка будет несвободной (наличие связи). Пусть, например, тело М лежит на гладкой горизонтальной плоскости, тогда вес его G уравновешивается реакцией плоскости N.

Если телу сообщают ускорение w при помощи нити А (рис. 3, а), действующей на тело с силой P = m w (рис. 3, б), то сила инерции Ф = -m w приложена к нити А (рис. 3, в). Эту силу ощущает человек, который тянет нить.

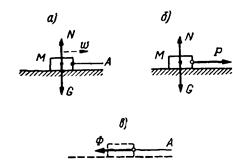
Рис 3.

Таким образом, сила инерции материальной точки является реальной силой, представляющей собой противодействие материальной точки изменению ее скорости, и приложена к телу, сообщающему этой точке ускорение.

При неравномерном криволинейном движении точки силу инерции Ф разлагают на две составляющие, направленные по касательной к траектории и по главной нормали (рис. 4).

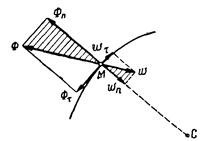
Рис 4.

Полученные составляющие 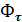и 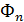называют касательной и нормальной силами инерции. Эти силы инерции направлены противоположно касательному и нормальному ускорениям. Поэтому имеем:

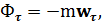
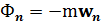. (2.8)

Из кинематики известно:

, ,

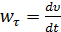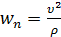где 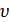— алгебраическая величина скорости точки; 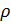— радиус кривизны траектории.

Пользуясь этими выражениями, получаем:

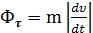, . (2.9)

Если точка М движется равномерно по кривой, 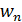= 0, = 0 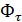и сила инерции Ф имеет лишь нормальную составляющую, а ее модуль

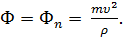
Если точка М движется неравномерно по прямой, то 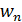= 0, = 0 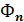и сила инерции Ф имеет лишь касательную составляющую, а ее модуль

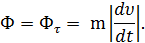
В случае равномерного прямолинейного движения точки w = 0, а потому и сила инерции равна нулю, т. е. Ф = 0.

Если точка М принадлежит твердому телу, вращающемуся вокруг неподвижной оси, то модули ее вращательного и центростремительного ускорений вычисляются по формулам:

, .

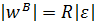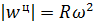где и 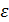— алгебраические значения угловой скорости и углового ускорения тела; R — расстояние от точки М до оси вращения.

Тогда модули касательной и нормальной сил инерции, называемых в этом случае вращательной и центробежной силами инерции, определяются по формулам:

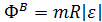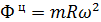, . (2.10)

При равномерном вращении тела 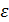= 0 Ф ^в = 0, сила инерции

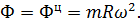
Сила инерции является одним из важнейших понятий динамики. Действие сил инерции учитывается при решении многих технических задачи, в частности, при определении реакций связей движущейся несвободной механической системы.

Четвертый — закон независимости действия сил — не был сформулирован Ньютоном как отдельный закон механики, но он содержится в сделанном им обобщении правила параллелограмма сил.

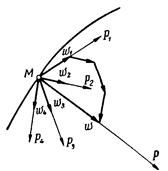
Рис 5.

Положим, что на материальную точку М действуют силы Р₁, P₂ , P₃, …, P_n (рис. 5). Каждая из этих сил, действуя на материальную точку отдельно, сообщает ей ускорения w₁, w₂, …, w_n, определяемые по второму закону:

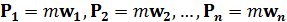
Согласно четвертому закону, ускорение материальной точки, находящейся под действием сил Р₁, P₂ , P₃, …, P_n,определяется уравнением:

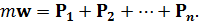
Если принять ускорение w, получаемое материальной точкой под действием всей системы одновременно действующих на нее сил, равным геометрической сумме составляющих ускорений, т. е.

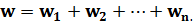
то, умножив обе части этого равенства на m, получим:

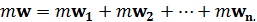
Или

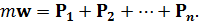
Таким образом, закон независимости действия сил равносилен утверждению, что ускорение w, получаемое материальной точкой от одновременно действующей на нее системы сил, равно геометрической сумме ускорений w₁, w₂, …, w_n, сообщаемых этой точке каждой из сил в отдельности.

Четвертый закон, так же как и остальные законы классической механики, подтверждается опытами и наблюдениями.

Дата добавления: 2014-12-16