Вспомогательные теоремы для определения положения центра тяжести

При вычислении координат центров тяжести пользуются различными приемами, позволяющими упростить вычисления. Рассмотрим четыре вспомогательные теоремы, упрощающие в некоторых случаях нахождение центров тяжести.

Теорема 1. Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Рассмотрим однородное тело, имеющее ось симметрии (рис. 145).

Рис 145

Совместим с осью симметрии одну из осей координат, например ось z, и определим две координаты центра тяжести однородного тела по формулам (66.2):

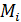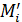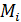Возьмем в этом теле любые две точки и расположенные симметрично относительно оси z. Выделим около них равные элементарные объемы . Точки . и 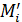лежат на одном перпендикуляре к оси z, на равных расстояниях от этой оси, т. е.

(рис. 145). Следовательно, координаты 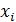и 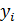этих точек равны по величине и противоположны по знаку. Разбив все тело на пары симметрично расположенных и равных элементарных объемов, составляем произведения 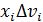и суммируем их. Сумма слагаемых, относящихся к одной паре, равна нулю, так как объемы равны, а координаты 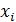равны по величине, но имеют противоположные знаки.

Из этого следует, что равна нулю и сумма, содержащая все элементарные объемы тела, т. е. 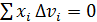и аналогично .

Подставив эти значения в формулы (66.2), получим:

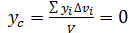
Так как и , то центр тяжести тела лежит на оси z, являющейся осью симметрии тела, и его положение на этой оси определяется лишь одной координатой:

.

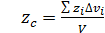Применяя эту теорему к плоской фигуре или линии, легко установить, что если плоская фигура или линия имеет ось симметрии, то ее центр тяжести лежат на этой оси.

Дата добавления: 2014-12-16