Определение положения центра тяжести плоской фигуры по центрам тяжести ее частей. Способ отрицательных площадей

Теорема 4. Площадь поверхности вращения, полученной вращением плоской кривой вокруг оси, лежащей в плоскости этой кривой, но ее не пересекающей, равна произведению длины, этой кривой на длину окружности, описанной ее центром тяжести.

Теорема 3. Объем тела вращения, полученного вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, но не пересекающей ее, равен произведению площади фигуры на длину окружности, описанной ее центром тяжести.

Пусть плоская фигура площадью F вращается вокруг оси у, лежащей в плоскости фигуры и не пересекающей ее. При вращении вокруг оси у контур этой фигуры описывает некоторую замкнутую поверхность, называемую поверхностью вращения. Тело, ограниченное этой поверхностью, называется телом вращения (рис. 147).

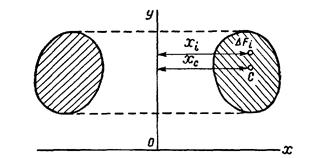
Рис 147.

Объем этого тела вращения определим, как сумму бесконечно большого числа объемов элементарных круговых колец, образованных вращением вокруг оси у бесконечно малых площадок 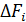. Радиус каждого кольца равен расстоянию этой площадки от оси у, т. е. координате .

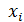Объем элементарного кольца

,

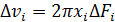Объем тела вращения

Здесь суммирование распространено на все площадки, входящие в состав данной площади F.

Сумму 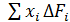можно определить из формулы (67.1):

.

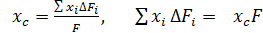Подставив это значение в выражение, определяющее объем тела вращения, получим:

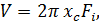(69.1)

где 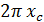— длина окружности, описанной центром тяжести фигуры.

Пусть кривая АВ длиной L вращается вокруг оси у, лежащей в плоскости этой кривой, но не пересекающей ее. При вращении вокруг оси у эта кривая опишет некоторую поверхность вращения (рис. 148).

Разобьем кривую на бесчисленное множество бесконечно малых элементов длиной 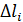. Поверхность, описанную каждым элементом, можно принять за поверхность усеченного конуса. Как известно из геометрии, площадь боковой поверхности усеченного конуса равна произведению-длины окружности среднего сечения на длину образующей. Поэтому площадь поверхности, образованной вращением элемента кривой 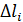можно определить по формуле

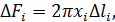
где 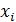— радиус окружности, равный расстоянию середины элемента от оси у.

Площадь поверхности вращения

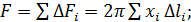
здесь суммирование распространено на все элементы 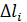кривой АВ.

Сумму 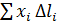определим из формулы (68.1):

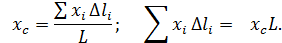
Подставив это значение в выражение, определяющее площадь поверхности вращения, получим

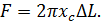(69.2)

Пусть требуется определить положение центра тяжести некоторой плоской фигуры, состоящей из трех частей, положение центров тяжести которых известно (рис. 149).

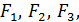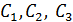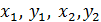Положим, что площади частей фигуры соответственно равны а координаты их центров тяжести будут и .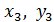

Рис 149 Рис 150.

Статические моменты площади плоской фигуры относительно осей координат равны суммам статических моментов площадей отдельных ее частей, которые можно определить по формулам (67.2):

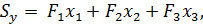
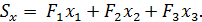
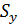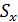Определив статические моменты и плоской фигуры, можно найти координаты ее центра тяжести С по формулам (67.3):

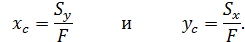
Подставив значения статических моментов, получаем:

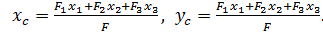(70.1)

Этот способ удобно применять и центра тяжести плоской фигуры, из часть (рис. 150). Зная величину Fx площади фигуры с контуром А и координаты

Зная величину 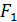площади фигуры с контуром А и координаты 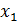и 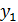ее центра тяжести 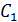а также площадь 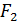части, вырезанной по контуру В, и координаты 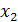и 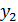ее центра тяжести 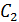, можно вычислить координаты центра тяжести оставшейся части фигуры по формулам, аналогичным формулам (70.1). При этом площадь оставшейся части должна быть равна разности площаде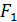й и 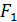, а ее статические моменты — разности статических моментов площадей фигур А и В. Тогда

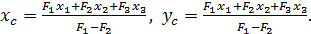(70.2)

Этот способ определения центра тяжести плоской фигуры, из которой вырезана некоторая часть, называется способом отрицательных площадей.

Аналогичный прием, называемый способом о трицательных объемов, применяется при вычислении координат центра тяжести однородного тела, полученного вырезанием из тела объемом 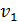, с центром тяжести 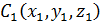, части объемом 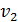, с центром тяжести 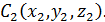Тогда

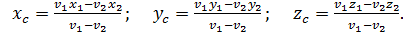(70.3)

Дата добавления: 2014-12-16