Площадь плоских сечений

Тема 2. Геометрические характеристики плоских сечений.

Если в некотором положении механической системы с двусторонними идеальными связями приложенные к ней силы уравновешиваются, то на любом возможном перемещении системы из этого положения сумма работ задаваемых сил равна нулю.

В случае односторонних связей уравнение (114.2) остается справедливым лишь в случае, когда возможные перемещения являются неосвобождающими. В общем же случае при односторонних связях

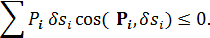
Если в каждую точку 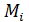системы из некоторого центра О провести вектор r _i, то возможное перемещение этой точки 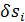будет соответствующим возможным приращением радиуса-вектора точки:

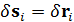(i= 1, 2, …, n).

Тогда уравнение работ (114.2) примет вид:

. (114.3)

Как уже известно, при растяжении и сжатии прочность и жёсткость стержней, напряжения, возни­кающие в их поперечных сечениях, потенциальная энергия деформации и другие зависят от площадей поперечных сечений стержней.

Площадь является простейшей геометрической характеристикой поперечного сечения (рис. 2.1). Если представить сечение состоящим из бесчисленного множества элементарных площадок dF, то площадь всего сечения

(2.1)

При расчётах на изгиб, кручение, сложное сопротивление, а также при расчётах сжатых стержней на устойчивость используются более сложные геометрические характеристики сечений: статический момент, а также осевой (или экваториальный), полярный и центробежный моменты инерции сечений. Выражения этих характеристик отличаются от выражения (2.1) тем, что у них под знаки интеграла вхо­дят произведения элементарных площадок dF на функции координат Y, X, этих площадок (рис. 2.1). Та­ким образом, указанные геометрические характеристики зависят не только от формы и размеров сече­ния, но также от положения осей и точек (полюсов), относительно которых они вычисляются.

Геометрические характеристики сечений простой формы можно определить по специальным фор­мулам. Кроме того, в таблицах ГОСТ (называемых также таблицами нормального сортамента) приво­дятся геометрические характеристики профилей стандартного проката (уголков, швеллеров, двутавров). Для определения геометрических характеристик сложных сечений приходится расчленять их на ряд простых фигур и пользоваться формулами, устанавливающими зависимости между геометрическими характеристиками относительно различных осей.

Рис. 2.1. Площадь сечения

Дата добавления: 2014-12-16