Первая гипотеза прочности

Первая гипотеза прочности называется также гипотезой наибольших нормальных напряжений, по­тому что за критерий прочности она принимает наибольшее нормальное напряжение. Сформулирована она может быть следующим образом: предельное состояние материала при сложном напряжённом со­стоянии наступает тогда, когда наибольшее нормальное напряжение достигает величины предельного напряжения при одноосном напряжённом состоянии.

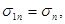
где 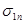- предельное значение наибольшего (из трёх) нормального напряжения (в момент разрушения); 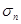- предельное напряжение при одноосном сжатии или растяжении (предел прочности).

Диаграмма предельных напряжений по первой гипотезе изображена на рис. 3.3, а в виде прямых 1-2, 2-3, 3-4 и 1-4. При этом отрезки ОА = OF представляют собой предельное напряжение при одноосном растяжении, отрезки ОВ= ОК- предельное напряжение при одноосном сжатии. Для хрупких материалов ОВ > OF, для пластичных материалов ОВ= OF (рис. 3.3, б). Разделив обе части равенства на коэффици­ент запаса прочности и добавляя знак неравенства, получим условие прочности

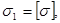
где 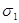- фактическое значение наибольшего главного напряжения, возникающего в опасной точке дета­ли; 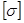- допускаемое значение нормального напряжения, принимаемое для одноосного растяжения или сжатия.

Первую гипотезу прочности можно сформулировать также следующим образом: прочность мате­риала при сложном напряжённом состоянии обеспечивается, если наибольшее нормальное напряжение не превосходит допускаемого нормального напряжения, установленного для одноосного напряжённого состояния.

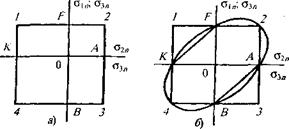
Рис. 3.3. Диаграмма предельных напряжений

Как видим, эта гипотеза учитывает лишь влияние наибольшего главного напряжения, пренебрегая влиянием двух других главных напряжений на прочность материала. Рассмотренные выше опыты для пластичных материалов не подтверждают этой гипотезы как гипотезы пластичности, т.е. гипотезы, ус­танавливающей критерий возникновения текучести. Опытные точки располагаются не на прямых FC, СЕ и BE, как это следует из первой гипотезы, а на некоторой кривой линии CKADB.

Для хрупких материалов в I квадранте диаграммы предельных напряжений и в значительной части IV (или //) квадранта первая гипотеза хорошо согласуется с опытными данными. В этих случаях ею и следует пользоваться, рассматривая её как гипотезу, устанавливающую критерий хрупкого разрушения.

Если материал имеет различные допускаемые напряжения на растяжение и сжатие, то вместо одно­го условия прочности будем иметь два условия - по наибольшим растягивающим и сжимающим на­пряжениям:

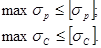
Дата добавления: 2014-12-16