Главные оси и главные моменты инерции

Рис. 2.4. Сечение произвольного очертания

Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения х и у к положению и и к Из (рис 2.4) легко установить, что

(2.10)

Из выражений

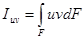
с учетом (2.10) после несложных преобразований получим:

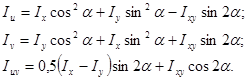(2.11)

Складывая первые два уравнения, получим

I_u + I_v = I_x + I_у = I_ρ,

где ρ² = x² + y²; I_р — полярный момент инерции сечения, величина которого, как видно, не зависит от уг­ла поворота координатных осей.

Приравняв значение I_и к нулю, находим положение главных центральных осей, при котором функция I_и принимает экстремальное значение:

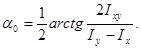(2.13)

С учётом (2.12) можно утверждать, что при α = α₀ один из осевых моментов I_u или I_v будет наи­большим, а другой наименьшим. Положительное направление угла α₀ откладывается против хода часо­вой стрелки.

Декартовы оси координат, относительно которых осевые моменты инерции принимают экстре­мальные значения, называются главными осями инерции. Осевые моменты инерции относительно глав­ных осей называются главными и находятся по формулам (2.11) или (2.14):

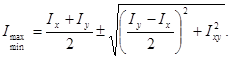(2.14)

Дата добавления: 2014-12-16