Статические моменты инерции сечений

Статическим моментом сечения относительно некоторой оси называется взятая по всей его площа­ди F сумма произведений элементарных площадок dF на их расстояния от этой оси, т.е.

(2.2)

Статические моменты выражаются в см³, м³ и т.д.

Статический момент сложного сечения относительно некоторой оси равен сумме статических мо­ментов всех частей этого сечения относительно той же оси.

Нельзя суммировать статические моменты частей сечения, вычисленные относительно различных осей. Изменение положительного направления оси у вызывает изменение знака статического момента S _x; аналогично, изменение положительного направления оси х вызывает изменение знака статического момента S_y.

Установим зависимость между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей и x₁ (рис. 2.2). Выражения статических моментов относительно этих осей на основании формулы (2.2) имеют вид

но y₁ = (y-a) и следовательно,

Рис. 2.2. Сечение

Окончательно

(2.3)

и, аналогично,

(2.4)

Найдём теперь положение осей х₁ и у₁, относительно которых статические моменты равны нулю. Для этого приравняем нулю выражения (2.3) и (2.4):

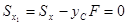
Откуда

(2.5)

Оси, проходящие через центр тяжести, называются центральными осями. Относительно любой оси, проходящей через центр тяжести сечения (т.е. относительно любой центральной оси), статический мо­мент равен нулю. Формулы (2.5) используются для определения координат центра тяжести сечения.

Для случаев, когда положение центра тяжести сечения известно, а требуется определить статиче­ские моменты сечения относительно любых осей у и х, формулы (2.5) преобразуются к виду

(2.6)

На основании вышеизложенного можно установить следующий порядок определения положения центра тяжести сложного сечения:

1. Сложное сечение разбивается на части, имеющие вид простых фигур.

2. Определяются площади и положения центров тяжести каждой фигуры.

3. Выбираются случайные координатные оси у их.

4. По формулам (2.6) вычисляются статические моменты и каждой фигуры относительно осей у и х. Затем путём суммирования значений определяется статический момент S_y, а значений - статический момент S_x всего сечения.

5. По формулам (2.5) вычисляются координаты центра тяжести всего сечения.

В отдельных случаях, когда заданное сечение нельзя разбить на такие фигуры, положение центров тяжести которых известны, положение центра тяжести всего сечения необходимо определить путём не­посредственного интегрирования.

Дата добавления: 2014-12-16