Моменты инерции сечения

Осевым {или экваториальным) моментом инерции сечения относительно некоторой оси называется взятая по всей его площади F сумма произведений элементарных площадок dF на квадраты их расстоя­ний от этой оси, т.е.

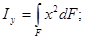
(2.7)

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей его площади F сумма произведений элементарных площадок dF на квадраты их расстояний от этой точки, т.е

(2.8)

Центробежным моментом инерции сечения относительно некоторых двух взаимно перпендикуляр­ных осей называется взятая по всей его площади F сумма произведений элементарных площадок dF на их расстояния от этих осей, т.е.

(2.9)

Моменты инерции выражаются в см⁴, м⁴ и т.д. Осевые и полярные моменты инерции всегда поло­жительны, так как в их выражения под знаки интегралов входят величины площадок dF (всегда поло­жительные) и квадраты расстояний этих площадок от данной оси или полюса.

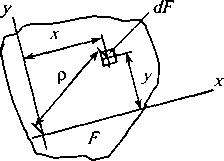На рисунке 2.3 изображено сечение площадью F и показаны оси у и x.

Рис. 2.3. Сечение площадью F.

Осевые моменты инерции этого сечения относительно осей у и x:

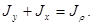
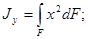
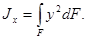
Сумма этих моментов инерции

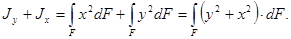
Но

,

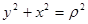следовательно,

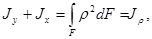
т.е.

Сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей рав­на полярному моменту инерции этого сечения относительно точки пересечения указанных осей.

Центробежные моменты инерции могут быть положительными или равными нулю. Центробежный момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симмет­рии, равен нулю. Осевой момент инерции сложного сечения относительно некоторой оси равен сумме осевых моментов инерции составляющих его частей относительно этой же оси. Аналогично, центро­бежный момент инерции сложного сечения относительно любых двух взаимно перпендикулярных осей равен сумме центробежных моментов инерции составляющих его частей относительно этих же осей. Также и полярный момент инерции сложного сечения относительно некоторой точки равен сумме по­лярных моментов инерции составляющих его частей относительно той же точки. Следует иметь в виду, что нельзя суммировать моменты инерции, вычисленные относительно различных осей и точек.

Для прямоугольника

Для круга

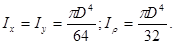
Для кольца

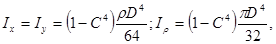
Где

Часто при решении практических задач необходимо определять моменты инерции сечения относи­тельно осей, различным образом ориентированных в его плоскости. При этом удобно использовать уже известные значения моментов инерции всего сечения (или отдельных составляющих его частей) отно­сительно других осей, приводимые в технической литературе, специальных справочниках и таблицах, а также подсчитываемые по имеющимся формулам. Поэтому очень важно установить зависимости между моментами инерции одного и того же сечения относительно разных осей.

В самом общем случае переход от любой старой к любой новой системе координат может рассмат­риваться как два последовательных преобразования старой системы координат:

1) путём параллельного переноса осей координат в новое положение;

2) путём поворота их относительно нового начала координат.

Следовательно,

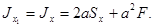
Если ось х проходит через центр тяжести сечения, то статический момент S_x = 0 и

Из всех моментов инерции относительно параллельных осей осевой момент инерции имеет наи­меньшее значение относительно оси, проходящей через центр тяжести сечения.

Момент инерции относительно оси у

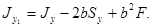
В частном случае, когда ось / проходит через центр тяжести сечения,

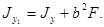
Центробежный момент инерции

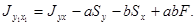
В частном случае, когда начало старой системы координат y0х находится в центре тяжести сечения,

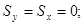
Если сечение симметрично и одна из старых осей (или обе) совпадают с осью симметрии, то

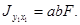
Дата добавления: 2014-12-16