Центр тяжести линии

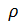Определим положение центров тяжести однородных тел, имеющих большую протяженность при сравнительно малой площади поперечного сечения. Рассмотрим, например, кусок однородной тонкой проволоки постоянного сечения, ось которой расположена по дуге кривой AB (рис. 144). Вес проволоки выразим формулой где L — длина линии АВ, — вес единицы длины проволоки. Разобьем линию АВ на элементарные участки 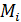длиной 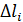. Вес каждого участка определится по формуле:

Координаты центра тяжести элементарного участка обозначим х_i, y_i, z_i. Тогда координаты центра тяжести С рассматриваемого куска проволоки определятся по формулам (66.1):

Или

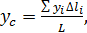(68.1)

где суммирования распространены на все элементы проволоки. Формулы (68.1) показывают, что координаты центра тяжести не зависят от постоянной 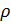, характеризующей вещество проволоки.

Центр тяжести однородной тонкой проволоки постоянного сечения, ось которой совпадает с некоторой линией, называется центром тяжести этой линии.

Дата добавления: 2014-12-16