Метод вырезания узлов

Расчет плоских ферм.

Тема 5.Расчет ферм.

Цели и задачи изучения темы:

Результат освоения темы:

Индекс компетенции	Индекс образовательного результата	Образовательный результат

Пример решения задач на равновесие системы тел дает расчет ферм. Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферму называют плоской.

Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня.

Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Ограничимся рассмотрением жестких плоских ферм без лишних стержней, образованных из треугольников. В таких фермах число стержней k и число узлов п связаны соотношением k = 2п - 3.

В самом деле, в жестком треугольнике, образованном из трех стержней, будет три узла (см., например, ниже на (рис. 1.1.60) треугольник АВD, образованный стержнями 1, 2, 3). Присоединение каждого следующего узла требует два стержня (например, на (рис. 1.1.60) узел С присоединен стержнями 4, 5, узел Е – стержнями 6, 7, и т. д.); следовательно, для всех остальных (п - 3) узлов потребуется 2(n - 3) стержней. В результате число стержней в ферме k = 3+2(n - 3)=2 n - 3. При меньшем числе стержней ферма не будет жесткой, а при большем числе она будет статически неопределимой.

Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях.

Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Перейдем к определению усилий в стержнях.

Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий сил, сходящихся в каждом из узлов. Ход расчетов поясним на конкретном примере.

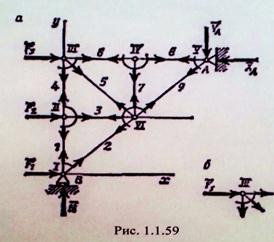
Рассмотрим изображенную на (рис. 1.1.59), а ферму, образованную из одинаковых равно­бедренных прямоугольных треугольников; действующие на ферму силы параллельны оси x и численно равны:

F₁=F₂=F₃=20кH

В этой ферме число узлов n = 6, а число стержней k= 9. Следовательно, ферма является жесткой без лишних стержней.

Составляя уравнения равновесия для фермы в целом, найдем, что реакции опор на­правлены, как показано на рисунке, и численно равны:

X_A = 3F=60 kH, Y_A=N= 3F/2=30кН.

Переходим к определению усилий в стержнях. Пронумеруем узлы фермы римскими цифрами, а стержни - арабскими. Искомые усилия обозначим S₁ (в стержне 1), S₂ (в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от остальной фермы. Действие отброшенных стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S₁, S₂,…

Изображаем сразу все эти силы па рисунке, направляя их от узлов, т. е. считая все стержни растянутыми (рис. 1.1.59, а; изображенную картину надо представить себе для каж­дого узла гак, как это показано на рис. 1.1.59, б для узла III). Если в результате расчета зна­чение усилия в каком-нибудь стержне получится отрицательным, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, на рис. 1.1.59 не вводим, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно S₁, вдоль стержня 2 - равны S₂ и т. д.

Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия:

ƩF_kx = 0, Ʃ F_ky = 0.

(Рис. 1.1.59) начинаем с узла I, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия. Составляя уравнения равновесия для узла I, получим:

F₁ + S₂ соs 45° = 0 N + S₁ +S₂ sin 45° = 0.

Отсюда находим:

S₂ = -F 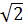= -28,2 кН, S ₁ = = - = -10 кН.

Теперь, зная S₁, переходим к узлу II. Для него уравнения равновесия дают S₃ + F₂=0, S ₄ – S₁ = 0, откуда

S₃ = -F = -20 кН, S₄=S₁= -10 кН.

Определив S₄, составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:

S₅ = - S₄ 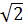= 14,1 кН, S₆ = S₈= -30 кН, S₇ = 0.

Наконец, для вычисления S₉ составляем уравнения равновесия сил, сходящихся в узле V, проектируя их ось на ось B y. Получим Y _A+S₉ cos 45^o=0, откуда S₉= - = -42.3 кH.

Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как проверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при опре­делении N, Х_A и Ya.

Окончательные результаты расчета можно свести в таблицу:

Как показывают знаки усилий, стержень 5 растянут, остальные стержни сжаты; стер­жень 7 не нагружен (нулевой стержень).

Наличие в ферме нулевых стержней, подобных стержню 7, обнаруживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную упомянутым двум стержням. Например, в ферме, изображенной на рис. 1.1.60, при отсутствии силы Р₄ нулевым будет стержень 15, а следовательно, и 13. При наличии же силы Р₄ ни один из этих стержней нулевым не является.

Если в ходе расчета встретится узел, для которого число неизвестных больше двух, то можно воспользоваться методом сечений.

Дата добавления: 2014-12-16