Момент силы и главный момент системы сил, лежащих в одной плоскости. Теорема о сумме моментов сил, составляющих пару

Зависимость между главными моментами системы сил относительно точки и оси, проходящей через эту точку.

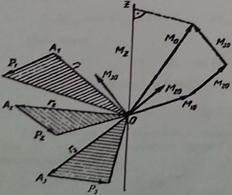
Рис. 46

На (рис. 46) изображен многоугольник моментов сил ₁, ₂ и ₃ относительно точки О. Проведем через эту точку произвольную ось z и спроецируем на эту ось главный момент _O, а также моменты _Ю, ₂₀, 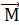_nO. Тогда

М₀ cos ( _O ,z) = М_1O cos( _1O,z) + ₂₀ соs ( ₂₀, z) + _3O соs ( _3O, z).

Отсюда

М_1O cos( _1O,z)= M_1z; ₂₀ соs ( ₂₀,z)=M_2z; _3O соs ( _3O, z)=M_3z.

Получаем

М₀ cos ( _O ,z) = M_1z+M_2z+M_3z =M_z.

Распространяя эту зависимость на любое число сил, получаем

М₀ cos ( _O ,z)=ƩM_iz =M_z.

Таким образом, проекция главного момента системы сил относительно некоторой точки на ось, проходящую через эту точку, равна главному моменту системы сил относительно этой оси.

Если рассматриваются только силы, лежащие в одной плоскости, то их моменты относительно точек этой плоскости должны быть направлены по перпендикулярам к этой плоскости в ту или иную сторону. Поэтому моменты сил относительно точки плоскости тождественны их моментам относительно оси, проходящей через эту точку перпендикулярно плоскости расположения сил (рис. 47, а, б).

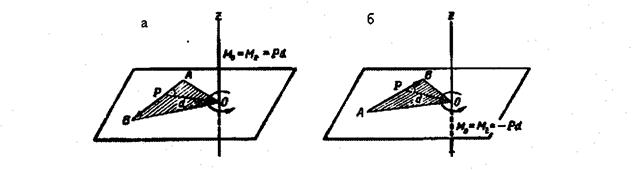
Рис. 47

Моменты сил относительно точки плоскости следует рассматривать как алгебраические величины (не векторы). Плоскость расположения сил обычно изображают плоскостью чертежа.

Таким образом, моментом силы относительно некоторой точки О на плоскости называется алгебраическая величина, равная произведению модуля силы на ее плечо d относительно этой точки (рис. 48):

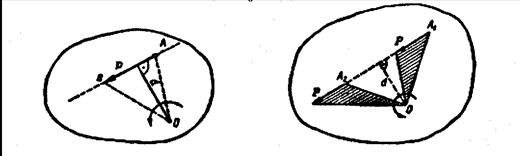
Рис. 48 Рис. 49

Момент силы относительно точки считается положительным, если сила стремится повернуть плоскость чертежа вокруг точки О в сторону, противоположную вращению часовой стрелки, и отрицательным, если в сторону вращения часовой стрелки.

Момент силы относительно точки можно определить удвоенной площадью треугольника АОВ:

M₀=±2×S_ΔА0В

За единицу момента принимается 1 Н^.м.

При переносе вдоль линии ее действия момент силы относительно данной точки плоскости не изменяется (рис. 49). Момент силы Р относительно данной точки О равен нулю, если линия действия силы проходит через эту точку, т. е. d= 0 (рис. 50).

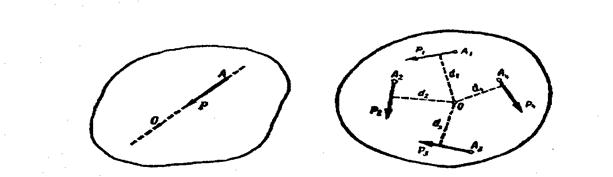
Рис. 50 Рис. 51

Если к твердому телу приложено несколько сил, лежащих в одной плоскости, можно вычислить алгебраическую сумму моментов этих сил относительно любой точки этой плоскости (рис. 51):

Момент Мо, равный алгебраической сумме моментов данной системы сил относительно какой-либо точки в той же плоскости, называют главным моментом системы сил относительно этой точки:

М₀=М_ю+М₂₀+... + М_n0 или M ₀=Ʃ M₁₀

Основываясь на понятии главного момента системы сил относительно точки на плоскости, сформулируем теорему о моменте пары сил на плоскости: главный момент сил, составляющих пару относительно произвольной точки на плоскости действия пары, не зависит от положения этой точки и равен моменту этой пары сил (рис. 52).

М₀=±Pd=М.

Как видно, главный момент сил, составляющих пару относительно произвольной точки на плоскости ее действия, так же как и главный момент сил пары относительно точки в пространстве, является величиной, не зависящей от выбора этой точки.

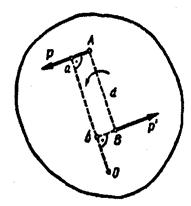
Рис. 52

Дата добавления: 2014-12-16