
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сложение двух сходящихся сил. Параллелограмм и треугольник сил
|
|
|
|
Тема 2. Система сходящихся сил.
Цели и задачи изучения темы:
Результат освоения темы:
| Индекс компетенции | Индекс образовательного результата | Образовательный результат |
Сходящимися называются силы, линии действия которых пересекаются в одной точке.
Если к телу приложены две силы, линии действия которых пересекаются в одной точке, то, как указывалось в аксиоме параллелограмма сил, их равнодействующая приложена в точке А пересечения линий действия сил; она изображается диагональю параллелограмма, построенного на этих силах (рис. 19). Построение параллелограмма сил можно заменить построением треугольника сил ABD (рис. 20).
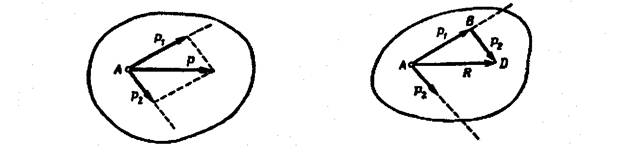
Рис. 19 Рис. 20
Направление равнодействующей силы 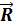 по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому слагаемыми силами.
по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому слагаемыми силами.
При помощи параллелограмма или треугольника сил можно решить и обратную задачу — разложить силу  на две составляющие
на две составляющие 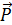 1,
1,  2, приложенные в той же точке и направленные по заданным линиям действия KL и DE (рис. 21) и (рис. 22).
2, приложенные в той же точке и направленные по заданным линиям действия KL и DE (рис. 21) и (рис. 22). 
Рис. 21 Рис. 22
Используя известные формулы тригонометрии (теорему синусов), имеем 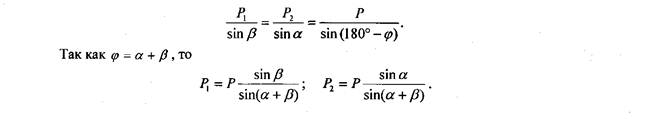
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1964; Нарушение авторских прав?; Мы поможем в написании вашей работы!