Завдання. Теорема про три моменти

Теорема про три моменти.

Плоска система сил

Умови рівноваги плоскої системи сил

На тіло діє плоска система сил. Розташуємо осі Ox і Oy в площині дії сил.

Рівняння .

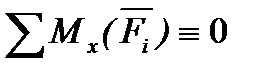
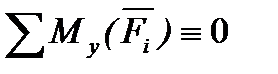Для рівноваги плоскої системи сил, що діють на тверде тіло, необхідно і достатньо, щоб суми проекцій цих сил на кожну з двох прямокутних осей координат, розташованих у площині дії сил, дорівнювали нулю і сума моментів цих сил відносно будь-якої точки, що знаходиться в площині дії сил також дорівнювала нулю.

, , .

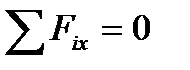Для рівноваги плоскої системи сил, що діють на тверде тіло, необхідно й достатньо, щоб суми моментів цих сил системи відносно трьох будь-яких точок, розташованих у площині дії сил, і таких, що не лежать на одній прямій, дорівнювали нулю:

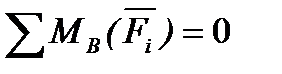
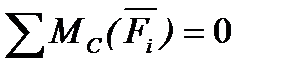
Статично визначувані та статично невизначувані

Для будь-якої плоскої системи сил, що діють на тверде тіло, є три незалежні умови рівноваги. Отже, для будь-якої плоскої системи сил з умов рівноваги можна знайти не більше трьох невідомих. У разі просторової системи сил, що діють на тверде тіло, є шість незалежних умов рівноваги. Отже, для будь-якої просторової системи сил з умов рівноваги можна знайти не більше шести невідомих.

Завдання, в яких число невідомих не більше числа незалежних умов рівноваги для даної системи сил, прикладених до твердого тіла, називаються статично визначувані.

Інакше завдання статично невизначувані.

Рівновага системи тіл

Розглянемо рівновагу сил, прикладених до системи тіл, що взаємодіють між собою. Тіла можуть бути сполучені між собою за допомогою шарнірів або іншим способом.

Сили, що діють на дану систему тіл, можна розділити на зовнішні та внутрішні.

Зовнішніми називаються сили, з якими на тіла даної системи діють тіла, що не входять в цю систему сил.

Внутрішніми називаються сили взаємодії між тілами даної системи.

При розгляді рівноваги сил, прикладених до системи тіл, можна подумки розчленувати систему тіл на окремі тверді тіла і до сил, що діють на ці тіла, застосувати умови рівноваги, отримані для одного тіла. До цих умов рівноваги ввійдуть як зовнішні, так і внутрішні сили системи тіл. Внутрішні сили на підставі аксіоми про рівність сил дії і протидії в кожній точці зчленування двох тіл утворюють рівноважну систему сил.

Покажемо це на прикладі системи двох тіл і плоскої системи сил.

Якщо скласти умови рівноваги для кожного твердого тіла системи тіл, то для тіла 1 :

,

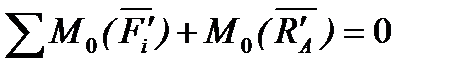для тіла 2

.

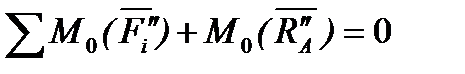Крім того, з аксіоми про рівність сил дії та протидії для двох взаємодіючих тіл маємо

.

Наведені рівності і є умовами рівноваги зовнішніх сил, що діють на систему.

Реакція защемлення

Розглянемо балку, один кінець якої АВ закладений у стіну. Таке кріплення кінця балки АВ називається защемленням у точці В Хай на балку діє плоска система сил. Визначимо сили, які треба прикласти до точки В балки, якщо частину балки АВ відкинути. До перетину балки (В) прикладені розподілені сили реакції. Якщо ці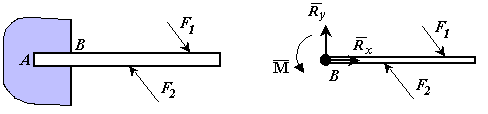

Рисунок 5.2

сили замінити елементарними зосередженими силами і потім привести їх до точки В, то в точці В отримаємо силу 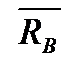(головний вектор сил реакції) і пару сил з моментом М (головний вектор сил реакції відносно точки В). Момент М називають моментом защемлення, або реактивним моментом. Силу реакції 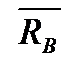можна замінити двома складовими 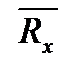і .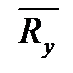

Защемлення на відміну від шарніра створює не лише невідому за величиною і напрямком реакцію 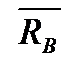, але ще і пару сил із невідомим моментом М у защемленні.

Лекція 6

Короткий зміст: Центр паралельних сил. Паралельні сили розподілені по відрізку прямої. Центр ваги твердого тіла, поверхні та лінії. Способи визначення координат центра ваги.

Дата добавления: 2014-12-16