
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторное произведение
|
|
|
|
10 Векторным произведением вектора 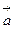 , на вектор
, на вектор 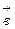 называется вектор
называется вектор  , такой что:
, такой что:
1) длина вектора  равна
равна 

 где
где 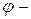 угол между векторами, т.е. длина вектора
угол между векторами, т.е. длина вектора  равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах 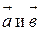 .
.
2) Вектор  , перпендикулярен каждому из векторов
, перпендикулярен каждому из векторов 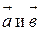 .
.
3) Векторы  образуют правую тройку векторов, т.е. кратчайший поворот вектора
образуют правую тройку векторов, т.е. кратчайший поворот вектора 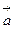 в сторону вектора
в сторону вектора 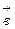 виден из точек
виден из точек  совершающимся против часовой стрелки.
совершающимся против часовой стрелки.
Векторное произведение обозначается 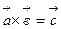 .
.
20 Свойства векторного произведения:
1) 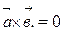 , если
, если 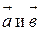 - коллинеарные векторы (т.е. параллельные одной прямой)
- коллинеарные векторы (т.е. параллельные одной прямой)
2) 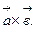 =
=  .
.
3) 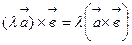
4) 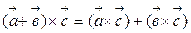 .
.
30 

 ,
,  ,
, 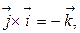
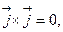
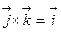 ,
,  ,
,  ,
, 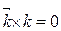 .
.
40 Выражение векторного произведения через координаты сомножителей: 
 .
.
|
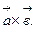 =
= 
Эту формулу с помощью определителей второго порядка можно записать в виде:
|
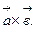 =
= 
50 Площадь параллелограмма построенного на векторах  :
:
S= 
И площадь треугольника построенного на векторах 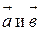 :
:
S= 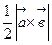
Пример 8. Даны векторы 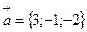 ,
, 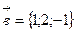 .
.
Найти: 1) 
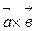 , 2)
, 2) 
Решение. 1) Находим векторное произведение 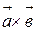 .
.
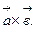 =
= 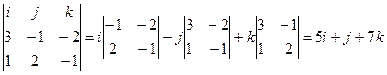 .
.
2) Найдём координаты вектора 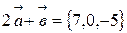 и находим векторное произведение
и находим векторное произведение  и
и 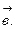
 .
.
Ответ: 
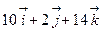 .
.
Пример 9. Вычислить площадь параллелограмма, построенного на векторах 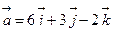 и
и 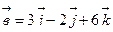 .
.
Решение. Находим векторное произведение 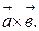 :
:
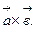 =
=  .
.
 Ответ: S=49 кв.ед.
Ответ: S=49 кв.ед.
Пример 10. Вычислить площадь треугольника с вершинами А(7;3;4), В(1;0;6) и С(4;5;-2).
Решение. находим векторы 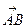 и
и  :
:
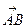 =
= 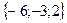
 =
= 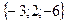
Площадь треугольника АВС равна половине площади параллелограмма построенного на векторах 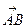 и
и  , поэтому находим векторное произведение этих векторов:
, поэтому находим векторное произведение этих векторов:
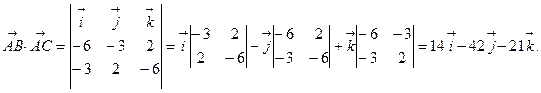
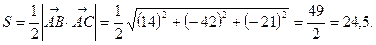
Ответ: S=24,5 кв.ед.
5.Смешанное произведение трех векторов.
10 Смешенным произведением векторов  и
и  , называется выражение вида
, называется выражение вида 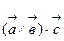 . Если векторы
. Если векторы  и
и  заданны своими координатами
заданны своими координатами  ,
,  ,
,  , то смешанное произведение определяется формулой:
, то смешанное произведение определяется формулой:
|

20 Свойства смешанного произведения:
1) 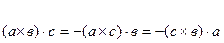
2) Если два из трёх данных векторов равны или параллельны, то их смешанное произведение равно 0.
3)  , поэтому смешанное произведение обозначается авс.
, поэтому смешанное произведение обозначается авс.
30 Объём параллелепипеда, построенного на векторах  и
и  :
: 
|

(+ при правой тройке, - при левой)
Объём пирамиды построенной на векторах 
 :
:
|

40 Если 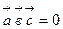 , то векторы
, то векторы 
 лежат в одной плоскости, т.е. компланарны. При этом, между
лежат в одной плоскости, т.е. компланарны. При этом, между  и
и  существует линейная зависимость вида
существует линейная зависимость вида 
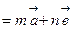 .
.
Пример 11. Найти смешанное произведение векторов 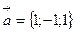 ,
, 

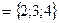 .
.
Решение. По формуле (15), находим:
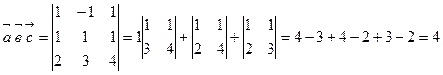 .
.
Ответ: 4.
Пример 12. Найти объём треугольной пирамиды с вершинами А(0;0;1), В(2;3;5), C(6;2;3) и D(3;7;2).
Решение. Найдём векторы  и
и 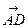 , совпадающие с рёбрами пирамиды, сходящимися в вершине А:
, совпадающие с рёбрами пирамиды, сходящимися в вершине А:

Найдём смешанное произведение этих векторов:

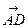 =
= 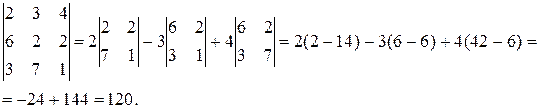
Так как объём пирамиды равен 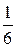 объёма параллелепипеда построенного на векторах
объёма параллелепипеда построенного на векторах  , то
, то  .
.
Ответ: 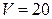 куб. ед.
куб. ед.
Пример 13. Даны радиус вектора трёх последовательных вершин параллелограмма ABCD:  Определить радиус вектора четвёртой вершины.
Определить радиус вектора четвёртой вершины.
Решение. 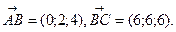 Пусть
Пусть
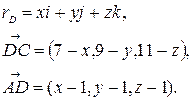
Так как 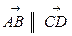 , то
, то  и так как
и так как 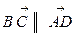 , то
, то  .
.
Решая систему

Получим x=7, y=7, z=7.
Ответ. 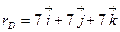 .
.
Пример 14. Установить, компланарны ли векторы 
 , если
, если 
Решение. Найдём смешанное произведение:

 =
= 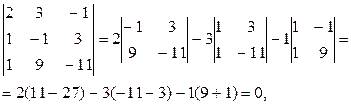
следовательно, векторы 
 компланарны.
компланарны.
Контрольные вопросы.
1.Векторы. Линейные операции над векторами.
2.Базис. Разложение вектора по базису.
3.Скалярные произведения.
4.Векторные произведения.
5.Смешанное произведение двух векторов.
Задания.
1. Проверить векторные тождества
1)  , 2)
, 2) 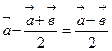 .
.
2. В равнобедренной трапеции ОАСВ угол ВОА=600 , ОВ=ВС=СА=2, М и N- середины сторон ВС и АС. Выразить векторы 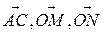 и
и  , через
, через 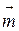 и
и  , где
, где 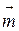 и
и  единичные векторы направлений
единичные векторы направлений 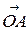 и
и 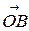 .
.
4. Вектор 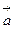 составляет с координатными осями ох и оу углы 600 и
составляет с координатными осями ох и оу углы 600 и  соответственно. Вычислить его координаты при условии
соответственно. Вычислить его координаты при условии 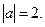
5. Даны точки А(2;2;0) и В(0;-2;5). Построить вектор 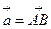 и определить его длину и направление.
и определить его длину и направление.
6. Даны векторы 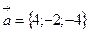 ,
, 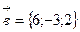 . Вычислить:
. Вычислить:
а)  , б)
, б) 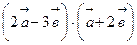 , в)
, в) 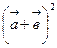 , г)
, г)  .
.
7. Определить при каком значении m векторы  и
и 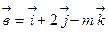 , взаимно перпендикулярны.
, взаимно перпендикулярны.
8. Даны точки А(3;3;-2), В(0;-3;-4), С(0;-3;0) и D(0;2;-4). Построить векторы  и найти
и найти 
9. Векторы 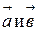 образуют угол
образуют угол  , зная что
, зная что 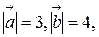 вычислить:
вычислить:
1)  , 2)
, 2) 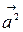 3)
3) 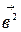 4)
4) 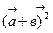 5)
5)  .
.
11.Векторы  составляют угол
составляют угол 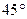 . Найти площадь треугольника построенного на векторах
. Найти площадь треугольника построенного на векторах  , если
, если 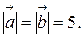
12.Даны векторы  . Найдите
. Найдите  и
и  . 13.Даны векторы
. 13.Даны векторы 
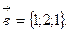 Найти координаты векторного произведения
Найти координаты векторного произведения 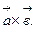
14.Вычислить площадь параллелограмма построенного на векторах  и
и  если
если  ,
, 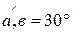
15.Вычислить площадь параллелограмма, построенного на векторах:  ,
, 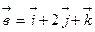 .
. 
16. Найти смешанное произведение векторов: a=i-j+k, в=i+j+k, c=2i+3j+4k.
17. Показать, что векторы: a=7i-3j+2k, в=3i-7j+8k, c=i-j-k - компланарны.
3) Вычислить объём треугольной пирамиды с вершинами А(0;0;1), В(2;3;5), С(6;2;3) и D(3;7;2). Найти длину высоты пирамиды, опущенной на грань BCD.
Занятие 5.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 3839; Нарушение авторских прав?; Мы поможем в написании вашей работы!