Решение системы линейных уравнений методом Гаусса

Пусть дана система m -линейных уравнений с n -неизвестными

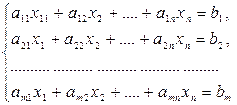
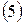
Решение системы линейных уравнений методом Гаусса заключается в последовательном исключении неизвестных и приведении данной системы уравнений к ступенчатому виду с помощью элементарных преобразований.

Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу даннойсистемы.

Рассмотрим расширенную матрицу даннойсистемы

.

.

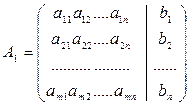Данную матрицу можно привести к ступенчатому виду при помощи следующих элементарных преобразований.

Процесс нахождения коэффициентов ступенчатой системы называется прямым ходом, а процесс нахождения неизвестных обратным ходом.

Пример 7. Решить данную систему методом Гаусса

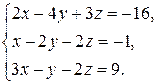
Решение. Напишем соответствующую расширенную матрицу .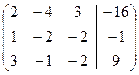

Введем 5-й, так называемый контрольный столбец:

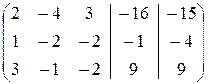
Контрольный столбец, каждый элемент которого равен сумме элементов соответствующей строки, вводим для проверки правильности преобразований. При линейных преобразованиях элементов матрицы такому же преобразованию должны подвергнутся элементы контрольного столбца, при этом каждый элемент контрольного столбца остается равным сумме всех других элементов соответствующей строки преобразованной матрицы. Переход от одной матрицы к другой будем записывать с помощью знака эквивалентности.

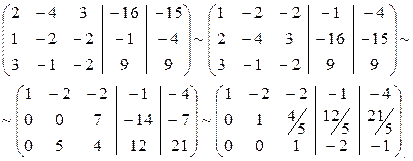
Этот процесс называется прямым ходом. Далее используя обратный ход, получим:

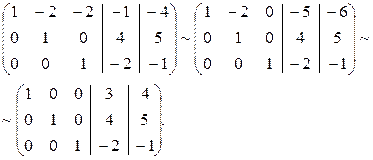
Итак получили: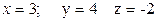

Ответ: .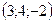

Контрольные вопросы

1. Матрицы

2. Обратная матрица

3. Матричный способ решения линейных уравнений.

4. Ранг матрицы.

5.Теорема Кронекера – Капелли

6. Исследование системы линейных уравнений.

7. Решение системы линейных уравнений методом Гаусса.

Задания.

1.Найти ранг матрицы

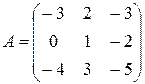
2. Решить системы матричным способом и методом Гаусса.

, , ,

,

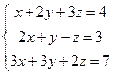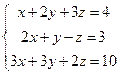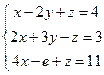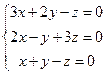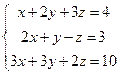
3.Решить матричные уравнения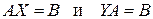

1) ;

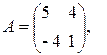
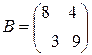2) ;

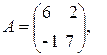
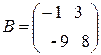3) .

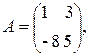
Дата добавления: 2014-12-16