
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение прямой
|
|
|
|
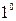 .Найдем уравнение прямой проходящей через точку
.Найдем уравнение прямой проходящей через точку 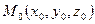 и параллельной вектору
и параллельной вектору 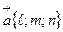 . Пусть
. Пусть  - произвольная точка прямой, тогда
- произвольная точка прямой, тогда 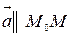 и по условию параллельности векторов:
и по условию параллельности векторов:
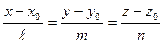 (8)
(8)
Уравнение (8)- называется каноническим и является искомым уравнением прямой. Вектор 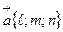 - называется направляющим вектором прямой.
- называется направляющим вектором прямой.
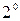 . Параметрическое уравнение прямой:
. Параметрическое уравнение прямой:
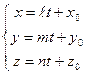 (9)
(9)
 .Уравнение прямой, проходящей через две точки
.Уравнение прямой, проходящей через две точки  :
:
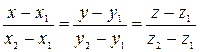 (10)
(10)
 . Общее уравнение прямой:
. Общее уравнение прямой:
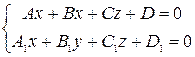 (11)
(11)
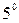 . Угол между прямыми. Угол между прямыми, заданными их каноническими уравнениями:
. Угол между прямыми. Угол между прямыми, заданными их каноническими уравнениями:  и
и  определяется по формуле
определяется по формуле
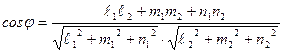 (12)
(12)
Условие параллельности двух прямых:
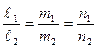 (13)
(13)
Условие перпендикулярности двух прямых:
 (14)
(14)
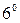 Углом между прямой и плоскостью называется любой из двух смежных углов, образованной прямой и ее проекцией на плоскость. Угол между прямой
Углом между прямой и плоскостью называется любой из двух смежных углов, образованной прямой и ее проекцией на плоскость. Угол между прямой 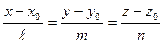 и плоскостью
и плоскостью 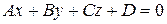 определяется по формуле
определяется по формуле
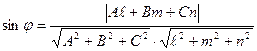 ; (15)
; (15)
Условие параллельности прямой и плоскости
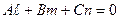 (16);
(16);
Условие перпендикулярности прямой и плоскости
 (17).
(17).
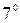 .Точка пересечения прямой и плоскости. Написав параметрическое уравнение прямой
.Точка пересечения прямой и плоскости. Написав параметрическое уравнение прямой 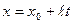 ,
, 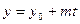 ,
, 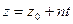 , и подставив ее в уравнение плоскости
, и подставив ее в уравнение плоскости  , получим некоторое значение
, получим некоторое значение 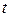 . Подставив найденное значение
. Подставив найденное значение 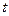 в уравнение прямой, находим искомую точку пересечения
в уравнение прямой, находим искомую точку пересечения  прямой с плоскостью.
прямой с плоскостью.
Пример 4. Составить уравнение прямой, проходящей через две данные точки  и
и 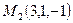 .
.
Решение. Воспользуемся формулой (10) получим: 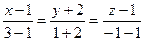 или
или 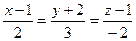 .
.
Пример 5. Найти расстояние между параллельными прямыми
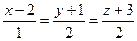 и
и 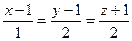 .
.
Решение. Точка 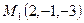 - точка первой прямой,
- точка первой прямой, 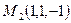 - точка второй прямой.
- точка второй прямой. 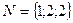 - направляющий вектор.
- направляющий вектор.
 , где
, где 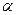 - угол между векторами
- угол между векторами  и N.
и N.
 ,
,  .
.
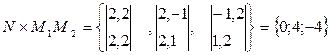 .
.
 .
.
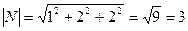 и
и 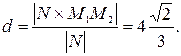
Ответ: 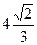 .
.
Пример 6. Для пирамиды с вершинами в точках:  ,
, 
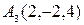
 найти
найти
а) длину ребра 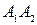
б) угол между ребрами 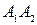 и
и 
в) уравнение плоскости 
г) площадь грани 
д) угол между ребром  и плоскостью
и плоскостью 
е) уравнение высоты, опущенной из точки 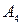 на грань
на грань 
ж) объем пирамиды 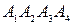
Решение. а) Длина ребра 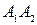
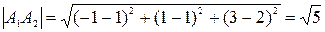 .
.
б) Угол между ребрами 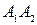 и
и  .
.
Обозначим через 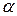 - угол между ребрами
- угол между ребрами 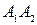 и
и  . Тогда, если угол между векторами
. Тогда, если угол между векторами 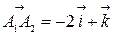 и
и 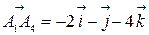 острый, то
острый, то 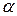 равен этому углу, если же угол между этими векторами тупой, то
равен этому углу, если же угол между этими векторами тупой, то 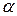 равен этому углу минус
равен этому углу минус 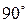 . Так как
. Так как
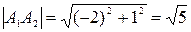 ,
,
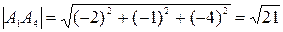 ,
,
 , то
, то
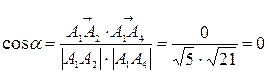 .
.
Отсюда, угол между векторами 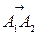 и
и 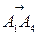 равен
равен 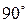 . Следовательно,
. Следовательно, 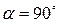 .
.
в) Уравнение плоскости  . Уравнение плоскости, проходящей через три точки, вычисляется по формуле
. Уравнение плоскости, проходящей через три точки, вычисляется по формуле

где 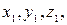

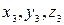 -соответственно координаты этих точек.
-соответственно координаты этих точек.
Таким образом,
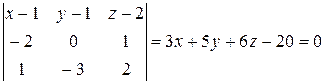 ,
,
 - уравнение плоскости
- уравнение плоскости  .
.
г) Площадь грани  .
.
Так как 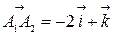 и
и 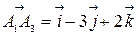
 , то
, то
 .
.
Отсюда 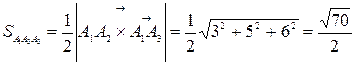 - площадь грани
- площадь грани  .
.
д) Угол между ребром  и плоскостью
и плоскостью  .
.
Угол 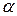 между ребром
между ребром  и плоскостью
и плоскостью  равен
равен 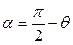 , где
, где
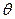 -угол между вектором
-угол между вектором 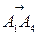 и нормалью к плоскости
и нормалью к плоскости  , т.е.
, т.е. 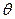 -угол между векторами
-угол между векторами 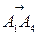 и
и  и
и 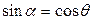 .
.
Так как 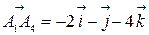 , то
, то 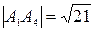 ,
,
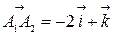 ,
, 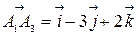 ,
, 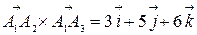 , то
, то  .
.
Следовательно, 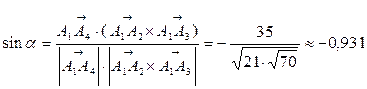 и
и
 .
.
е) Уравнение высоты, опущенной из точки 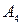 на грань
на грань  .
.
Пусть M – произвольная точка прямой, перпендикулярной плоскости грани  и проходящей через точку
и проходящей через точку 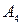 .
.
Тогда скалярные произведения 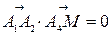 и
и 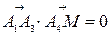 .Так как
.Так как 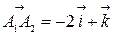 ,
, 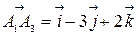 и
и 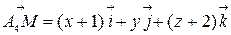 , то
, то 
Следовательно,
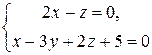
-уравнение искомой прямой.
Или 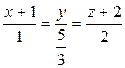 - каноническое уравнение искомой прямой.
- каноническое уравнение искомой прямой.
ж) Объем пирамиды 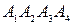 .
.
Так как 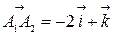 ,
, 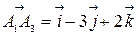 ,
, 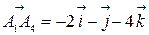 , то
, то
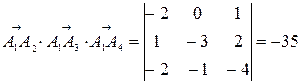 ;
;
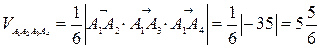 - объем пирамиды
- объем пирамиды 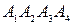 .
.
Контрольные вопросы.
1. Уравнение плоскости.
2. Угол между плоскостями.
3. Расстояние от точки до плоскости.
4. Уравнение прямой.
5. Угол между прямыми.
6. Прямая и плоскость
Задания.
1. Найти расстояние точки 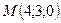 от плоскости проходящей через точки
от плоскости проходящей через точки 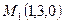 ,
,  ,
,  .
.
2. Найти плоскость, проходящую через точку 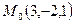 параллельно плоскости
параллельно плоскости 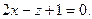 Найти угол между плоскостями
Найти угол между плоскостями  и
и 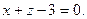
3. Составить параметрическое уравнение прямой проходящей через
точку  параллельно вектору
параллельно вектору 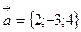 .
.
4. Составить каноническое уравнение прямой, проходящие через
две данные точки 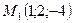 и
и 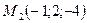 .
.
5. Написать уравнение плоскости, проходящей через
прямую 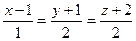 и перпендикулярной плоскости
и перпендикулярной плоскости  .
.
6.Для пирамиды с вершинами в точках: 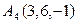 ,
, 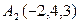
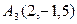
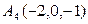 найти
найти
а) длину ребра 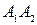
б) угол между ребрами 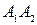 и
и 
в) уравнение плоскости 
г) площадь грани 
д) угол между ребром  и плоскостью
и плоскостью 
е) уравнение высоты, опущенной из точки 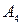 на грань
на грань 
ж) объем пирамиды 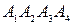
Занятие 6
Кривые второго порядка.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 550; Нарушение авторских прав?; Мы поможем в написании вашей работы!