Окружность. Окружность- это множество точек плоскости, равноудаленных от данной точки (центра)

Окружность- это множество точек плоскости, равноудаленных от данной точки (центра). Уравнение окружности с центром в точке 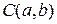и радиусом равным :

Если раскрыть скобки в левой части уравнения (1) то получится уравнение вида

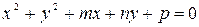
Пример 1. Написать уравнение окружности с центром 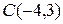и радиусом .

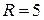Решение. Уравнение окружности с центром в точке 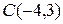и радиусом 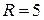есть:

.

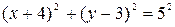1.Эллипс.

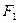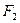Эллипсом называется геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек и , называемых фокусами, есть величина постоянная 2а. Т.е., если 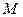- произвольная точка эллипса, то по определению эллипса имеем: 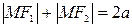. Числа 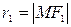, 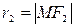называются фокальными радиусами точки .

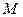Расстояние между фокусам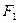и и 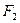обозначим через 2с. Примем за ось абсцисс, прямую соединяющую фокусы, выбрав на ней положительное направление от 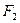к 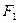; начало координат возьмём в середине отрезка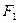 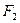. Тогда координаты точек 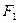и 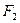будут соответственно: 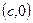и .

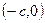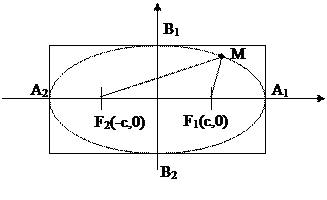Каноническое уравнение эллипса:

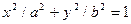(1)

где 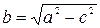, 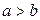. Числа 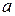и называются полуосями эллипса.

Вершины эллипса имеют следующие координаты , , , .

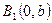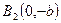Из уравнения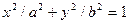

следует, что 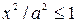или Аналогично, Следовательно, эллипс расположен внутри прямоугольника со сторонами, равными 2а и 2b, с центром в начале координат. Если а = b (с = 0), уравнение примет вид: х² + у² = а² и определяет окружность.

Отношение 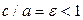называется эксцентриситетом эллипса. Величина эксцентриситета влияет на форму эллип­са. Так, при очень малом 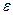а и b почти равны и эллипс напо­минает окружность. Если же величина 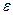близка к еди­нице, то эллипс имеет сильно вытянутую форму.

Пример2. Написать каноническое уравнение эллипса, если известно, что расстояние между фокусами равно 8,а малая полуось =3.

Решение. Расстояние между фокусами 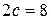, следовательно, .Так как 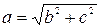,то .Следовательно, каноническое уравнение данного эллипса есть .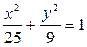

2. Гипербола.

Гиперболой называется геометрическое место точек, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная. Обозначим эту постоянную через 2а, а- расстояние между фокусами гиперболы. Пусть 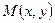- произвольная точка гиперболы.

По определению гиперболы имеем:

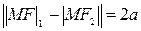
Числа 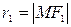, 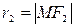называются фокальными радиусами точки .

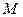Каноническое уравнение гиперболы:

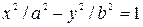(2)

где 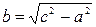,Число а- называется действительной, а число 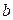- мнимой полуосями гиперболы.

Ось симметрии на которой находятся фокусы, называется фокальной осью, точка пересечения осей симмет­рии - центром гиперболы;

Отношение 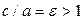называется эксцентриситетом гиперболы. Для любой гиперболы величина эксцентриситета опре­деляет форму гиперболы.

Замечание 1. у= (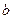 /а) х и у = - ( 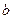/ а)х - асимп­тоты гиперболы. Если а = 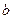, то такая гипербола на­зывается равносторонней.

Замечание 2. Если мнимая ось гиперболы равна 2а и расположена на оси Оx, а действительная ось равна 2 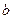и расположена на оси Оy, то уравнение такой гиперболы имеет вид:

y/а 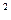- x²/ 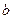² = 1 (3).

Гиперболы (2) и (3) называются сопряженными гиперболами.

Пример3. Гипербола проходит через точку (6,-2 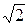) и имеет мнимую полуось =2.Написать ее уравнение и найти расстояние точки от фокусов.

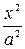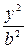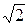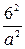Решение. Общий вид уравнения гиперболы есть: + =1. Гипербола проходит через точку (6,-2 ) и имеет мнимую полуось =2, следовательно, =3, a = 2 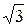.Следовательно, 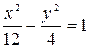-уравнение искомой гиперболы. .

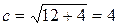и 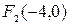-фокусы данной гиперболы. ,

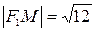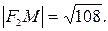
3. Парабола.

Парабола есть геометрическое место точек, равностоящих от данной точки, называемой фокусом, и данной прямой называемой директрисой.

Выберем систему координат таким

образом: за ось Оx примем прямую

проходящую через фокус .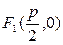

Пусть 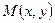- произвольная точка

лежащая на параболе. Пусть точка

N – основание перпендикуляра

опущенного из М на директрису.

По определению параболы .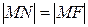

Каноническое уравнение параболы:

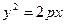. (3)

Уравнение директрисы записывается в виде: .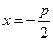

Точка (0.0) – точка пересечения параболы с осью симметрии и называется вершиной параболы.

Пример4. Написать уравнение параболы симметричной относительно оси ОХ и проходящей через точки (0,0) и (2,-4).

Решение. Уравнение параболы симметричной относительно оси ОХ и проходящей через начало координат есть 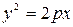.Точка (2,-4)-лежит на параболе, следовательно,(-4) 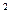= 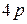, 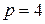и уравнение параболы имеет вид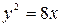

Контрольные вопросы.

1.Эллипс.

2. Гипербола.

3. Парабола.

Задания.

1.Написать уравнение окружности с центром 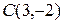и радиусом 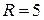. Лежат ли на этой окружности точки , , .

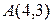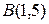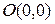2.Построить эллипс 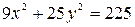. Найти: 1)полуоси, 2)координаты фокусов,3) эксцентриситет.

3.Построить гиперболу 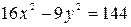. Найти: 1)действительную и мнимую полуоси, 2)координаты фокусов, 3) эксцентриситет, 4) уравнения асимптот.

4.Написать уравнение множества точек, одинаково удаленных от точки 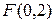и от прямой . Найти точки пересечения этой кривой с осями координат и построить ее.

Дата добавления: 2014-12-16