Основы комбинаторики

Тема 4. Теория вероятностей

Тема 3. Интеграл

Функция F(х) называется первообразной для функции f(х), если F^I(х) = f(х). Всякая непрерывная функция f(х) имеет бесконечное множество первообразных функций, которые отличаются друг от друга на постоянную. Неопределенным интегралом от функции f(х) называется совокупность всех ее первообразных.

Обозначают: 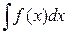= F(x)+с

Свойства неопределенного интеграла.

1. 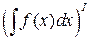= f(x) или d 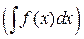= f(x) dx

2. F(x)+c или

3.

т.е. постоянный множитель можно выносить за знак интеграла.

4. 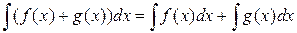, т.е. неопределенный интеграл от алгебраической суммы равен сумме интегралов.

Таблица основных интегралов

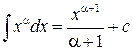1. (α≠-1)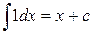
2.	3.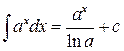
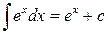
4.	5.
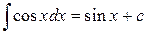
6.	7.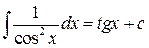
8.
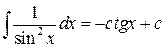
9.
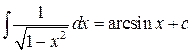
10.
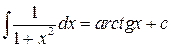
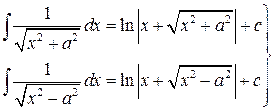
11. (формула «длинного» логарифма)
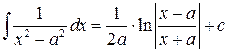
12. (формула «высокого» логарифма)

Найти интеграл:

Воспользуемся свойствами 3 и 4:

а)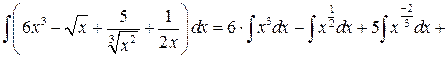

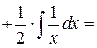воспользуемся табличными интервалами 1и 2:

Факториалом целого положительного числа n (обозначается n!) называется произведение 1·2·3·...·n = n! По определению 0!=1.

Основной закон комбинаторики. Пусть нужно произвести k действий, причем первое действие можно произвести n₁ способами, второе – n₂способами,... k-ое – n_k способами. Тогда все действия можно произвести n₁ · n₂ ·... · n_k способами.

Перестановкой из n элементов называется набор из n элементов, расположенных в определенном порядке. Число всех перестановок из n элементов равно: Р_n = n!

Размещением из n элементов по k элементов называется набор из к элементов, выбранных из данных n элементов в определенном порядке, т.е. два различных размещения отличаются либо составом элементов, либо (при одинаковом составе) порядком элементов.

Число всех размещений из n элементов по к элементов равно:

A_n^k =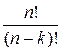

Сочетанием из n элементов по k элементов называется набор из k элементов, выбранных из данных n элементов в произвольном порядке, т.е. два различных сочетания отличаются только составом элементов.

Число всех сочетаний из n элементов по к элементов равно:

С_n^k =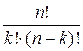

Основное свойство сочетаний: С_n^k = С_n^n-k

Дата добавления: 2014-12-16