Свойства систем

Системы и задачи их анализа

Понятие «система» не имеет, а по мнению некоторых авторов, и не может иметь исчерпывающего и однозначного определения. Это связано с первичностью, аксиоматическим характером понятия, поскольку понятие «системность» очень часто носит субъективный характер и оценивается через другие понятия, которые также являются первичными.

Блез Паскаль писал: «Я считаю, что познать части без знания целого так же невозможно, как познать целое без знания его частей».

Теория систем изучает общие проблемы связи целого и его частей. В более узком понимании это вопросы, связанные с решением следующих проблем:

- определение содержания проблем;

- назначение и (или) определение целей при принятии решений;

- поиск путей решения проблем;

- проектирование и (или) построение систем для достижения целей и т.д.

Так что же будет пониматься под термином «система»? Достаточно устоявшейся является мысль, что «система» («S») обладает минимум четырьмя свойствами:

1) Целостность и членимость

Целостность означает, что система воспринимается окружающей средой как единый элемент этой среды. Членимость означает, что в системе можно выделить некоторые элементы, совокупность которых вместе с их взаимодействием и образует систему. При этом совокупность элементов обладает качественно новыми свойствами, которые позволяют рассматривать их как элемент более сложной системы. Новое качество, эмерджентность, - это то, что определяет «лицо» системы, идентифицирует ее целостность, и поэтому оно первично для системы.

2) Интегративные качества

Свойства, обеспечивающие целостность, которые есть у системы, но нет у элементов, составляющих систему, называются интегративным качеством (ИК), они определяют эмерджентность. Существенно, что ИК не может быть выявлено сколь угодно глубоким изучением свойств элементов. Например, команда (бригада) может выполнить задачи, которые члены команды (бригады) по отдельности выполнить не в состоянии.

3) Связи (отношения)

Система, как правило, взаимодействует с другими системами (F_i, i=1,2,…), которые для нее являются внешней средой, связь осуществляется между некоторыми (или всеми) элементами, принадлежащими данной системе, и элементами других систем (см. рис. 1.1). Другие системы – это внешняя среда для системы S.

Если взаимодействие системы S с внешней средой не рассматривается (в теоретических исследованиях, например), тогда система называется закрытой или автономной. Множество переменных (координат), через которые система S взаимодействует с внешней средой, часто разделяют на подмножества входных X={x_i, i=1,2…} и выходных Y={y_j; j=1,2…} координат системы.

В реальном мире один и тот же элемент может входить в разные системы. Взаимодействие систем носит разноплановый характер, поэтому существенным вопросом является определение границ системы и выделение переменных Х,Y. Причем значение имеют только связи, определяющие интегративное качество, т.е. «имидж» системы.

Связь подсистем количественно задается множеством характеристик связей В={b_i, i=1,2,…}, к числу которых относится физическое наполнение (энергетическая, информационная, вещественная, механическая связь и т.д.), а также мощностью, направленностью и т.д.

S

F₁

F₂

х₁

х₂

х₃

х₄

у₂

у₁

границы системы S

границы системы F₁

границы системы F₂

Рис. 1.1 - Графическое представление системы и среды

Формально связь может быть представлена отображением b:Х® 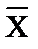при условии, что метрики множеств Х и 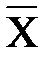связаны функцией f(b):

.

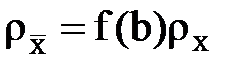Метрика (мера, расстояние)– это способ измерения расстояния между элементами множеств а,b,сÎХ.

Метрика должна удовлетворять некоторым определяющим свойствам:

а) r ≥ 0 при любых а,b,c;

б) r(a,b) = 0 тогда и только тогда, когда a = b (аксиома идентичности);

в) r(a,b) = r(b,a) (аксиома симметричности);

г) r(a,b) £ r(а,с) + r(с,b) (аксиома треугольника).

Пара (Х,r_Х) называется метрическим пространством.

Примеры метрик:

а) r(а,b) = |a - b|;

б) r₂(a,b) = 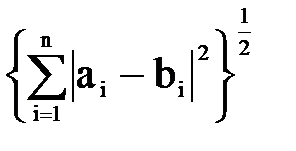- евклидова метрика в евклидовом пространстве Rⁿ,

в) r_¥(а,b) = 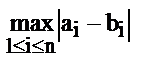- чебышевская метрика;

г) r_К(a,b) = 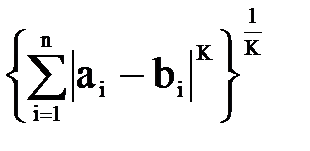- метрика Гельдера, К – целое.

В общем случае – отношения бывают: унарные (самого с собой); бинарные (между двумя элементами); тернарные (между тремя элементами); вообще, - n-арные.

4) Организация

Введем в рассмотрение понятие «состояние» элемента или системы.

Количество состояний (мощность множества состояний) может быть конечно, счетно (количество состояний измеряется дискретно, но их число бесконечно); мощности континуум (состояния изменяются непрерывно и число их бесконечно и несчетно).

Состояния можно описать через переменные состояния. Если переменные – дискретные, то количество состояний может быть либо конечным, либо счетным. Если переменные – аналоговые (непрерывные), тогда - мощности континуум.

Минимальное количество переменных, через которые может быть задано состояние, называется фазовым пространством. Изменение состояния системы отображается в фазовом пространстве фазовой траекторией.

Уравнение состояния системы:

Y = F(X, Z), (1.1)

где Z – переменные состояния (вектор аналоговых или дискретных величин),

Х – входные переменные, Y – выходные переменные системы.

Одной из наиболее часто используемых характеристик организации является энтропия (поворот, превращение – греч.).

Энтропия систем

Степень организации элементов в системе связывается с изменением (снижением) энтропии системы по сравнению с суммарной энтропией элементов. Понятие энтропии введено Больцманом для термодинамических систем:

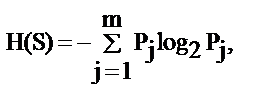(1.2)

где 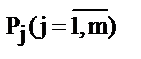- вероятность j-го состояния (в теории информации – события); m - возможное число состояний (событий).

Например, два элемента А и В могут каждый принимать два равновероятных состояния: «0»и «1». Вероятность каждого состояния:

Р₁(А) = Р₂(А) = Р₁(В) = Р₂(В) = 0,5.

Для одного элемента энтропия составит

Н(А) = Н(В) = -0,5 log₂0,5 - 0,5log₂0,5 = 1.

Энтропия двух элементов:

Н(А) + Н(В) = 1 + 1 = 2. ¨

Допустим, что система S элементов А и В может принимать три состояния: «-1», «0», «1» с вероятностями Р₁(S) = Р₃(S) = 0,2; Р₂ = 0,6.

Тогда

Н(S) = -2^.0,2^.log₂0,2 - 0,6^.log₂0,6 = -0,4×(-2,32) - 0,6×(-0,737) = 1,37.

Энтропия системы S меньше суммы энтропий элементов А и В на

DН = Н(А) + Н(В) - Н(S) = 2 - 1,37 = 0,63. ¨

Для расчета изменения энтропии системы через вероятности состояний очень часто используется метод Колмогорова.

Допустим, дана структурная схема (граф) состояний подсистемы S (см. рис. 1.2). Исходным состоянием системы с равной степенью вероятности может быть одно из четырех состояний, т.е.

l₂₁

l₃₂

l₁₄

l₂₄

l₄₃

Рис. 1.2

.

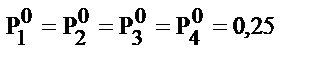Будем считать, что интенсивности переходов l₂₁, l₃₂, l₄₃, l₁₄, l₂₄ заданы. Тогда можно показать, что скорости изменения вероятности нахождения системы в i-м состоянии определяются как 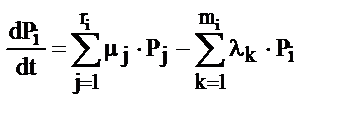, (1.3)

где 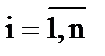; n – число узлов графа (количество состояний);

m_j 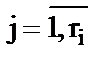- интенсивности переходов по дугам, входящим в i-й узел;

r_i – число дуг, входящих в i-й узел;

l_k 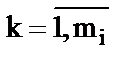- интенсивности переходов по дугам, исходящим из i-го узла;

m_i – число дуг, выходящих из i-го узла;

P_i и P_j – вероятности нахождения системы в i-м и j-м состояниях

соответственно.

Заметим, что

.

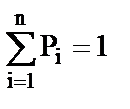Установившееся значение вероятности нахождения системы в i-м состоянии определяется из условия

.

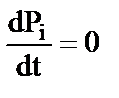Тогда для системы с n состояниями имеем систему из (n + 1) уравнений с n неизвестными:

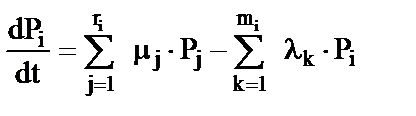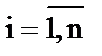; . (1.4)

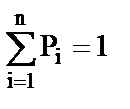
Одно из уравнений (1.4) можно отбросить, так как оно может быть получено из (n - 1) оставшихся.

Пример. Примем l₂₁ = 0,1, l₃₂ = 0,2, l₄₃ = 0,3, l₁₄ = 0,4, l₂₄ = 0,5. Тогда получаем:

l₁₄^.Р₄ - l₂₁^.Р₁ = 0

l₂₁^.Р₁ + l₂₄^.Р₄ - l₃₂^.Р₂ = 0

l₃₂^.Р₂ - l₄₃^.Р₃ = 0

l₄₃^.Р₃ – (l₁₄ + l₂₄)^.Р₄ = 0

Р₁ + Р₂ + Р₃ + Р₄ = 1.

Из системы отбросим второе уравнение и получим:

- 0,1^.Р₁ + 0^.Р₂ + 0^.Р₃ + 0^.Р₄ = 0

0^.Р₁ + 0,2^.Р₂ – 0,3^.Р₃ + 0^.Р₄ = 0

0^.Р₁ + 0^.Р₂ + 0,3^.Р₃ – 0,9^.Р₄ = 0

1^.Р₁ + 1^.Р₂ + 1^.Р₃ + 1^.Р₄ = 1.

Решение полученной системы: Р₁ = 0,32, Р₂ = 0,36, Р₃ = 0,24, Р₄ = 0,08.

Расчет энтропий ведется по формуле

.

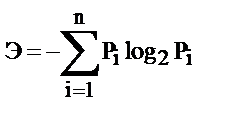Для исходного состояния

Э₀ = -4 ^. 0,25 ^. log₂0,25 = 2,

для конечного состояния

Э_к = -(0,32 ^. log₂0,32 + 0,36 ^. log₂0,36 + 0,24 ^. log₂0,24 + 0,08 ^. log₂0,08) = 1,835.

То есть, изменение энтропии составляет

DЭ = Э₀ – Э_к = 2 – 1,835 = 0,165. ¨

Существуют два основных подхода к расчету энтропий систем и ценности информации.

Первый подход основан на декомпозиции исходной задачи на этапы вычисления вероятностей апостериорной и априорной вероятности элементарных событий.

Методика расчета включает:

- декомпозицию исходной задачи на последовательность таких элементарных событий, априорная вероятность которых известна, а апостериорная может быть легко рассчитана;

- расчет энтропий (или ценности информации) каждого элементарного события;

- вычисление изменения энтропии исходного состояния по отношению к конечному (или ценности информации) путем суммирования изменений энтропий элементарных этапов (переходов, событий).

Данный подход позволяет избежать вычисление вероятности сложных событий.

Второй подход основывается на использовании условных вероятностей событий. Последние иногда рассчитать довольно сложно.

Таким образом, энтропия выступает в качестве меры хаоса, беспорядка и ее снижение означает увеличение организации.

Для информационных систем степень организации очень часто зависит от количества информации, которая может быть использована для управления.

1.2. Количество информации

В теории информации количество информации часто измеряют в битах (binary digital), где бит определяется как ценность I информации об исходе двух равновероятных событий. Например, эта информация о том, что сейчас день, а не ночь.

Вероятность каждого из событий

Р(Д) = 0,5; Р(Н) = 0,5;

I = log₂ 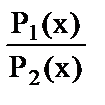, (1.5)

где Р₁(х) – апостериорная вероятность; Р₂(х) – априорная вероятность.

Для примера:

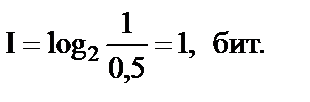
Кроме битов (термин ввел Тьюки) используются

«нат»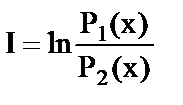

и

«дит» .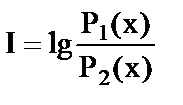

1.3. Классификация систем

Существует достаточно большое число классификационных признаков (свойств) систем, в частности:

- открытость – замкнутость (отсутствие связи с внешней средой);

- детерминированность (определенность) – стохастичность (случайность);

- простота – сложность;

-наличие цели – отсутствие цели;

- субстанциональные признаки (по этим признакам выделяют: естественные, концептуальные, искусственные системы);

- наличие направленности связей и характер связей: не направленные, обратные, линейные, нелинейные;

- наличие или отсутствие иерархии элементов в системе;

- эволюционирующие – не эволюционирующие (жесткие, не адаптируемые) системы;

- непрерывные – дискретные;

- по физическому наполнению: вещественные, энергетические, информационные и т.д.;

- по мощности связей: коэффициенты связи, интенсивности, чувствительности, коэффициенты корреляции и т.д.;

- по роли связи: ограничивающая, координирующая, положительная, отрицательная.

Для характеристики свойств систем выделяют факторы:

- системосоздающие;

- системоразрущающие;

- системозначимые (свойства, характеризующие интегративное качество, в том числе вне системы);

- системоопределяющие (свойства определяют интегративное качество системы) и др.

По признаку «сложность» выделяются два типа систем (простые - сложные).

Существует несколько аспектов, по которым система может классифицироваться как простая или сложная.

Достаточно общее с практической точки зрения определение сложной системы: это такая система, анализ и прогноз изменения состояния которой невозможен с заданной точностью за заданное время.

Для искусственных систем, к которым относится подавляющее большинство систем, создаваемых человеком, выделяют три основных уровня формулирования цели:

1) цель не очень ясна (целенаправленные системы);

2) цель ясна и намечены пути ее достижения (целеустремленные системы);

3) цель определена и формализована на уровне математической постановки, есть алгоритм достижения цели (алгоритмические системы).

Реальные постановки проблем могут представлять собой промежуточные варианты перечисленных случаев.

2. Элементы теории множеств

Наиболее общие формальные описания элементов и систем опираются на язык теории множеств. Рассмотрим некоторые элементы этой теории.

2.1. Основные понятия и термины

Множество – совокупность элементов, объединенных по какому-либо признаку.

Через «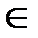» обозначается отношение принадлежности, то есть «х 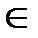А» означает, что х принадлежит множеству А. Если х не является элементом А, то пишется «х 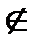А».

Множества А и В считаются равными, если они состоят из одних и тех же элементов: А = В. В противном случае А ≠ В.

Элементами множества могут быть любые объективные и субъективные понятия, объединяемые в соответствии с некоторым законом, правилом, признаком и т.д.

Множества могут содержать подмножества, например, если В - подмножество А, то оно записывается через отношение включения «В 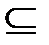А», то есть каждый элемент А является элементом В (но не наоборот, см. рис. 2.1).

Рис. 2.1

Если В 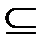А и А ≠ В, то В является собственным подмножеством А, т.е. В 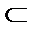А.

Множество, не содержащее элементов, называется пустым, например, В = Æ.

Семейство всех подмножеств множества А обозначается как Р(А).

Множества, элементами которого являются множества, обычно называют классом.

Задание множества можно осуществлять следующим образом:

1) перечислением А:= {a₁, a₂, …, a_n};

2) характеристическим предикатом (правилом):

А:= {x | P(x)},

например, элементами А являются все значения х такие, что sin(x) ³ 0.

3) порождающей процедурой:

А:= {x | x:= f},

например, А:= {n | for n = 1 to 9 do yield}.

Мощность множества А обозначается как .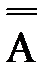

Мощностью множества А называется класс всех множеств, эквивалентных А. Эквивалентность (~), в отличие от равенства – это возможность установить взаимно однозначное соответствие между элементами множеств А и В: А ~ В.

Используются следующие основные градации мощности:

а) n–конечные множества - это мощность множеств из набора любых n элементов; множество конечно;

б) если элементов бесконечное количество, но их можно перечислить (например, множество чисел), мощность такого количества обозначают через χ₀. Оно называется счетным.

в) если множество эквивалентно множеству всех натуральных чисел, его мощность обозначается через С и оно называется континуальным (мощность континуума). Множество не счетно.

Мощности произвольных множеств называются кардинальными числами.

Очевидно, что С «больше» χ₀, а χ₀ «больше» n.

Возникает ряд вопросов: может ли мощность быть больше С? Например, какова мощность множества комплексных чисел? Как оценить эту мощность?

Введем в рассмотрение так называемое прямое (декартово) произведение множеств А и В:

М = А × В:= {(a, b) | a Î A, b Î B}.

Это множество упорядоченных пар элементов множеств А и В.

Если множество действительных чисел R имеет мощность С, множество мнимых чисел I также имеет мощность С. Тогда кажется, что 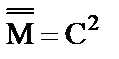. Однако можно показать, что .

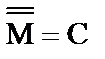Для ответа на подобные вопросы приведем свойства мощности:

n₁ + n₂ = n₁ + n₂, χ₀ + C = C, χ₀ ×χ₀ = χ₀,

n + χ₀ = χ₀, C + C = C, χ₀×C = C,

χ₀ + χ₀ = χ₀, n₁×n₂ = n₁×n₂, C×C = C.

Бинарным отношением между множествами А и В называется любое подмножество R Î A × В. Например, если А = В – множества четных действительных чисел от 0 до 8, тогда А × В – это множество пар четных чисел: 00, 02, 04, … 88.

2.2. Операции над множествами

1) Объединение (сумма, дизъюнкция)

Х = А È В:= {x | x Î A v x Î B}

«v» = «или» (см. рис. 2.2, а)

Х

А

б)

Х

А

В

в)

Х

А

В

г)

В

В

Х

А

а)

Рис. 2.2

2) Пересечение (произведение, конъюнкция)

Х = А Ç В:= {x | x Î A & x Î B}

«&» = «и» (см. рис. 2.2, б).

3) Разность (см. рис. 2.2, в)

Х = А \ В:= {x | x Î A & x Ï B}.

4) Симметрическая разность (см. рис. 2.2, г)

Х = (А \ В) È (В \ А) = А Δ В:= {x | x Î A & x Ï B, x Î В & x Ï А }.

5) Дополнение

.

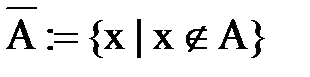Элементы всех множеств можно считать элементами некоторого универсального множества U – универсума, которыйиграет роль единицы. Тогда разность U \ A называется дополнением множества А и часто обозначается (-А) или (А).

2.3. Свойства операций над множествами

1) Идемпотентность: А È А = А, А Ç А = А.

2) Коммутативность: А È В = В È А, А Ç В = В Ç А.

3) Ассоциативность: А È (В È С) = (А È В) È С,

А Ç (В Ç С) = (А Ç В) Ç С.

4) Дистрибутивность: А È (В Ç С) = (А È В) Ç (А È С),

А Ç (В È С) = (А Ç В) È (А Ç С).

5) Поглощение: (А Ç В) È А = А, (А È В) Ç А = А.

6) Свойства нуля: А Ç Æ = Æ, А È Æ = А.

7) Свойства единицы: А Ç U = A, А È U = U.

8) Инволютивность: .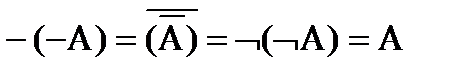

9) Законы де Моргана: , .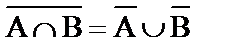

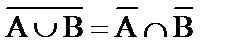10) .

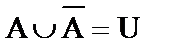
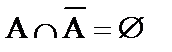11) .

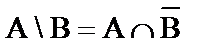12) Рефлексивность: А Í А.

13) Транзитивность: если А Í В и В Í С, то А Í С.

Алгебраическая операция определена на А, если можно указать закон, по которому любой паре (a, b) из А´А ставится в соответствие третий элемент, принадлежащий этому же множеству.

c = a + b – сложение, с = a×b – умножение, c = a°b – в общем случае.

Основные свойства операций: коммутативность и ассоциативность.

Операция – это всегда отношение, но не наоборот.

Множество К называется кольцом, если в нем определены операции сложения и умножения, обе ассоциативны и дистрибутивны, причем сложение коммутативно и обладает обратной операцией.

Множество К называется линейным или векторным пространством, если для элементов (векторов) из К определены операции сложения и умножения на число Р и выполняются аксиомы:

1) Каждой паре векторов (х, у) отвечает вектор (х + у) и называется суммой, причем х + у = у + х (коммутативность) и х + (у + z) = (х + у) + z (ассоциативность).

Существует единственный нулевой вектор О такой, что х + О = х, "х.

Существует вектор (-х) такой, что х + (-х) = О.

2) Каждой паре (a, х), где a - число, а х – вектор, отвечает вектор aх, причем:

a (b х) = (a b) х, 1×х = х.

3) a×(х + у) = a×х + a×у, (a + b)×х = a×х + b×х.

2.4. Алгебры

Множества и функции на них – это два типа объектов, на которых в конечном счете строится любая математическая теория.

Если аргументы функции f пробегают множество М и она принимает значения из того же множества, то f – это алгебраическая операция на М.

Итак, алгебра – это множество М вместе с набором операций на нем. Обозначается алгебра как двойка (М, S), где S:={j₁, j₂, …, j_n} – набор (множество) операций, сигнатура алгебры, а М – носитель алгебры.

Группой называется множество, если:

1) выполняется условие наличия одной ассоциативной операции;

2) в группе есть элемент «е», удовлетворяющий условию a^.e = e^.a = a, он называется «единицей»;

3) для каждого элемента а существует единственный элемент (а^-1) такой, что

a^.a^-1 = e, (a^-1)^.a = e.

Если, кроме того, для "a, b ÎG имеет место коммутативность a^.b = b^.a, то группа называется коммутативной или абелевой.

Дата добавления: 2014-12-16