Этап 3. Оценка согласованности приоритетов

Оценивается согласованность локальных приоритетов, т.е. правильности заполнения матриц парных сравнений. Заметим, что данный этап может выполняться сразу после заполнения матриц. В качестве оценки используются индекс согласованности (ИС) и отношение согласованности (ОС):

,

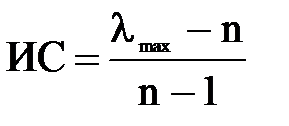где n – число сравниваемых элементов, l_max - максимальное собственное значение матрицы суждений (Ц, Кр1, Кр2…), l_max ³ n:

.

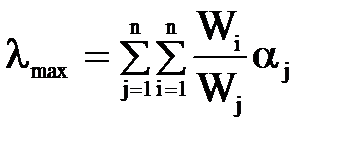ОС = ИС / СС,

где СС – случайная согласованность, определяемая по табл. 5.5.

Должно быть ОС £ 0,1…0,2, иначе следует пересмотреть матрицу суждений.

Таблица 5.5

n
СС	0,58	0,9	1,12	1,24	1,32	1,41	1,41	1,49

Группа математических методов решения сложных экспертиз

Как было видно в методе анализа иерархий, синтез приоритетов более высокого уровня в отношении вариантов самого низкого уровня проводится по соотношению

Ц_(1´m) = a_(1´n)хВ_(n´m),

где В – матрица приоритетов нижнего уровня по отношению к приоритетам верхнего уровня; a – приоритеты высшего уровня (критериев); m – число вариантов нижнего уровня; n – количество критериев.

Эта идея реализуется в методе решающих матриц.

Если начать с задания матрицы gⁿ предпочтений для альтернатив (нижний), (n -й уровень) по отношению к элементам (n-1) -о уровня, матрица А^n-1, то получим матрицу-строку A^n-2, учитывающую приоритеты двух нижних уровней. Продолжая процедуру формирования матриц приоритетов более высоких уровней

A^n-2 = gⁿ A^n-1

и умножения их на матрицы нижних уровней, получим для матрицы цели

Ц⁰ =^.gⁿ А^h-1.А^n-2…^.А¹.

В отличие от метода анализа иерархий назначение приоритетов на каждом уровне проводится многокритериальным, а не парным сравнением, что требует большей информированности эксперта.

Метод дерева целей еще менее формализован и ограничен, чем предыдущий.

Существует несколько типовых схем координации целей подсистем по уровням для сложных систем принятия решений.

Методы АИ и РМ по виду взаимодействия элементов соседних уровней относятся к так называемым ромбовидным иерархическим структурам. Для ромбовидной структуры характерно наличие зависимостей целей (i + 1) уровня от одних и тех же элементов i-го уровня (см. рис. 5.5).

Ц⁰

Ц¹

Ц²

Рис. 5.5

Метод дерева целей, как следует из его названия, не может использоваться для задач подобного вида, что является большим ограничением метода. В то же время очень большая выразительность и простота метода, являющегося методом когнитивной структуризации для большого круга практических задач, сделали его достаточно употребительным (рис. 5.6).

Ц⁰

Ц¹

Ц²

Рис. 5.6

Идея расчета глобальных приоритетов в методе дерева целей реализуется в несколько этапов:

1) строится граф (когнитивная карта), отражающий взаимодействие целевых функций между элементами различных уровней.

2) для каждой связи назначаются и нормируются веса элементов нижнего уровня для целей верхнего уровня.

3) вес (приоритет) альтернатив рассчитывается как произведение весов от альтернативы к вершине.

5.7. Семиотические методы

Семиотические методы базируются на моделях семиотического типа и относятся к области интересов Теории и методов искусственного интеллекта.

Помимо перечисленных моделей семиотического типа, используются такие виды моделей, как нейронные сети, фреймы, предикатные системы и т.д. Рассмотрение этих методов выходит за рамки возможностей данного пособия.

5.8. Группа экспертных методов

Отличие экспертных методов от всех предыдущих заключается в том, что помимо формирования процедуры принятия решений при известных предпочтениях эксперта ставится задача формирования и оценки правильности экспертных весов. Известны следующие экспертные методы:

- метод анкетирования,

- метод дискуссии,

- метод интервьюирования, в частности, метод Дельфы (наиболее формализованный),

- метод сценариев,

- метод «мозгового штурма» и т.д.

Метод дискуссии заключается в обмене мнениями, но решение принимает ЛПР.

Метод «мозгового штурма»: собирается группа лиц из разных областей и каждый предлагает варианты решения данной проблемы, при этом критика запрещена. Может оказаться, что какое-нибудь «абсурдное» мнение окажется правильным.

Синетика – генерирование решений (альтернатив) на основе ассоциативного мышления. Метод аналогичен «мозговому штурму», но подбираются специалисты с ассоциативным характером мышления и обладающие психологической совместимостью. Обсуждение ведется в режиме свободной дискуссии.

Метод сценариев заключается в составлении некоторых деревьев, отражающих причинно-следственные связи между посылами и результатами. Обычно составляются три сценария: пессимистический (для наихудших условий), оптимистический и наиболее вероятный.

Анкетирование и интервьюирование относятся к наиболее субъективным методам принятия решений.

Рассмотрим идею метода Дельфы.

В основу метода Дельфы положены следующие положения:

1) ставящиеся вопросы допускают возможность численного оценивания вариантов;

2) ответ на вопрос обосновывается экспертом;

3) ответы должны базироваться на достаточном объеме информации, которая может быть слабо формализованной.

Обработка анкет состоит в том, что оценки экспертов разбиваются на квартили, т.е. на интервалы ответов, примерно равные четверти мнений от числа экспертов.

Квартиль – одна из числовых характеристик распределения вероятностей. Если взять некоторую случайную величину Х, мнения экспертов от 0 до 1 с функцией распределения F(Х) – вероятность соответствующего Х, то квартилью порядка Р называется число К такое, что F(К_р) < Р, F(К_р + e) ³ Р, e ® 0. То есть квартиль – это диапазон изменения переменной, соответствующий мнению каждой четверти экспертов. Медиана характеризует «среднее» мнение экспертов, крайние квартили – разброс мнений.

Например, мнение каждого эксперта Х Î [0, 1], тогда выделяется примерно четверть экспертов, которые утверждают, что величина Х Î [Х₁, Х₁⁺]. В результате опроса формируется плотность распределения мнений в виде ступенчатого графика или в идеале, при большом числе экспертов, непрерывной кривой.

1 этап. Формирование группы координаторов (штаба).

2 этап. Выбор группы экспертов, т.е. лиц, принимающих решения (ЛПР).

Выбор проводится на основе анкет для экспертов: вопросы анкеты формируются, исходя из целей координаторов. Например: 1) практический опыт решения аналогичных задач, 2) уровень образования, 3) возраст и т.д.

3 этап. Составляется вопросник (анкеты) по существу проблемы с указанием числовых критериев ответов. Это начало первого тура.

4 этап. Обработка ответов. Каждый эксперт отвечает на вопросы и обосновывает свое решение. Работа ведется анонимно. Мнения экспертов упорядочиваются по оси Х, и эксперты разбиваются на четыре группы. Мнения крайних групп экспертов озвучиваются (доводятся до всех экспертов) с обоснованиями.

5 этап. Выделение группы решений-претендентов на выход в следующий тур. Составление (коррекция) вопросников 2-го тура.

6 этап. Проводится 2-й тур аналогично первому. Далее 3-й тур и т.д. Обычно необходимы 3-4 тура. Критерий окончания процедуры – отсутствие изменений в мнениях экспертов. Существует два варианта:

1) найдено общее мнение, решение принято;

2) эксперты к единому мнению не пришли, требуются дополнительные исследования.

Близким к методу Дельфы является Дельфийское совещание. Отличие данного метода: обработка анкет не проводится анонимно, а мнение экспертов просто озвучивается.

5.9. Игровые методы принятия решений

Игровые методы принятия решений рассматривают вопросы принятия решений в условиях:

1) конфликтного взаимодействия элементов системы,

2) неопределенности,

3) сложности задачи принятия решений, вызванной многообъектностью системы.

Существует пять принципов конфликтного взаимодействия:

1) антагонизм,

2) бескоалиционное взаимодействие,

3) коалиционное взаимодействие,

4) кооперативное взаимодействие,

5) иерархическое взаимодействие с правом первого хода сверху.

Теория игр – математическая теория конфликтных ситуаций. Ее цель – дать инструмент для выработки разумного поведения участников конфликта.

Наиболее простой случай ситуаций, для которых имеется неопределенность – это случай конфликтных ситуаций, когда сталкиваются противоположные интересы двух или более групп. Выигрыш каждой стороны зависит от поведения соперника, а оно неизвестно.

Игра ведется по правилам, т.е. должны быть указаны права и обязанности участников. Игра может быть парной и множественной.

Каждый участник делает ходы, которые могут быть личные и случайные. Некоторые игры (часто азартные) не являются предметом теории игр. Если ходы число случайные, то это предмет для теории вероятности.

Если существуют правила вида «если ситуация А, то я поступлю В», значит принята стратегия игры. В зависимости от числа стратегий могут быть конечные и бесконечные игры.

Оптимальной называется стратегия, которая обеспечивает максимальный выигрыш. Если есть случайные ходы, то говорят о максимизации выигрыша в среднем.

Игра называется игрой с нулевой суммой, если алгебраическая сумма выигрыша всех участников равна нулю. Самая простая игра с нулевой суммой называется антагонистической (игра со строгим соперником). Теория таких игр наиболее развита и строга.

Рассмотрим игру G с игроками А и В. Будем считать, что «мы» - это А, а противник – В. Пусть у нас имеются m возможных стратегий А_i, а у противника – n стратегий B_j, то есть игра будет (m´n).

Обозначим выигрыш А через a_ij, где i - стратегия А, j – стратегия В. Предполагается, что для всех пар стратегий А_i и В_j выигрыш a_ij известен (а значит, проигрыш В также известен a_ij = - b_ij). Представим информацию в виде таблицы 5.6.

Таблица 5.6

	В1	В2	…	Вn
А1	a11	a12	…	a1n
А2	a21	a22	…	a2n
…	…	…	…	…
Аm	am1	am2	…	amn

Игра приведена к матричной форме. Обозначим эту матрицу как L = {a_ij}.

Если цифры в строках одинаковые – стратегии называются дублирующими. Можно упростить матрицу, если в ней имеются дублирующие и доминирующие стратегии как по строкам, так и по столбцам путем отбрасывания таких стратегий.

Рассмотрим пример G(4´5) (см. табл. 5.7). Если мы выберем максимально выигрышную стратегию А₃ (до 10), то противник выберет В₃ и выигрыш будет всего 1. Отсюда типичный принцип игры: минимальный выигрыш должен быть максимальным (принцип минимакса).

Добавим к табл. 5.7 столбец a_i и строку b_j, в которые выпишем минимальные выигрыши для столбца и максимальные для строки.

Таблица 5.7

	В1	В2	В3	В4	В5	ai
А1
А2
А3
А4
bj

Противник выбирает стратегию, где его проигрыш минимален. Таким образом, исходя из принципа осторожности мы будем выбирать А₄, а противник В₃.

Теперь предположим, что мы узнали о том, что противник выбрал В₃, тогда мы выбираем А₁ и получаем выигрыш 5. Но если противник узнал, что у нас А₁, он выберет В₄ и наш выигрыш будет 2. Мы и противник начали метаться. Это очень важно: минимаксные стратегии неустойчивы по отношению к информации о поведении другой стороны.

Иногда минимаксные стратегии дают устойчивое решение, когда a = b. В этом случае говорят, что совпадают верхняя и нижняя цена игры. Стратегии А_i и В_j, дающие на пересечении a = b, называются чистыми, а квадрат матрицы, соответствующий таким стратегиям – седловой точкой матрицы.

Можно показать, что решение игры сводится к задаче линейного программирования:

L_A = x₁ + x₂ + … + x_m ® min

при ограничениях вида

a₁₁^.x₁ + a₂₁^.x₂ + … + a_m1^.x_m ³ 1,

a₁₂^.x₁ + a₂₂^.x₂ + … + a_m2^.x_m ³ 1,

a_1n^.x₁ + a_2n^.x₂ + … + a_mn^.x_m ³ 1

при выборе стратегии А^*.

Выбор стратегии В аналогичен, но L_B ® max при выборе стратегии В^*.

Пара задач линейного программирования, по которой находится решение (А^*, В^*), называется двойственной. Показано, что минимум одной линейной функции соответствует максимуму другой.

Стабильно зависимое решение в зависимости от постановки задачи бывает:

1) скалярным Нэш-равновесием,

2) векторными равновесиями,

3) угрозы – контругрозы (УКУ),

4) векторно-оптимальное решение,

5) дележ по Шекли.

Для решения всех этих задач имеются соответствующие алгоритмы.

5.10. Имитационное моделирование

Имитационное моделирование (ИМ) имеет целью не только проверку решений, но и их генерирование на основе дуальной процедуры моделирования и разработки модели. Характерной особенностью ИМ является итеративный характер формирования модели объекта и модели принятия решений. ИМ позволяет решать следующие задачи:

1) проверку принимаемых решений,

2) формирование адекватных моделей объектов,

3) оптимизацию решений на управление,

4) техническую и психологическую подготовку операторов к решению сложных задач (задача разработки тренажеров-имитаторов).

Структура имитационной системы (ИС) состоит из модели объекта, модели вычисления показателей качества и эффективности (ПКиЭ), блока инициализации управления (ИУ), блока формирования интенсивности управления (ФИУ), блока интерфейса (MMI – Man-Machine Interface, человеко-машинный интерфейс).

модель вычисления ПКиЭ

блок ИУ

блок ФИУ

MMI

модель объекта

Х

Y

Рис. 5.7

На рис. 5.7 обозначены параметры: Х – возмущение (воздействие окружающей среды, может быть, модель внешней среды), Y – некоторое управляющее воздействие на объект управления.

Общая идеология использования и создания ИС состоит в том, что построение системы, выбор моделей, проведение экспериментов – это итерационный процесс. Модели элементов усложняются и уточняются на основе анализа чувствительности свойств (характеристик) системы к изменению характеристик (моделей) элементов.

Как правило, модели формируются в терминах «вход-выход» и изображаются на топологическом уровне в виде функциональных блоков, имеющих наборы входных и выходных координат. Такой подход используется в ряде программных пакетов имитационного моделирования: VisSim, СИАМ, DinSim, Simulink (MatLab) и др. Отличительной чертой этих пакетов является возможность для большинства задач избежать необходимости программирования стандартных для моделирования функций и процедур.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Дж. Ван Гиг. Прикладная общая теория систем.-М.: Мир. 1981. Кн.1 - 336с. Кн.2 - с.336-733.

2. Николаев В.И., Брук В.М. Системотехника: методы и приложения.- Л.:Машиностроение, 1985. -199с.

3. Диалектика и системный анализ.-М.:Наука, 1986. -336с.

4. Холл А.Д. Опыт методологии для системотехники.-М.:Сов. радио.1975.-448с.

5. Прангишвили И.В. Системный подход и общесистемные закономерности. –М.: СИНЕГ, 2000. -520 с.

6. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ: Учеб. пособие для вузов. - М.: Высшая школа, 1989.

7. Захаренко Н.Н., Минеева Н.В. Основы системного анализа. -М., 1992 - Ч. I.

8. Черняк Ю.И. Системный анализ в управлении экономикой. - М.: Экономика, 1975.

9. Варенник В.В., Шишкин А.В. Основы научных исследований. - М., 1990.

10. Моисеев Н.Н. Математические задачи системного анализа. - М.: Наука, 1981.

11. Черняк Ю.И. Анализ и синтез в экономике. - М.: Экономика, 1970.

12. Клиланд Д., Кинг В. Системный анализ и целевое управление. - М.: Сов. радио, 1974.

13. Оптнер С. Системный анализ для решения деловых и промышленных проблем. - М.: Сов. радио, 1969.

14. Саати Т., Кернс К. Принятие решений. Метод анализа иерархий.-М.: Радио и связь. 1993.-224 с.

15. Кусимов С.Т., Ильясов Б.Г., Исмагилова Л.А., Валеева Р.Г. Интеллектуальное управление производственными системами. –М.: Машиностроение, 2001. – 327 с.

16. Построение системного проекта с использованием IDEF-технологии: Учеб.-метод. пособие / Сост. О.В. Кирюшин. -Уфа: Изд-во УГНТУ, 2000. -32 с.

17. Рей У. Методы управления технологическими процессами.-М.:Мир, 1983.-368 с.

18. Васильев В.И. и др. Многоуровневое управление динамическими объектами. -М.: Наука, -309 с.

19. Вавилов А.А., Имаев Д.Х. Эволюционный синтез систем управления: Учеб. пособие.-Л.: ЛЭТИ, 1983.-80 с.

20. Веревкин А.П., Дадаян Л.Г. Анализ и синтез автоматических систем регулирования сложных объектов нефтепереработки и нефтехимии: Учеб. пособие.-Уфа: УНИ, 1989. -94 с.

21. Веревкин А.П., Динкель В.Г. Технические средства автоматизации химико-технологических процессов. Синтез логических устройств: Учеб. пособие.- Уфа: УНИ, 1989. -87 с.

Дата добавления: 2014-12-16