Пример 3.1

W₁

W₂

W₃

W₄

W₅

Рис. 3.2

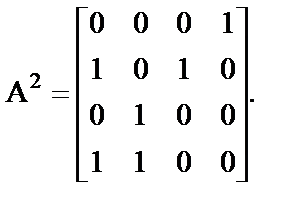
Как видно (см. рис. 3.2), через две (k = 2) смежные дуги можно попасть: из вершины 1 в вершину 4, из 2 в 1, из 2 в 3, из 3 в 4, из 4 в 1 и из 4 в 2. ¨

Таким образом, можно алгоритмически определить, существует ли путь из v_i в v_j длиной в k дуг. Очевидно, что если число узлов m, максимальная степень k, в которую нужно возвести А для определения самого длинного пути, равна (m – 1).

Матрица инцидентности – в общем случае прямоугольная матрица В = {b_ij}, 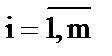, , где m – число вершин, n – число ребер. Для орграфов:

b_{ij =}

1, если i – начальная вершина ребра j

-1, если i – конечная вершина ребра j

0, если нет связи.

Для неориентированных:

b_{ij =}

1, если есть связь i-й вершины с j-м ребром

0, если нет связи.

№№ вершин

Для примера 3.1 матрица инцидентности имеет вид:

¨

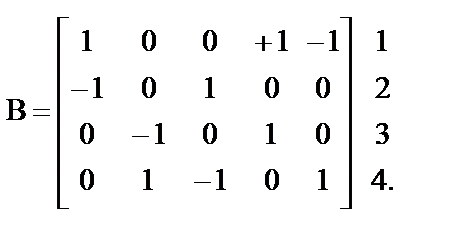
Матрица структуры связей С = {c_ij} устанавливает отношения между дугами:

С = В^Т×В,

С – симметрическая матрица размером n x n, т.е. С_nxn, для которой

c_{ij =}

2, если i = j или дуга r_i кратна дуге r_j

-2, если дуга r_i симметрична дуге r_j

1, если дуга r_i параллельно смежна дуге r_j

-1, если дуга r_i последовательно смежна дуге r_j

0, если дуга r_i не смежна дуге r_j.

r_i

r_j

r_i

r_i

r_i

r_j

r_j

r_j

r_i

r_j

кратные дуги

симметричные дуги

параллельно смежные дуги

последовательно смежные дуги

Рис. 3.3

Таким образом, матрица структуры связей содержит информацию о взаимной ориентации пар дуг графа.

Кроме этого, могут использоваться структурные матрицы, кодирующие отдельные свойства графов:

- наличие контуров (контур = замкнутый путь),

- наличие путей,

- отношения касания.

Касающимися называются пути, контуры или пути с контурами, если они содержат хотя бы один общий узел.

Сильносвязанным называется граф, в котором любой узел достижим из любого другого узла.

Достижимость – это существование пути из узла v_i в узел v_j. Например, на рис. 3.3 путь из узла 1 в узел 4 имеет вид:

узел 1 ® W₁ ® узел 2 ® W₂ ® узел 3 ® W₄ ® узел 4.

W₁

W₄

W₂

W₃

W₅

Рис. 3.4

Может оказаться, что не все узлы достижимы из остальных узлов. В этом случае может быть выделен подграф Г₁, т.е. совокупность, подмножество узлов, для которого условие сильной связности выполняется. Например, граф Г (см. рис. 3.4) не сильносвязный, т.к. в узел 1 из узлов 2, 3 и 4 нет путей. Сильносвязной компонентой Г₁ для графа Г состоит из узлов 2, 3 и 4 с соответствующими дугами W₂ – W₅.

Физический смысл сильной связности – наличие обратных связей (ОС) между всеми узлами или, другими словами, взаимозависимость (взаимовлияние) всех переменных в графе.

Важность понятия «сильная связность» вытекает из того, что практически все целенаправленные системы строятся на основе принципа обратной связи, когда информация о выходных величинах (координатах) некоторого объекта используется для формирования управляющего сигнала U этим объектом.

Структура простейшей системы управления описывается графом (см. рис. 3.5), где W₁ можно интерпретировать как модель объекта управления, а W₂ – модель управляющего устройства. Узлы 1 – управление U, 2 и 4 можно интерпретировать как выходную величину объекта у, 3 (ε) –ошибка регулирования, узел 5 – задание х (желаемое значение величины у).

W₁

U

х

у

ε

W₂

Рис. 3.5

4. Модели систем

4.1. Цели моделирования систем

Основными задачами моделирования является адекватное представление информации для достижения двух основных целей: во-первых, для анализа характеристик (свойств) систем и, во-вторых, для синтеза (разработки) систем, отвечающих заданным условиям. Имея в виду, что искусственные системы являются, в конечном счете, системами управления, можно сказать, что целью моделирования при анализе является оценка характеристик систем при различных уровнях представления информации об объекте, а при синтезе – разработка модели управляющей части системы (системы принятия решений).

Кроме основных целей моделирование может использоваться также для проверки работоспособности управляющего устройства в разных режимах работы (данный процесс моделирования называется тестированием), для улучшения качества процессов управления (системы управления с моделью), проверки решений параллельно с их генерированием (имитационное моделирование) и т.д.

4.2. Уровни моделирования

4.2.1. Классификация уровней моделирования

Существует достаточно большое количество классификационных признаков для моделей элементов и систем, однако, наиболее общим является объем информации, который несет в себе модель. Уровень определенности информации определяет границы, при которых модель и объект или модели разного вида сохраняют гомоморфизм (иногда говорят «гоморфизм»), т.е. могут рассматриваться как адекватные в смысле определенных критериев близости.

С указанной точки зрения выделим следующие уровни моделирования:

1) Концептуальный уровень, когда определяются границы системы (элемента), т.е. указываются векторы входных и выходных координат системы (элемента).

2) Топологический уровень, когда определены связи входных, выходных и внутренних переменных системы. Моделями данного уровня являются графы. Если, кроме того, указаны (хотя бы в общем виде, без задания структуры операторов) интенсивности связей, то моделями этого уровня являются сети.

3) Структурный уровень, когда определена структура операторов, описывающих взаимосвязь входных, выходных и внутренних переменных. Например, взаимосвязь может задаваться функциональными статическими соотношениями, операторами описания динамики (дифференциальные, интегральные уравнения, передаточные функции и т.д.), матричными преобразованиями и т.д.

4) Параметрический уровень, когда заданы параметры операторов связей, т.е. модель данного уровня полностью определена (в той степени, в которой определены параметры) и над ней могут проводится наиболее информативные эксперименты и делаться расчеты.

При использовании моделей различных уровней возникают вопросы:

1) Какие задачи позволяет решать модель того или иного уровня?

2) Для каких задач модель каждого уровня является информационно не избыточной?

Ответы на эти вопросы позволяют определить минимально допустимый уровень информации для решения тех или иных задач, что, в свою очередь, позволяет минимизировать затраты ресурсов на формирование баз данных и разработку методов анализа моделей.

4.2.2. Задачи анализа свойств систем, решаемые на концептуальном уровне

На концептуальном уровне могут решаться задачи декомпозиции (разбиения) на подсистемы и агрегации (объединения) подсистем в систему. Эти процедуры являются неотъемлемыми элементами анализа и синтеза сложных систем, в том числе, на основе системного подхода. Основа методов декомпозиции и агрегации – мнение экспертов, специалистов предметной области.

4.2.3. Задачи, решаемые на топологическом уровне

На моделях топологического уровня могут решаться следующие основные задачи:

1) определение общих характеристик и структурных свойств системы,

2) определение эквивалентных передач на графе (сети),

3) выделение подсистем в системе.

Рассмотрим пути решения некоторых задач.

I. Определение структурных свойств системы

Определяются следующие характеристики:

Степень централизации, которая оценивает тип структуры, к которому тяготеет данный граф. Известны несколько основных типов структур (см. рис. 4.1).

а) сетевая

б) скелетная

в) централистская

Рис. 4.1

Структуры сложных систем управления тяготеют к структурам иерархического типа (см. рис. 4.2), рыночных хозяйственных структур – к скелетному типу.

Рис. 4.2

Количественно неравномерность загрузки элементов графа характеризуют индексами центральности. Для ненаправленного графа:

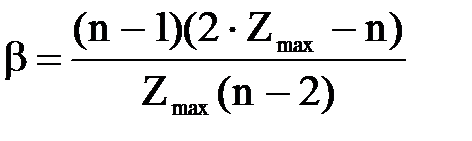, (4.1)

где

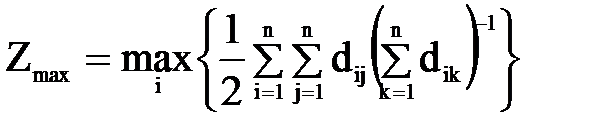, (4.2)

n – число вершин графа,

d_ij – длина минимального пути (при i = j длина d_ij = 0).

Для графа на рис. 4.1, а, когда все вершины инцидентны одному и тому же количеству ребер, b» 0. Для графа на рис. 4.1, в b» 1.

Для ориентированного графа индекс центральности

, (4.3)

где V(i) = v_i + vⁱ – суммарное число входящих и исходящих ребер i-й вершины, а .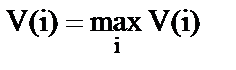

Диаметр структуры оценивается максимальным числом связей, разделяющих входные и выходные элементы графа:

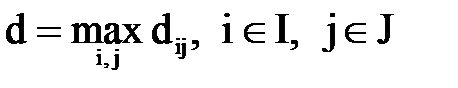, (4.4)

где I – множество вершин-истоков, J – множество вершин-стоков, d_ij - минимальный путь от i к j.

Связность – наименьшее число вершин, удаление которых приводит к несвязному графу.

Реберная связность – наименьшее число ребер, которое приводит к несвязному графу.

Известны и другие характеристики: сложность, наличие контуров, петель, сильносвязных компонент, отношения касания и т.д.

II. Определение эквивалентных передач

Требуется установить эквивалентный оператор, описывающий связь от i-го узла к j-му узлу с учетом всех связей графа.

Для сигнальных графов Мезоном получено следующее соотношение:

, (4.5)

где Δ – определитель графа:

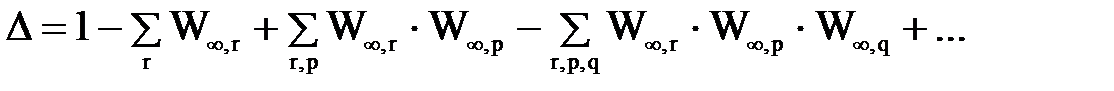(4.6)

W_¥,r (r = 1,2,…) - передаточный коэффициент r-го разомкнутого контура (определяется как произведение передач входящих в контур дуг),

W_¥,r^. W_¥,p (p,r = 1, 2, …, r ¹ p) – произведение «пар» передаточных коэффициентов некасающихся контуров, далее аналогично для «троек», «четверок» и т.д. некасающихся контуров;

P_k – передача k-го прямого пути, определяемая как произведение передаточных коэффициентов дуг, образующих путь;

Δ_k – минор k-го прямого пути (составляется аналогично определителю, но для подграфа, полученного из исходного графа при удалении узлов, принадлежащих k-му прямому пути).

III. Выделение подсистем в системе

Задача может решаться:

- формальными методами,

- концептуально (в этом случае концептуальное выделение должно подтверждаться на основе формальных процедур).

Формальные методы обычно базируются на анализе топологии (структуры системы), концептуальные – на функциональных характеристиках в тех или иных аспектах. Рассмотрим формальные методы выделения подсистем, базирующиеся на двух основных подходах:

а) подсистемами считаются несвязные сильные компоненты графа. Порядок выделения следующий:

- определяется множество всех сильносвязных компонентов;

- на полученном множестве выделяется подмножество пар, троек и т.д. сильносвязных компонентов, которые являются некасающимися.

б) подсистемами считаются сильносвязные компоненты, получающиеся при удалении дуг-мостов. Анализ графа обычно проводится в предположении, что число удаляемых дуг должно быть минимально. Вначале отыскиваются единичные дуги, удаление которых нарушает сильную связность графа, но сохраняет не менее двух сильных компонент. Если таких друг нет, ищутся пары дуг, удаление которых вызывает описанный эффект и т.д.

Концептуальные методы выделения подсистем базируются на неформальных признаках выделения подсистем. Например, для графа на рис. 4.3,а можно насчитать пять сильносвязных компонент (кроме самого графа), но концептуально подсистемами можно считать, например, подграфы, изображенные на рис. 4.3, б и в.

-R₁₁

W₁₁

W₃₁

W₂₄

-R₂₂

W₂₂

W₅₄

W₃₃

-R₃₃

а) граф S

-R₁₁

W₁₁

-R₂₂

W₂₂

W₅₄  

W₃₃

-R₃₃

б) подсистема S₁

в) подсистема S₂

Рис. 4.3

Проверку силы связности компонент можно осуществлять различными методами, в частности:

- с помощью матрицы Бристоля [17 ],

- метода Розенброка (метод проверки диагональной доминантности) [18 ],

- метода Вавилова-Имаева [19 ].

Рассмотрим последний метод подробнее на примере графа, изображенного на рис. 4.4. Предположим, что системы S₁ и S₂ не связаны, то есть организованы в систему S ошибочно. Определитель такой несвязной системы будет равен

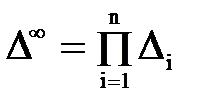, (4.7)

где n – число подсистем (в примере n = 2), Δ_i – определитель i-й подсистемы.

В примере

Δ₁ = 1 + W₁₁^.R₁₁, Δ₂ = 1 + W₂₂^.R₂₂, (4.8)

Δ_¥ = 1 + W₁₁^.R₁₁ + W₂₂^.R₂₂ + W₁₁^.R₁₁^.W₂₂^.R₂₂. (4.9)

-R₁₁

W₁₁

W₂₃

W₄₁

W₂₂

-R₂₂

S₁

S₂

S

Рис. 4.4

Определитель системы с учетом существующих связей:

Δ = 1 + W₁₁^.R₁₁ + W₂₂^.R₂₂ + W₁₁^.R₁₁^.W₂₂^.R₂₂ – W₂₃^.R₁₁^.W₄₁^.R₂₂. (4.10)

Можно видеть, что разность определителей

δΔ = Δ - Δ_¥ = – W₂₃^.R₁₁^.W₄₁^.R₂₂. (4.11)

Очевидно, что если

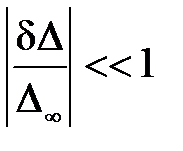, (4.12)

«добавкой» δΔ можно пренебречь и подсистемы S₁ и S₂ рассматривать как независимые. Модуль в (4.12) берется потому, что, во-первых, «добавка» δΔ может быть как со знаком «+», так и со знаком «-», во-вторых, значения δΔ, Δ и Δ_¥ - это не обязательно действительные числа. Операторы передач W_ij, K_kp (i, j, k, p – целые числа) могут быть произвольными объектами, в том числе комплексными числами и матрицами. Поэтому модуль может пониматься, по крайней мере, в трех смыслах:

- для действительных чисел – число без знака (со знаком «+»);

- для комплексных чисел p = α + j^.ω, где - мнимая единица:

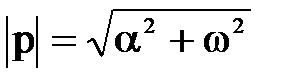; (4.13)

- для матриц – определитель матрицы.

4.2.4. Модели структурного уровня

Различают модели элементов в статике и в динамике.

Моделями статики являются функции вида

y = f(x),

где х и у соответственно входные и выходные координаты системы, которые не зависят от времени или их значения рассматриваются как установившиеся (t®¥).

f – функция, которая может задаваться аналитически, графически или алгоритмически.

Динамические модели и характеристики описываются линейными и нелинейными дифференциальными уравнениями, разностными уравнениями. уравнениями в частных производных, операторными уравнениями, передаточными функциями и др.

4.2.5. Модели параметрического уровня

Прежде, чем говорить о задании параметров, необходимо сказать, что параметры могут быть измерены в разных шкалах. Существует четыре уровня измерений:

1) шкала наименований (примеры: Иванов, Эверест,…);

2) шкала порядка – имеется признак, по которому производится сравнение, но не обязательно в виде числа (пример: холодно – тепло – горячо);

3) шкала интервалов – используются числа, характеризующие разности границ интервалов (пример: температура в гр. Цельсия или Фаренгейта);

4) шкала отношений.

Для шкал 3-го и 4-го уровней справедливы группы аксиом:

1) аксиомы тождественности

А = В (или А ¹ В),

если А = В, то В = А,

если А = В и В = С, то А = С;

2) аксиомы рангового порядка (для их выполнения требуется, чтобы выполнялось условие сравнимости и транзитивности; например, нельзя сравнивать бифштекс с книгой)

если А > B, то B < A,

если А > В и В > С, то А > С (то же для нестрогого порядка);

3) аксиомы аддитивности

если А = Р и В > 0, то А + В > Р,

А + В = В + А,

если А = Р и В = Q, то А + В = P + Q,

(А + В) + С = А + (В + С).

Кроме переменных, измеряемых действительными числами, существуют комплексные числа, задаваемые парой (а,в) действительных чисел, одно из которых (а) условно измеряет действительную, а второе (в) - мнимую составляющую.

Кроме того, существуют также переменные, измеряемые нечеткими, лингвистическими «числами», характеризуемые парой (х, m_х), где х нечеткая переменная, m_х - функция принадлежности к какому-либо множеству. С помощью таких переменных измеряют (оценивают) человеческие ощущения. Данные числа сложно отнести к какому-либо из вышеперечисленных типов и следует согласиться, что это особый тип чисел.

4.3. Классификация моделей систем

Одна из возможных классификаций моделей, используемых в процессе анализа и синтеза (создания) систем, представлена на рис. 4.5.

Среди моделей различного вида и назначения выделяются два принципиально различных типа:

-первый тип предназначен для описания характеристик (свойств) систем, т.е. для целей анализа;

-второй тип предназначен для принятия каких-либо решений с целью достижения целей.

В дальнейшем эти типы моделей будем условно обозначать как Мс – модели систем и Мт – модели требований. Рассмотренные выше примеры моделей, в основном, могут быть отнесены к типу Мс.

Модели

Качественные

Математические

Статистические

ЛМ

СС

ПС

Аппроксиматоры

Механистические модели

Вероятностные

Корреляционные

НЛМ

ДУ

ПФ

АМ

Рис. 4.5

Основными элементами моделей типа Мт являются:

- -цели и критерии, по которым осуществляется выбор решения;

- модели принятия решений: законы регулирования и управления, алгоритмы формирования управлений, схемы и процедуры принятия решений и т.д.

Все возможные варианты постановки задач построения целенаправленных систем являются бинарными отношениями (декартовым произведением) этих двух типов моделей

S = Мс ´ Мт.

Далее в п.п. 4.4 и 4.5 будут рассмотрены некоторые виды моделей типов Мс и Мт.

4.4. Модели систем типа Мс

Рассмотрим несколько видов классификационных признаков и соответствующие классы моделей, не претендуя на попытку обоснования их выбора. Заметим только, что сочетания различных классификационных признаков могут образовывать достаточно большое разнообразие практически выделяемых классов моделей.

Аппроксиматоры, называемые также в литературе «черными ящиками» (black box), «формальными моделями», являются разновидностью математических моделей, описывают функциональные связи между входами и выходами моделируемой системы без учета (при отсутствии) каких-либо знаний о топологии системы. Коэффициенты таких моделей могут не иметь какого-либо физического смысла, не соотносятся, например, с технологическими параметрами процессов. В этом заключается недостаток таких моделей. Однако, эти модели эффективны в случае невозможности или трудности построения строгих математических описаний поведения систем.

Распространенными примерами таких моделей являются нейронные сети (НС).

Механистические модели. Если знания о функционировании модели формализованы, то для описания таких моделей могут быть использованы механистические модели (ММ), к числу которых относят:

- алгебраические модели (АМ), представляющие собой системы алгебраических и трансцендентных уравнений,

- дифференциальные уравнения (ДУ) и системы ДУ,

- передаточные функции (ПФ),

- логические модели (ЛМ) и др.

Такие модели обычно получают путем анализа физических и химических основ моделируемых процессов. Результатом анализа является прямая или обратная модель процесса. Прямая модель отражает влияние входных координат процесса на выходные и может быть представлена в виде функции

Y = F(X),

где Х и Y - множества входных (в том числе управляющих) и выходных координат соответственно.

В ряде случаев необходимым является получение обратной модели вида

X = Q(Y_н),

где Y_н - множество наблюдаемых или измеряемых значений выходных координат процесса. В большинстве случаев построение обратных моделей является некорректной задачей, т.е. имеющей более одного решения или вообще его не имеющей.

Статистические модели являются технологией построения моделей путем описания свойств процесса через статистические переменные и соответствующие статистические оценки этих переменных. По своей сути эти модели содержат элемент неопределенности.

Модели, согласно этой технологии, строятся с использованием методов статистического анализа, теории игр, теории информации и т.п.

Разновидностями данных моделей являются вероятностные и корреляционные модели. Вероятностные модели используют плотности вероятности переменных процесса. При этом наиболее часто используются нормальный и экспоненциальный законы распределения. Использование таких моделей ограничено тем, что при числе переменных более двух требуется большое число экспериментов, возникают трудности, связанные с коррелируемостью параметров.

Динамические модели и характеристики описывают поведение систем в динамике, т.е. во времени.

Наиболее часто динамические модели представляются линейными и нелинейными дифференциальными уравнениями, разностными уравнениями в частных производных, операторными уравнениями, передаточными функциями и др.

Линейными называются элементы, для которых справедлив принцип суперпозиции:

L(х₁ + х₂) = L(х₁) + L(х₂),

где L - некоторый оператор.

Таким свойством обладают операторы суммирования, интегрирования, дифференцирования.

При исследовании динамических свойств систем может быть использованы прикладные математические методы операционного исчисления. Например, функционирование некоторой системы описывается ДУ вида

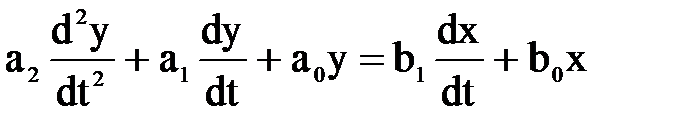, (4.14)

где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что

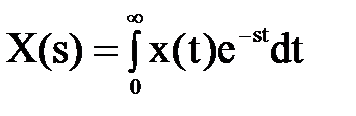и , (4.15)

то ДУ (4.14) при нулевых начальных условиях равносильно линейному алгебраическому уравнению

a₂ s² Y(s) + a₁ s Y(s) + a₀ Y(s) = b₁ X(s) + b₀ X(s).

Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (2.2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением.

Новые функции X(s) и Y(s) называются изображениями для x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s).

Переход от одной модели к другой заключается в замене знаков дифференциалов 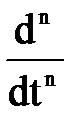на операторы sⁿ, знаков интегралов на множители 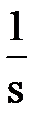, а самих x(t) и y(t) - изображениями X(s) и Y(s).

Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:

,

где f(t) - оригинал, F(jw) - изображение при s = jw, j - мнимая единица, w - частота.

Преобразование ДУ по Лапласу дает возможность ввести понятие передаточной функции, характеризующей динамические свойства системы.

Например, операторное уравнение

3s²Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s)

можно преобразовать, вынеся X(s) и Y(s) за скобки и поделив друг на друга:

Y(s)*(3s² + 4s + 1) = X(s)*(2s + 4),

.

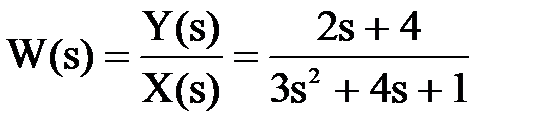Полученное выражение называется передаточной функцией.

Передаточная функция - это отношение изображения выходного воздействия Y(s) к изображению входного X(s) при нулевых начальных условиях:

.

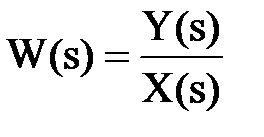Передаточная функция для линейных элементов часто является дробно-рациональной функцией комплексной переменной:

,

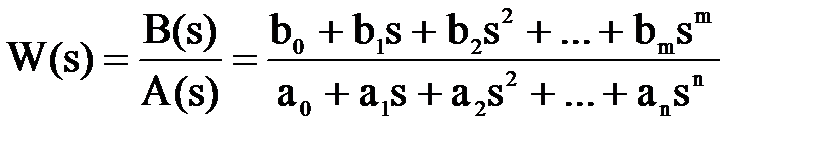где B(s) = b₀ + b₁s + b₂ s² + … + b_m s^m - полином числителя,

А(s) = a₀ + a₁s + a₂ s² + … + a_n sⁿ - полином знаменателя.

Если вместо s подставить выражение s = j^.w, получаем преобразование Фурье, которое характеризует связь между частотными характеристиками входных и выходных сигналов элемента. Частотные характеристики дают возможность анализировать описание системы с учетом динамики.

В последнее время более широко используется описание динамики систем методом пространства состояний.

Для описания динамики элементов систем используется в данном методе матричная запись ДУ:

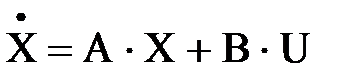, (4.16)

где А – матрица коэффициентов, U – матрица входов или управлений, Х – матрица пространства состояний:

Х = (х₁, х₂, … х_n)^Т.

В данном случае х_i называется переменной состояния или фазовой переменной («Т» – символ транспонирования).

Предположим, что динамические свойства объекта описываются ДУ вида

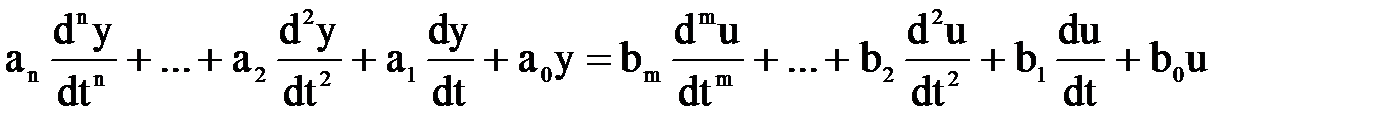, (4.17)

где a_i и b_i – коэффициенты, у – выходной сигнал, u – входной сигнал объекта.

Если ввести переменные состояния:

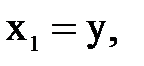
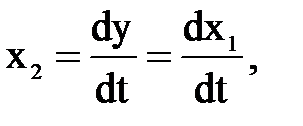
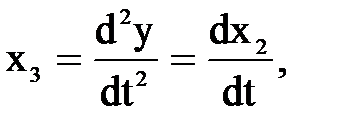и т.д.,

то левая часть ДУ (4.17) примет вид (после деления на (-а_n ):

.

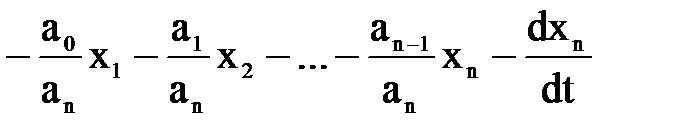Можно записать уравнение в матричном виде:

.

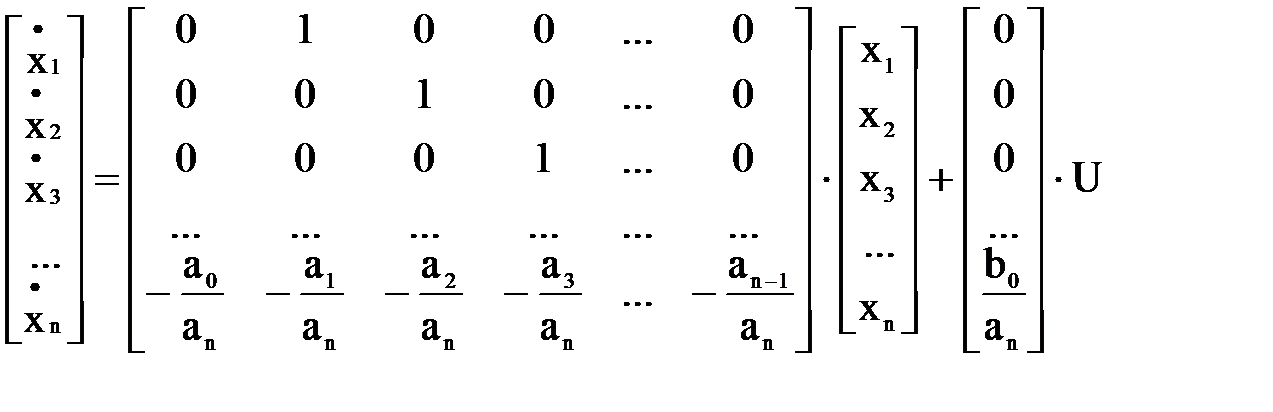Решением полученного матричного уравнения является матрица Х.

Для определения выходных параметров y_i уравнение (4.16) дополняется уравнением

Y = C^.X + D^.U,

где С (p´n) – матрица связей, D (p´q) – матрица обхода, p – число выходных параметров у_i, q – число входных параметров u_i.

Решение матричных уравнений для некоторых случаев может быть произведено аналитически, в частности, для однородного ДУ вида

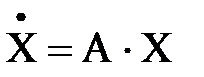. (4.18)

Прямое преобразование Лапласа для данного уравнения дает

s^.X(s) – X₀ = A^.X(s),

где Х₀ – матрица начальных условий, т.е. начальные условия по переменной у, по скорости ее изменения, ускорению и т.д. Отсюда получено

Х(s) = X₀^.[s^.E – A]^-1 = Ф(s)^.X_0,

где Е – единичная матрица, Ф(s) – изображение фундаментальной матрицы

Ф(s) = [s^.E – A]^-1.

Оригиналом фундаментальной матрицы является матричный экспоненциал

.

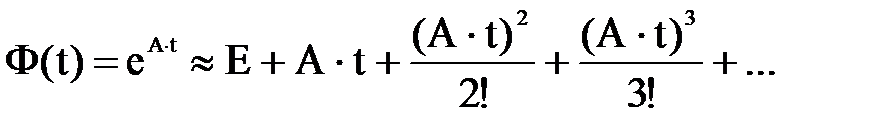Тогда решение ДУ (4.18) можно получить в виде ряда с шагом Dt по времени:

Х₀ – начальные условия,

Х(Dt) = Ф(Dt)^.Х₀,

Х(2^. Dt) = Ф(2^.Dt)^.Х(Dt) и т.д.

Дата добавления: 2014-12-16