Качественные модели

Существует множество примеров, когда природа процессов принятия решений или функционирования объекта не может быть описана в виде математических соотношений в виду наличия нечетких определений и лингвистических операций или ограничений на технологические параметры и т.д.

Решением этой проблемы является использование качественных моделей, которые наиболее часто представляются в терминах нечетких множеств.

4.5. Модели требований типа М_Т

Спектр моделей требований весьма широк, т.к. отражает уровень формализованности как целей и критериев, так и моделей принятия решений.

На одном конце этого спектра лежат модели требований для наиболее простых систем принятия решений – регуляторов или простейших видов управляющих устройств, используемых для формирования управлений в автоматических системах регулирования (АСР), а на другом – схемы экспертного, субъективного, характера.

4.5.1. По своей сути модели регуляторов являются моделями типа Мс механистического класса.

Если считать, что информацией является ошибка регулирования

е = х – у,

где х – желаемое значение регулируемого параметра, у – его текущее значение, то управляющее воздействие может формироваться, например, с использованием трех наиболее часто используемых законов:

П-закона регулирования (пропорциональный), для которого управляющее воздействие определяется как

U = K₁^.e,

где K₁ – коэффициент усиления регулятора;

И-закона (интегральный), для которого

;

Д-закона (дифференциальный), для которого

. ¨

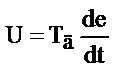Обычно используются сочетания перечисленных законов регулирования: ПИ- и ПИД-законы.

4.5.2. В более сложных случаях, когда требуется описывать процессы принятия решений с участием человека на тех или иных этапах, эти модели оказываются мало пригодными. Некоторые особенности моделей принятия решений с участием человека рассмотрим на примере оптимизационной задачи, когда решение принимается на основе процедуры оптимизации по множеству показателей или критериев - векторному критерию.

Заметим, что задача формирования управляющих переменных на основе процедуры оптимизации по одному (скалярному) критерию, также как и на основе стандартных законов регулирования, является полностью формализованной и относится к алгоритмическим методам принятия решений.

Векторный критерий состоит из набора (множества показателей), в числе которых могут быть показатели с разными направлениями шкалы полезности.

Направление шкалы полезности связывает категории «больше»-«меньше» с категориями «лучше»-«хуже».

Например, чем выше цена, тем хуже для покупателя, но чем выше качество товара, тем лучше для того же покупателя.

При оптимизации по скалярному критерию решение получается как наилучшее (с учетом ограничений), соответствующее минимуму или максимуму критерия в зависимости от направления шкалы полезности. Иное дело, если показателей несколько.

Рассмотрим задачу выбора решения для случая, когда имеется векторный критерий состоит из двух показателей:

.

Оба показателя имеют одинаковые шкалы полезности: чем меньше, тем лучше. Если для какого-либо показателя направление шкалы не совпадает с установленным, то для изменения направления шкалы полезности вводится показатель вида I’_I = 1 / I_i или I’₁ = - I₁ (I’_I – уровень «плохости»).

Рассмотрим задачу покупки товара наилучшего качества за наименьшие деньги (см. рис. 4.6). Ресурсом оптимизации (варьируемым параметром или параметрами q), от которых зависят значения показателей I₁ (q),I₂(q) будут варианты товара у разных продавцов.

Движение начнем с произвольного выбора товара, точка 0. Далее будем выбирать товар либо более дешевый и не худшего качества, либо более качественный, но не более дорогой товар.

При этом каждая последующая точка пути соответствует лучшему соотношению цены и качества. В конце концов, наступит момент (точка 3), когда описанную процедуру выполнить не удастся, т.е. одновременное улучшение по двум показателям будет невозможно.

I₁

I₂

I₁₀

I₂₀

O

M

Рис. 4.6

Точка 3 принадлежит множеству решений

М ={q^* | arg{J ® opt}}

– множеству Парето (множество компромиссов, переговорное множество). Это множество не улучшаемых в смысле векторного критерия решений, (в рассматриваемом случае opt = min). Существенно, что решение задачи оптимизации по векторному критерию носит принципиально множественный характер и для выбора наилучшего варианта нужен суперкритерий, который устанавливает приоритеты между показателями. Приоритеты, в конечном счете, устанавливает человек – лицо, принимающее решение (ЛПР).

Существует несколько методов получения решений из множества Парето:

1) метод сворачивания векторного критерия в глобальный скалярный,

2) метод последовательных уступок,

3) метод минимизации по частному критерию или показателю и ряд других.

Метод сворачивания векторного критерия

Сворачивание может производится по одной из следующих форм:

1) Аддитивный критерий

,

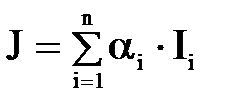где α_i – веса (весовые коэффициенты) показателей.

Если показатели имеют разные шкалы или размерности, то для облегчения выбора весов иногда эти показатели нормируют:

,

где 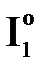- минимально (максимально) возможное значение показателя.

Веса также нормированы, т.е. .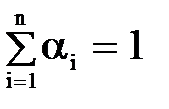

Физический смысл минимизации такого критерия – это минимизация общих потерь (применений, когда все показатели имеют одинаковый смысл).

2) Линейно-квадратичный критерий

.

Минимизация по такому критерию эквивалентна нахождению точки, ближайшей к началу координат (с учетом весов). Физический смысл - минимизация среднеквадратичных (статистических) потерь.

3) Минимаксный (Чебышёвский) критерий

.

Физический смысл – минимизация самой большой потери.

4) Модель справедливого компромисса

.

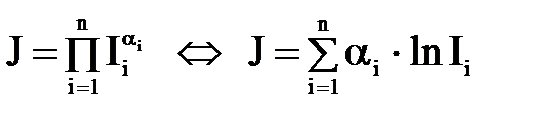Для случая n = 2 имеем α = α₁ = α₂ = 0,5 и решение

.

То есть относительные потери по одному критерию приводят к относительному выигрышу другого и наоборот.

Метод последовательных уступок

Метод требует большой определенности информации о приоритетах показателей (об их важности). Последовательность применения метода:

1 шаг. Все показатели должны быть расположены в порядке убывания приоритетов.

2 шаг. Отыскивается минимум старшего (наиболее важного) показателя и назначается уступка

I₁ £ I₁^* + DI₁.

3 шаг. В рамках назначенной уступки проводится минимизация очередного критерия и т.д.:

…

.

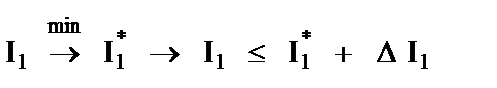
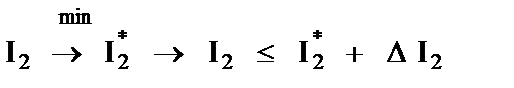
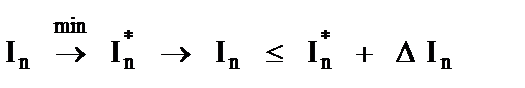Метод минимизации по частному критерию или показателю

Метод можно рассматривать как вариант предыдущего, если уступки по всем критериям, кроме наименее важного, известны.

Дата добавления: 2014-12-16