Шар и сфера

Шар

III уровень

3.1. Радиус основания конуса равен R, образующая наклонена к плоскости основания под углом a. В конусе через вершину под углом j к его высоте проведена плоскость. Найдите площадь полученного сечения.

3.2. Площади оснований усеченного конуса равны 81p см² и 225p см², образующая относится к высоте как 5: 4. Найдите площадь осевого сечения.

3.3. Диагонали осевого сечения усеченного конуса взаимно перпендикулярны. Площадь осевого сечения равна 324 см². Найдите площади оснований конуса, зная, что радиус одного основания на 2 см больше другого.

3.4. Дана трапеция ABCD, у которой AD = 15 см, BC = 9 см, AB = CD = 5 см. Трапеция вращается вокруг оси, проходящей через вершину A и перпендикулярно AD. Найдите площадь поверхности полученного тела вращения.

3.5. Прямая отсекает от сторон прямоугольного треугольника, угол между которыми 60°, отрезки, длины которых составляют четвертую часть длины гипотенузы, считая от вершины этого угла. Найдите отношение площади треугольника к площади поверхности тела, полученного при вращении этого треугольника вокруг прямой.

3.6. Конус лежит на плоскости и катится по ней, вращаясь вокруг своей неподвижной вершины. Высота конуса равна h, образующая – b. Найдите площадь поверхности, описываемой высотой конуса.

3.7. Два конуса имеют общее основание. В общем осевом сечении образующая одного из конусов перпендикулярна противолежащей образующей другого. Объем одного из них вдвое меньше объема другого. Найдите угол между образующей большего конуса и плоскостью оснований конусов.

3.8. Треугольник АВС, у которого АВ = 13 см, ВС = 20 см, АС = 21 см, вращается вокруг оси, которая проходит через вершину А перпендикулярно АС. Найдите объем полученного тела вращения.

3.9. Параллелограмм вращается вокруг оси, проходящей через вершину острого угла перпендикулярно большей диагонали. Найдите объем тела вращения, если стороны параллелограмма и его большая диагональ равны соответственно 15 см, 37 см и 44 см.

3.10. Образующая усеченного конуса, равная l, наклонена к плоскости основания под углом a. Отношение площадей оснований конуса равно 4. Найдите объем усеченного конуса.

Сферой называется множество всех точек пространства равноудаленных от данной точки.

Данная точка называется центром сферы. Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы. Хордой называется отрезок соединяющий две точки сферы. Диаметром называется хорда, проходящая через центр сферы (рис. 40).

Шаром называется геометрическое тело, ограниченное сферой. Центр, радиус, хорда и диаметр сферы называются соответственно центром, радиусом, хордой и диаметром шара (рис.40).

Шар можно рассматривать, как тело, полученное при вращении полукруга вокруг оси, содержащей диаметр полукруга.

Сферой также называется поверхность шара.

Рис. 40

Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью к сфере (шару). Общая точка называется точкой касания сферы (шара) и плоскости.

Теорема. Для того чтобы плоскость была касательной к сфере (шару) необходимо и достаточно, чтобы эта плоскость была перпендикулярна к радиусу сферы (шара), проведенному в точку касания.

Для шара верны формулы:

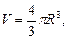
где R – радиус шара;

S – площадь поверхности шара (площадь сферы);

V – объем шара.

Дата добавления: 2014-12-16