I уровень. Многогранники и тела вращения

Многогранники и тела вращения

Цилиндр называется описанным около призмы, если окружности оснований цилиндра описаны около оснований призмы, а боковые ребра призмы являются образующими цилиндра. Призма соответственно называется вписанной в цилиндр.

Теорема. Для того чтобы около призмы можно было описать цилиндр, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.

Цилиндр называется вписанным в призму, если окружности его оснований вписаны в основания призмы, а боковая поверхность касается боковых граней призмы.

Теорема. Для того чтобы в призму можно было вписать цилиндр, необходимо и достаточно, чтобы призма была прямая и в ее основание можно было вписать окружность.

Конус называется описанным около пирамиды, если окружность основания конуса описана около основания пирамиды, а боковые ребра пирамиды являются образующими конуса. Пирамида соответственно называется вписанной в конус.

Теорема. Для того чтобы около пирамиды можно было описать конус, необходимо и достаточно, чтобы боковые ребра пирамиды были равны.

Конус называется вписанным в пирамиду, если окружность его основания вписана в основание пирамиды, а боковая поверхность касается боковых граней пирамиды. Пирамида соответственно называется описанной около конуса.

Теорема. Для того чтобы в пирамиду можно было вписать конус, необходимо и достаточно, чтобы в основание пирамиды можно было вписать окружность, а вершина пирамиды ортогонально проектировалась в центр этой окружности.

Задания для самостоятельного решения

1.1. В правильную четырехугольную пирамиду с объемом 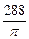вписан конус. Найдите его объем.

1.2. В конус, образующая которого наклонена к плоскости основания под углом a, вписана пирамида. Основание пирамиды – прямоугольный треугольник с катетами 3 см и 4 см. Найдите объем пирамиды, если

1.3. Около цилиндра описана правильная четырехугольная призма, периметр основания которого равен 12 см, а площадь боковой поверхности равна 48 см². Найдите площадь полной поверхности цилиндра.

1.4. В равносторонний цилиндр, диагональ осевого сечения которого равна вписана правильная шестиугольная призма. Вычислите площадь боковой поверхности призмы.

1.5. Усеченный конус описан около правильной треугольной усеченной пирамиды. Радиус верхнего основания в 2 раза меньше радиуса нижнего основания конуса, высота равна 4 см, а образующая 5 см. Найдите площадь боковой поверхности усеченной пирамиды.

1.6. В куб вписан шар и около куба описан шар. Найдите отношение объемов этих шаров.

1.7. В сферу вписан цилиндр. Площадь основания цилиндра 16 p см², тангенс угла наклона диагонали его осевого сечения к плоскости основания равен 3. Найдите площадь сферы.

1.8. В конус, площадь боковой поверхности которого в 2 раза больше площади основания, вписан шар. Найдите радиус шара, если образующая конуса равна 8 см.

1.9. В цилиндрическую мензурку, диаметр которой 2,5 см, заполненную водой до некоторого уровня, опускают четыре равных металлических шариков диаметром в 1 см. Определите, на сколько изменится уровень воды в мензурке.

1.10. Основание шарового слоя и цилиндра совпадают. Объем тела, заключенного между их боковыми поверхностями, равен 36 p см³. Найдите высоту шарового слоя.

Дата добавления: 2014-12-16