Шаровой слой и сферический пояс

Шаровой сегмент и сферический сегмент

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Круг, получившийся в сечении, называется основанием сегмента. Отрезок, соединяющий центр основания сегмента с точкой поверхности шара, перпендикулярный основанию, называется высотой шарового сегмента (рис. 41). Поверхность сферической части шарового сегмента называется сферическим сегментом.

Рис. 41

Для шарового сегмента верны формулы:

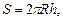
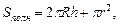
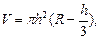
где R – радиус шара;

r – радиус основания шарового сегмента;

h – высота сегмента;

S – площадь сферической части шарового сегмента (площадь сферического сегмента);

S_полн - площадь полной поверхности шарового сегмента;

V – объем шарового сегмента.

Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями. Круги, получившиеся в сечении, называются основаниями слоя. Расстояние между секущими плоскостями называется высотой слоя (рис. 42). Поверхность сферической части шарового слоя называется сферическим поясом.

Шар, шаровой сегмент и шаровой слой можно рассматривать как геометрические тела вращения. При вращении полукруга вокруг оси, содержащей диаметр полукруга получается шар, соответственно при вращении частей круга получаются части шара: шаровой сегмент и шаровой слой.

Рис. 42

Для шарового слоя верны формулы:

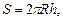
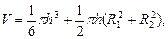
где R – радиус шара;

R₁, R₂ – радиусы оснований;

h – высота;

S₁, S₂ – площади оснований;

S – площадь сферической части шарового слоя (площадь сферического пояса);

S_полн – площадь полной поверхности;

V – объем шарового слоя.

Дата добавления: 2014-12-16