Обобщенный закон Ома

1. У ребенка судорожный синдром. Основанием для диагноза является наличие у ребенка клонико-тонических судорог.

а) вызвать к ребенку врача для оказания экстренной помощи (вызов третьим лицом).

б) уложить ребенка на пеленальный стол, обеспечив постоянное наблюдение для предупреждения травм ребенка во время судорог.

в) расстегнуть стесняющую одежду, отсосать слизь из носоглотки для улучшения дыхания.

г) дать увлажненный кислород ребенку для борьбы с гипоксией.

д) голову повернуть на бок, следить за положением языка, чтоб не было его западания во время судорог с последующей асфиксией.

е) подготовить 1,0 мл седуксена для введения ребенку по назначению врача.

ж) постоянно определять ЧСС, ЧДД, наблюдать за ребенком с целью контроля за состоянием.

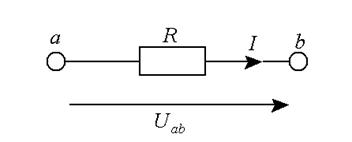
Закон Ома определяет связь между основными электрическими величинами на участке цепи постоянного тока без активных элементов (рис.1.1):

Обобщенный закон Ома определяет связь между основными электрическими величинами на участке цепи постоянного тока, содержащем резистор и идеальный источник ЭДС (рис.1.2):

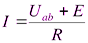Формула справедлива для указанных на рис.1.2 положительных направлений падения напряжения на участке цепи (U_ab), идеального источника ЭДС (Е) и положительного направления тока (I).

Правила Кирхгофа

Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях. Эти расчёты упрощаются, если пользоваться правилами Кирхгофа. Правил Кирхгофа два: правило токов и правило напряжений. Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:

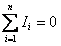. (7.9) Рис. 7.4. При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Так, для узла А (рис. 7.3.) можно записать: I ₁ – I ₂ – I ₃ + I ₄ – I ₅ = 0. Это первое правило Кирхгофа является следствием уравнения непрерывности (см. (6.7)) или закона сохранения электрического заряда. Правило напряжений относится к любому замкнутому контуру разветвлённой цепи. Выделим, например, в разветвлённой сложной цепи замкнутый элемент 1-2-3-1 (рис. 7.5.). Произвольно обозначим в ветвях контура направления токов I ₁, I ₂, I ₃. Для каждой ветви запишем уравнение закона Ома для неоднородного участка цепи: Участок

. Здесь R ₁, R ₂, R ₃ — полное сопротивление соответствующих ветвей. Сложив эти уравнения, получим формулу второго правила Кирхгофа: I ₁ R ₁ – I ₂ R ₂ – I ₃ R ₃ = e₁ + e₂ – e₃ – e₄ + e₅. Правило напряжений формулируется так: в любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с., встречающихся в этом контуре:

. (7.10) Рис. 7.5. При составлении уравнения (7.10) второго правила Кирхгофа задаются направлением обхода: в нашем примере — по часовой стрелке. Токи, совпадающие с направлением обхода, берутся со знаком плюс (I ₁), токи противоположного направления — со знаком минус (– I ₂, – I ₃). Э.д.с. источника берётся со знаком плюс, если он создаёт ток, совпадающий с направлением обхода (+e₁, +e₂, +e₅). В противном случае э.д.с. отрицательна (–e₃, –e₄). В качестве примера составим уравнения правил Кирхгофа для конкретной электрической схемы — измерительного моста Уитстона (рис. 7.6.). Мост образуют четыре резистора R ₁, R ₂, R ₃, R ₄. В точках A и B к мосту подключен источник питания (e, r), а в диагонали BD — измерительный гальванометр с сопротивлением R _g. Рис. 7.6. 1. Во всех ветвях схемы произвольно обозначим направления токов I ₁, I ₂, I ₃, I ₄, I _g, I _e. 2. В схеме четыре узла: точки A, B, C, D. Для трёх из них составим уравнения первого правила Кирхгофа — правила токов: точка А: I _e – I ₁ – I ₄ = 0; (1) точка B: I ₁ – I ₂ – I _g = 0; (2) точка D: I ₄ + I _g – I ₃ = 0. (3) 3. Для трёх контуров цепи ABDA, BCDB и ADC e A составим уравнения второго правила Кирхгофа. Во всех контурах направление обхода по часовой стрелке. ABDA: I ₁ R ₁ + I _g R _g – I ₄ R ₄ = 0; (4) BCDB: I ₂ R ₂ – I ₃ R ₃ – I _g R _g = 0; (5) ADC e A: I ₄ R ₄ + I ₃ R ₃ + I _e r = e. (6) Таким образом, мы получили систему шести уравнений, решая которую можно найти все шесть неизвестных токов. Но чаще мост Уитстона используется для измерения неизвестного сопротивления R_x º R ₁. В этом случае резисторы R ₂, R ₃и R ₄ — переменные. Меняя их сопротивления, добиваются того, чтобы ток в измерительной диагонали моста оказался равным нулю I _g = 0. Это означает, что: I ₁ = I ₂ см. (1), I ₃ = I ₄ см. (3), I ₁ R ₁ = I ₄ R ₄ см. (4), I ₂ R ₂ = I ₃ R ₃ см. (5). Учитывая эти упрощающие обстоятельства, приходим к выводу, что:

, или:

. Замечательно, что для определения неизвестного сопротивления нужно знать лишь сопротивления резисторов моста R ₂, R ₃ и R ₄. Э.д.с. источника, его внутреннее сопротивление, как и сопротивление гальванометра при таком измерении не играют никакой роли.

22.Работа и мощность тока. Закон Джоуля – Ленца в интегральной и дифференциальной формах.