Правило Ленца

Закон электромагнитной индукции

Электродвижущая сила, индуцируемая в проводящем контуре, равна скорости изменения магнитного потока, сцепляющегося с этим контуром.

В катушке, которая имеет несколько витков, общая ЭДС зависит от количества витков n:

Но в общем случае, применяют формулу ЭДС с общим потокосцеплением:

ЭДС возбуждаемая в контуре, создает ток. Наиболее простым примером появления тока в проводнике является катушка, через которую проходитпостоянный магнит. Направление индуцируемого тока можно определить с помощью правила Ленца.

Ток, индуцируемый при изменении магнитного поля проходящего через контур, своим магнитным полем препятствует этому изменению.

В том случае, когда мы вводим магнит в катушку, магнитный поток в контуре увеличивается, а значит магнитное поле, создаваемое индуцируемым током, по правилу Ленца, направлено против увеличения поля магнита. Чтобы определить направление тока, нужно посмотреть на магнит со стороны северного полюса. С этой позиции мы будем вкручивать буравчик по направлению магнитного поля тока, то есть навстречу северному полюсу. Ток будет двигаться по направлению вращения буравчика, то есть по часовой стрелке.

В том случае, когда мы выводим магнит из катушки, магнитный поток в контуре уменьшается, а значит магнитное поле, создаваемое индуцируемым током, направлено против уменьшения поля магнита. Чтобы определить направление тока, нужно выкручивать буравчик, направление вращения буравчика укажет направление тока в проводнике – против часовой стрелки.

35.Самоиндукция. Индуктивность. Индуктивность соленоида.

а прошлой лекции были рассмотрены магнитные поля прямолинейного тока , соленоида (B = m₀ nI (9.17)) и тороида .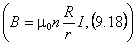

Индукция каждого из этих полей пропорциональна силе тока, создающего поле.

В соленоиде поле однородно и вычислить поток вектора магнитной индукции, пронизывающий N витков соленоида, особенно просто:

.

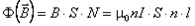Напомним, что здесь l, S — длина и площадь сечения соленоида, n = — число витков на единице длины соленоида.

. (10.4)

Магнитный поток, пронизывающий витки соленоида, пропорционален току, протекающему по его обмотке.

Можно показать, что этот частный результат справедлив не только для соленоида, но и для любого электрического контура.

Ток, обтекающий контур, создаёт магнитное поле. Это поле пронизывает контур, создавая поток, который пропорционален величине тока. Коэффициент пропорциональности, связывающий магнитный поток, пронизывающий контур, с током, протекающим по тому же самому контуру, называется индуктивностью контура L.

Например, индуктивность соленоида, как следует из (10.4):

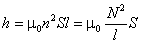(10.5)

Индуктивность любого контура зависит от его размеров и геометрии. В случае соленоида индуктивность определяется длиной и поперечным сечением соленоида, числом витков на единице длины (n), или полным числом витков N.

В системе СИ индуктивность измеряется в генри (Гн):

.

Теперь представим себе, что мы имеем возможность менять ток в соленоиде, передвигая ползунок А делителя напряжения (рис. 10.9.).

Рис.10.9.

Ток, протекающий в соленоиде, создаёт в нём магнитное поле. Это поле обеспечивает поток (см. 10.4.), причём скорость изменения магнитного потока будет пропорциональна скорости изменения тока:

.

Но изменение магнитного потока, пронизывающего замкнутый контур — единственное условие возникновения э.д.с. индукции:

.

Так как в данном случае изменение потока обусловлено изменением собственного тока, это явление электромагнитной индукции получило название явление самоиндукции:

. (10.6)

Э.д.с. самоиндукции пропорциональна скорости изменения тока в контуре. Закон самоиндукции (10.6) позволяет так определить единицу индуктивности 1 Гн:

.

1 генри — индуктивность такого контура, в котором возникает э.д.с. самоиндукции 1 В при скорости изменения тока в контуре 1 А/с.

36. Экстратоки замыкания и размыкания. Законы установления тока.

При всяком изменении силы тока в каком-либо контуре в нем возникает ЭДС самоиндукции, которая вызывает появление в этом контуре дополнительных токов, называемых экстратоками. По правилу Ленца экстратоки, возникающие в проводниках вследствие самоиндукции, всегда направлены так, чтобы воспрепятствовать изменению тока, текущего в цепи. В схеме опыта, приведенной на рис.14.7, при замыкании ключа (положение 1) в катушке возникает экстраток замыкания, направление которого противоположно нарастающему току батареи. При этом часть экстратока замыкания ответвляется на батарею, а часть на гальванометр, где его направление совпадает с направлением тока батареи – гальванометр дает дополнительный отброс вправо.

1 – замыкание ключа:

2 - размыкание ключа:

Рис.14.7. Экстратоки замыкания и размыкания.

При размыкании ключа (положение 2) магнитный поток в катушке начнет исчезать. В ней возникнет экстраток размыкания, который будет препятствовать убыванию магнитного потока, то есть будет направлен в катушке в ту же сторону, что и убывающий ток. При этом экстраток размыкания теперь целиком проходит через гальванометр, где его направление противоположно направлению первоначального тока – гальванометр дает отброс влево.

Установление и исчезновение тока в цепи, содержащей индуктивность, происходит не мгновенно, а постепенно. Рассмотрим электрическую цепь, состоящую из источника ЭДС , катушки индуктивности L и сопротивления R (рис.14.8). При размыкании ключа в образующейся замкнутой цепи помимо ЭДС будет действовать ЭДС самоиндукции . По второму правилу Кирхгофа можем написать: или в виде

.

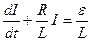Решением полученного дифференциального уравнения, полагая, что в начальный момент времени t = 0 ток отсутствовал I (0)=0, является функция:

,

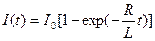где .

График этой функции приведен на рис.14.8 (кривая 1). Видим, что установление тока в цепи происходит не мгновенно, а с некоторым запаздыванием. Характерное время 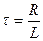называется временем ретардации (запаздывания, задержки).

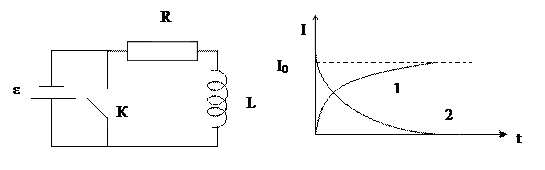
Рис.14.8. Установление и исчезновение тока в цепи, содержащей индуктивность.

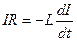При замыкании ключа образуется контур, содержащий только индуктивность L и сопротивление R (источник ЭДС при этом блокируется). Теперь в цепи действует только ЭДС самоиндукции , и по закону Ома: или в виде

.

Решением этого уравнения, считая, что в начальный момент времени t = 0 ток имел максимальное значение, равное , является функция:

.

График ее приведен на рис.14.8 (кривая 2). Видим, что исчезновение тока в цепи происходит не мгновенно, но с запаздыванием.

Характерное время 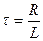называется в этом случае временем релаксации (восстановления).

37.Энергия магнитного поля.

Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна

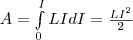
Значит, энергия магнитного поля, которое связано с контуром,

(1)

Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем

Так как I=B l /(μ₀μN) и В=μ₀μH, то

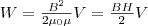(2)

где S l = V — объем соленоида.

Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью

(3)

Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н, т.е. оно относится только к пара- и диамагнетикам.

38.Магнитные свойства вещества. Молекулярные токи. Магнитные моменты атомов. Магнитный момент магнетика.

Глава 16 Магнитные свойства вещества

§ 131. Магнитные моменты электронов и атомов

Рассматривая действие магнитного поля на проводники с током и на движущиеся

заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды

учитывались формально с помощью магнитной проницаемости . Для того чтобы

разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо

рассмотреть действие магнитного поля на атомы и молекулы вещества.

Опыт показывает, что все вещества, помещенные в магнитное поле, намагничиваются.

Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в

основу гипотезу Ампера (см. § 109), согласно которой в любом теле существуют

микроскопические токи,

обусловленные движением электронов в атомах и молекулах.

Для качественного объяснения магнитных явлений с достаточным приближением

можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся

по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным

магнитным моментом (см. (109.2)) pm = ISn, модуль которого

pm=IS=evS, (131.1)

где I = ev — сила тока, v — частота вращения электрона по орбите, S — площадь

орбиты. Если электрон движется по часовой стрелке (рис. 187), то ток направлен против

часовой стрелки и вектор рm в соответствии с правилом правого винта направлен

перпендикулярно плоскости орбиты электрона.

С другой стороны, движущийся по орбите электрон

обладает механическим моментом импульса Le, модуль

которого, согласно (19.1),

Le=mvr=2mvS, (131.2)

где v=2vr, r

2=S. Вектор Le (его направление также

подчиняется правилу правого винта), называется

орбитальным механическим моментом электрона.

Из рис. 187 следует, что направления рm и Le

противоположны, поэтому, учитывая выражения (131.1) и

(131.2), получим

pm=-(e/2m)Le=gLe, (131.3)

где величина

g=-e/2m (131.4)

называется гиромагнитным отношением

орбитальных моментов (общепринято писать со знаком «-», указывающим на то, что

направления моментов противоположны). Это отношение, определяемое универсальными

постоянными, одинаково для любой орбиты, хотя для разных орбит значения v и r различны.

Формула (131.4) выведена для круговой орбиты, но она справедлива и для эллиптических

орбит. Экспериментальное определение гиромагнитного отношения проведено в опытах

Эйнштейна и де Гааза (1915), которые наблюдали поворот свободно подвешенного на

тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном

поле (по обмотке соленоида пропускался переменный ток с часто-

той, равной частоте крутильных колебаний стержня). При исследовании вынужденных

крутильных колебаний стержня определялось гиромагнитное отношение, которое оказалось

равным — (е/т). Таким образом, знак носителей, обусловливающих молекулярные токи,

совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза

большим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата,

имевшего большое значение для дальнейшего развития физики, было предположено, а

впоследствии доказано, что кроме орбитальных моментов (см. (131.1) и (131.2)) электрон

обладает собственным механическим моментом импульса Les, называемым спином.

Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к

целому ряду противоречий. В настоящее время установлено, что спин являетсянеотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона Les

соответствует собственный (спиновый) магнитный момент pms, пропорциональный Les и

направленный в противоположную сторону:

pms=gsLes. (131.5)

Величина gs называется гиромагнитным отношением спиновых моментов.

Проекция собственного магнитного момента на направление вектора В может

принимать только одно из следующих двух значений:

где h=h/(2) (h — постоянная Планка), в — магнетон Бора, являющийся единицей

магнитного момента электрона.

В общем случае магнитный момент электрона складывается из орбитального и

спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из

магнитных моментов входящих в его состав электронов и магнитного момента ядра

(обусловлен магнитными моментами входящих в ядро протонов и нейтронов). Однако

магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому

ими пренебрегают.

Таким образом, общий магнитный момент атома (молекулы) ра равен векторной сумме

магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:

pа=рm+рms. (131.6)

Еще раз обратим внимание на то, что при рассмотрении магнитных моментов

электронов и атомов мы пользовались классической теорией, не учитывая ограничений,

накладываемых на движение электронов законами квантовой механики. Однако это не

противоречит полученным результатам, так как для дальнейшего объяснения

намагничивания веществ существенно лишь то, что атомы обладает магнитными моментами

39.Намагниченность. Магнитная восприимчивость. Индукция поля в веществе. Магнитная проницаемость вещества.

Подобно тому, как для количественного описания поляризации диэлектриков вво-

дилась поляризованность (см. §88), для количественного описания намагничения магнетиков

вводят векторную величину — намагниченность, определяемую магнитным моментом

единицы объема магнетика:

J=pm/V=pa/V,

где pm=ра— магнитный момент маг-нетика, представляющий собой векторную сумму

магнитных моментов отдельных молекул (см. (131.6)).

Рассматривая характеристики магнитного поля (см. §109), мы вводили вектор

магнитной индукции В, характеризующий результирующее магнитное поле, создаваемое

всеми макро- и микротоками, и вектор напряженности Н, характеризующий магнитное поле

макротоков. Следовательно, магнитное поле в веществе складывается их двух полей:

внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом. Тогда

вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной

сумме магнитных индукций внешнего поля В0 (поля, создаваемого намагничивающим током

в вакууме) и поля микротоков В' (поля, создаваемого молекулярными токами):

В = В0+В', (133.1)

где В0=0Н (см. (109.3)).

Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде

кругового цилиндра сечения S и длины l, внесенного в однородное внешнее магнитное поле с

индукцией Во. Возникающее в магнетике магнитное поле молекулярных токов будет

направлено противоположно внешнему полю для диамагнетиков и совпадать с ним понаправлению для парамагнетиков. Плоскости всех молекулярных токов расположатся

перпендикулярно вектору Во, так как векторы их магнитных моментов рm антипараллельны

вектору В0 (для диамагнетиков) и параллельны Во (для парамагнетиков). Если рассмотреть

любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения

магнетика молекулярные токи соседних атомов направлены навстречу друг другу и взаимно

компенсируются (рис. 189). Нескомпенсированными будут лишь молекулярные токи,

выходящие на боковую поверхность цилиндра.

Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает

внутри него поле, магнитную индукцию В' которого

можно вычислить, учитывая формулу (119.2) для N=1

(соленоид из одного витка):

В' = 0I'/l (133.2)

где I' — сила молекулярного тока, l — длина

рассматриваемого цилиндра, а магнитная

проницаемость  принята равной единице.

С другой стороны, I'/l — ток, приходящийся на

единицу длины цилиндра, или его линейная плотность,

поэтому магнитный момент этого тока p=I'lS/l=I'V/l,

где V — объем магнетика. Если Р — магнитный момент

магнетика объемом V, то P/V — намагниченность

магнетика J. Таким образом,

J= I'/l. (133.3)

Сопоставляя (133.2) и (133.3), получим, что

B'=0J,

или в векторной форме

B'=0J.

Подставив выражения для В0 и В' в (133.1), получим

В =0Н+0J, (133.4) или

B/0=H+J. (133.5) Как показывает опыт, в несильных полях намагниченность прямо

пропорциональна напряженности поля, вызывающего намагничение, т. е.

J=H, (133.6)

где  — безразмерная величина, называемая магнитной восприимчивостью

вещества. Для диамагнетиков  отрицательна (поле молекулярных токов противоположно

внешнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с

внешним).

Используя формулу (133.6), выражение (133.4) можно записать в виде

В = 0(1+)Н, (133.7) откуда

Н=B/0(1+).

Безразмерная величина

=1+ (133.8)

представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7),

придем к соотношению (109.3) В=0Н, которое ранее постулировалось.

Так как абсолютное значение магнитной восприимчивости для диа- и парамагнетиков

очень мало (порядка 10

-4— 10

-6

), то для них  незначительно отличается от единицы. Это

просто понять, так как магнитное поле молекулярных токов значительно слабее

намагничивающего поля. Таким образом, для диамагнетиков <0 и <1, для парамагнетиков

>0 и >1.

Закон полного тока для магнитного поля в веществе (теорема о циркуляции

вектора В) является обобщением закона (118.1):

где I и I' — соответственно алгебраические суммы макротоков (токов проводимости) и

микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.Таким образом, циркуляция вектора магнитной индукции В по произвольному замкнутому

контуру равна алгебраической сумме токов проводимости и молекулярных токов,

охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, таким

образом, характеризует результирующее поле, созданное как макроскопическими токами в

проводниках (токами проводимости), так и микроскопическими токами в магнетиках,

поэтому линии вектора магнитной индукции В не имеют источников и являются

замкнутыми.

Можно доказать, что циркуляция намагниченности J по произвольному замкнутому

контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:

Тогда закон полного тока для магнитного поля в веществе можно записать также в виде

где I, подчеркнем это еще раз, есть алгебраическая сумма токов проводимости.

Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как

введенный ранее вектор Н напряженности магнитного ноля. Итак, циркуляция вектора Н по

произвольному замкнутому контуру L равна алгебраической сумме токов проводимости,

охватываемых этим контуром:

Выражение (133.10) представляет собой теорему о циркуляции вектора Н.

40.Диа- и парамагнетизм. Объяснение свойств.

Всякое вещество является магнетиком, т. е. оно способно под действием магнитного

поля приобретать магнитный момент (намагничиваться). Для понимания механизма этого

явления необходимо рассмотреть действие магнитного поля на движущиеся в атоме

электроны.

Ради простоты предположим, что электрон в атоме

движется по круговой орбите. Если орбита электрона

ориентирована относительно вектора В произвольным образом,

составляя с ним угол а (рис. 188), то можно доказать, что она

приходит в такое движение вокруг В, при котором вектор

магнитного момента рm, сохраняя постоянным угол а, вращается

вокруг на-

правления В с некоторой угловой скоростью. Такое

движение в механике называется прецессией. Прецессию

вокруг вертикальной оси, проходящей через точку опоры,

совершает, например, диск волчка при замедлении движения.

Таким образом, электронные орбиты атома под действием

внешнего магнитного поля совершают прецессионное движение,

которое эквивалентно круговому току. Так как этот микроток

индуцирован внешним магнитным полем, то, согласно правилу

Ленца, у атома появляется составляющая магнитного поля,

направленная противоположно внешнему полю. Наведенные

составляющие магнитных полей атомов (молекул) складываются и образуют собственное

магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил

название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном

поле против направления поля, называются диамагнетиками.В отсутствие внешнего магнитного поля диамагнетик немагнитен, поскольку в данном

случае магнитные моменты электронов взаимно компенсируются, и суммарный магнитный

момент атома (он равен векторной сумме магнитных моментов (орбитальных и спиновых)

составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы

(например, Bi, Ag, Au, Cu), большинство органических соединений, смолы, углерод и т. д.

Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на

электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с

диамагнитными веществами существуют и парамагнитные — вещества,

намагничивающиеся во внешнем магнитном поле по направлению поля.

У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные

моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнетиков

всегда обладают магнитным моментом. Однако вследствие теплового движения молекул их

магнитные моменты ориентированы беспорядочно, поэтому парамагнитные вещества

магнитными свойствами не обладают. При внесении парамагнетика во внешнее магнитное

поле устанавливается преимущественная ориентация магнитных моментов атомов по полю

(полной ориентации препятствует тепловое движение атомов). Таким образом, парамагнетик

намагничивается, создавая собственное магнитное поле, совпадающее по направлению с

внешним полем и усиливающее его. Этот эффект называется парамагнитным. При

ослаблении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие

теплового движения нарушается и парамагнетик размагничивается. К парамагнетикам

относятся редкоземельные элементы, Pt, Al и т. д. Диамагнитный эффект наблюдается и в

парамагнетиках, но он значительно слабее парамагнитного и поэтому остается незаметным.

Из рассмотрения явления парамагнетизма следует, что его объяснение совпадает с

объяснением ориентационной (дипольной) поляризации диэлектриков с полярными

молекулами (см. §87), только электрический момент атомов в случае поляризации надо

заменить магнитным моментом атомов в случае намагничения.

Подводя итог качественному рассмотрению диа- и парамагнетизма, еще раз отметим,

что атомы всех веществ являются носителями диамагнитных свойств. Если магнитный

момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и

вещество является парамагнетиком; если магнитный момент атомов мал, то преобладают

диамагнитные свойства и вещество является диамагнетиком.

Дата добавления: 2014-12-16