
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обобщение и конкретизация задач 2 страница
|
|
|
|
2. Участки двух дачников расположены на берегу реки. На этих участках установлены емкости для воды, используемой для полива. Соседи решили на берегу реки поставить насос и провести от него трубы к каждой из емкостей. Укажите, где нужно установить насос и как провести трубы, чтобы их расход был наименьшим.
Эти задачи, несмотря на различие формулировок, имеют одно и тоже математическое содержание: точки А и В расположены по одну сторону от прямой а. На прямой а нужно указать точку М такую, чтобы ломанная АМВ была наименьшей. Геометрическая модель задачи изображена на рисунке:

Если бы точки А и В лежали по разные стороны от прямой а, так как расположены точки А и С, то искомая точка М была бы пересечением отрезка АС и прямой а. Точки В и С симметричны относительно а. Поэтому АМ + МВ = АМ + МС = АС и точка М построена.
Составление математической модели – это наиболее распространенный вид обобщения. Он состоит в переводе происходящих в действительности процессов на язык математики.
Обобщение решения конкретных задач может дать единый метод целого класса однородных задач. Такой вариант обобщения хорошо просматривается при изучении пропорциональных зависимостей величин.
Скорость движения 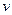 , время движения
, время движения 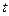 , пройденное расстояние
, пройденное расстояние 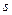 связаны формулами:
связаны формулами: 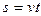 ,
,  ,
,  .
.
Цена товара Ц, количество товара К, стоимость С образуют аналогичные формулы: 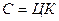 ,
, 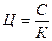 ,
, 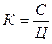 .
.
Производительность труда к, время работы t, объем работы A связаны друг с другом: 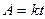 ,
, 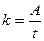 ,
, 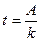 .
.
Плотность 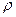 , масса m, объем вещества V вычисляются по формулам:
, масса m, объем вещества V вычисляются по формулам: 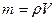 ,
,  ,
, 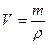 .
.
Легко заметить, что во всех рассмотренных случаях задачные ситуации описываются с помощью всего лишь двух математических формул: 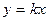 ,
, 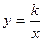 . Это и есть простейшие математические модели прямой и обратной пропорциональности.
. Это и есть простейшие математические модели прямой и обратной пропорциональности.
При решении и составлении математических задач часто применяют индуктивные обобщения. Суть индуктивного обобщения заключается в следующем. Рассматривается самый простой частный случай задачи, когда она решается легко. Решив эту задачу, обобщают ее на другой более сложный, но все же частный случай, используя результат предыдущей задачи. Обобщение происходит до тех пор, пока не получится задача, обобщающая все предыдущие.
Например.
1. Докажите, что сумма расстояний от любой точки М, находящейся на стороне правильного треугольника до его сторон равна длине высоты треугольника.
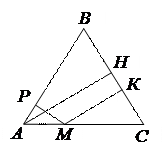
| 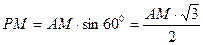 . .
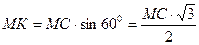 . .
 . .
|
2. Докажите, что сумма расстояний от любой точки М правильного треугольника до его сторон равна длине высоты треугольника.
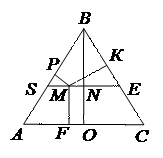
| Проведем через точку М прямую SE ║ АС.
Тогда треугольник SBE правильный.
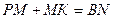 , , 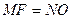 .
Следовательно, .
Следовательно, 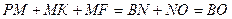 . .
|
Еще один пример – теорема Чевы.
Обобщение систематизирует знания учащихся, так как требует установления и осмысления взаимосвязи между понятиями и отношениями, о которых идет речь в задаче. В ходе выяснения таких взаимосвязей у учащихся составляется некий целостный образ, в котором одно знание следует из другого и связано с ним. В конце концов, некоторая группа знаний, расположенных в определенной последовательности по отношению друг к другу, составит систему.
В качестве примера рассмотрим обобщения при решении задач о геометрической прогрессии.
Компонентами задач о геометрической прогрессии являются числа:
 – первый член,
– первый член, 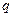 – знаменатель,
– знаменатель, 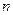 – число членов,
– число членов,  – n -й член,
– n -й член,
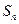 – сумма первых n членов прогрессии.
– сумма первых n членов прогрессии.
Между ними установлены два основных соотношения:
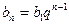 и
и 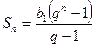 ,
, 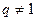 .
.
Если заданы три компонента из пяти, то два оставшихся могут быть вычислены.
Таким образом, возможные десять типов задач на геометрическую прогрессию определяются данными:
1)  ,
, 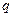 ,
, 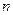 ; 2)
; 2)  ,
, 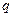 ,
,  ; 3)
; 3)  ,
, 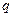 ,
, 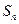 ; 4)
; 4)  ,
, 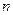 ,
,  ; 5)
; 5)  ,
, 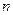 ,
, 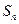 ;
;
6)  ,
,  ,
, 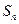 ; 7)
; 7) 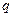 ,
, 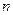 ,
,  ; 8)
; 8) 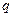 ,
, 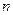 ,
, 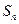 ; 9)
; 9) 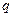 ,
,  ,
, 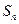 ; 10)
; 10) 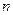 ,
,  ,
, 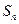 .
.
Задачи типа 2), 3), 6), 9) приводят к системам простейших показательных уравнений, а 4), 5), 10) задачи – к системам рациональных уравнений, остальные – к системам линейных уравнений.
Таким образом, выделены три основных метода решения задач на геометрическую прогрессию.
Обобщение может выступать и как переход от данного множества предметов к рассмотрению более «емкого» множества, содержащего данное.
Прием обобщения задачи включает в себя обобщение либо условия, либо требования, либо их частей. Исходная задача – доказать, что для сторон Δ АВС верно неравенство АВ+ВС>АС. Более общим понятием треугольника может быть тетраэдр. Рассмотрим тетраэдр АВСD. Напишем неравенство для каждой боковой грани тетраэдра: АВ+АС>СВ, АС+АD>DС, АD+АВ>ВD. Сложив левые и правые части неравенств, получим: АВ+АС+АD> 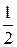 (ВD+СВ+DС). Сформулируем полученную задачу – доказать, что для ребер тетраэдра АВСD верно неравенство АВ+АС+АD>
(ВD+СВ+DС). Сформулируем полученную задачу – доказать, что для ребер тетраэдра АВСD верно неравенство АВ+АС+АD> 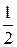 (ВD+СВ+DС), где АВ, АС, АD – ребра, исходящие из вершины А.
(ВD+СВ+DС), где АВ, АС, АD – ребра, исходящие из вершины А.
«Распространим» теорему Пифагора на пространственный случай. Используя построенные ранее закономерные переходы от одного пространства к другому, длину отрезка соотнесем с площадью фигуры, треугольник с треугольной пирамидой. Вместо перпендикулярности сторон в пространственном случае можно рассмотреть прямые углы при вершине пирамиды. В результате получится следующее обобщение теоремы: «Дана треугольная пирамида, плоские углы при вершине которой прямые. Докажите, что квадрат площади основания пирамиды равен сумме квадратов площадей боковых граней», причем построенная пространственная теорема тоже выполняется.
Рассмотрим еще один пример. Докажите, что 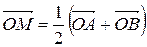 , где О – произвольная точка пространства, а М – середина отрезка АВ. Во всех учебниках геометрии эту задачу используют в качестве иллюстрации применения векторного метода: выразив ОМ через векторы ОА и АМ, а также через векторы О В и ВМ, затем, сложив полученные векторные равенства и выполнив небольшие преобразования, получим требуемый результат.
, где О – произвольная точка пространства, а М – середина отрезка АВ. Во всех учебниках геометрии эту задачу используют в качестве иллюстрации применения векторного метода: выразив ОМ через векторы ОА и АМ, а также через векторы О В и ВМ, затем, сложив полученные векторные равенства и выполнив небольшие преобразования, получим требуемый результат.
Замечаем, что приведенные рассуждения можно использовать в случае замены в условии задачи отрезка треугольником: докажите, что  , где О – произвольная точка пространства, а М – точка пересечения медиан треугольника АВС.
, где О – произвольная точка пространства, а М – точка пересечения медиан треугольника АВС.
Стремление к дальнейшему обобщению задачи приводит к замене треугольника многоугольником или многогранником, что обусловливает и новое требование задачи: доказать, что 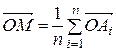 , где Аi – вершины многоугольника или многогранника. Анализируя все преобразования условия задачи, видим, что они осуществляются вокруг основной идеи: точка M должна быть центром тяжести. Это условие и определяет направление обобщения.
, где Аi – вершины многоугольника или многогранника. Анализируя все преобразования условия задачи, видим, что они осуществляются вокруг основной идеи: точка M должна быть центром тяжести. Это условие и определяет направление обобщения.
Обобщать можно не только геометрические задачи, связанные с построениями, но и задачи на нахождение. Для примера можно рассмотреть обобщение следующей задачи: «Найдите отношение периметра квадрата к сумме его диагоналей», не выходя за рамки двухмерного пространства.
Искомое отношение обозначим k. Сначала найдем k для прямоугольника, ромба, параллелограмма, а затем и для произвольного выпуклого четырехугольника. Но, если в исходной задаче k= 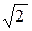 , т.е. не зависит от введенных по ходу решения параметров, то в остальных задачах такое отношение зависит от элементов четырехугольника и в большинстве случаев трудно найти хорошую формулу, зависящую от наименьшего количества параметров. Следовательно, нужно либо доопределять каждую предложенную задачу (они сразу становятся не интересными для решения), либо искать другое обобщение.
, т.е. не зависит от введенных по ходу решения параметров, то в остальных задачах такое отношение зависит от элементов четырехугольника и в большинстве случаев трудно найти хорошую формулу, зависящую от наименьшего количества параметров. Следовательно, нужно либо доопределять каждую предложенную задачу (они сразу становятся не интересными для решения), либо искать другое обобщение.
Числовые значения k имеют не слишком широкий разброс. В прямоугольнике, например, при стремлении одной из сторон к 0, значение k приближается к 1 (k > 1). Если же одну из диагоналей ромба взять близкой к 0, то k будет приближаться к 2 (k < 2). В параллелограмме при стремлении стороны к 0 значение k близко к 1, а если длина одной диагонали близка к 0, k» 2. В произвольном выпуклом четырехугольнике при стремлении одной диагонали к 0 (или, что то же самое, при стремлении длин двух смежных сторон к 0) k» 2, k < 2. Если к нулю стремятся две противоположные стороны, k» 1, k > 1.
В результате можно выбрать следующее обобщение задачи: «Доказать, что в выпуклом четырехугольнике отношение 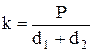 периметра к сумме диагоналей лежит в промежутке (1; 2), т.е. 1 < k < 2».
периметра к сумме диагоналей лежит в промежутке (1; 2), т.е. 1 < k < 2».
Заметим, что при формулировании условия задачи, значение k оценивалось приблизительно. Для доказательства сформулированного утверждения не обязательно пользоваться такой же оценкой (этот факт можно доказать, используя неравенства треугольника). Приблизительную оценку k можно применить для доказательства того, что нельзя сузить промежуток изменения значения k (значение k сколь угодно близко приближается и к 1, и к 2). Предлагаемое нами обобщение для учащихся не привычно, сформулированная задача слишком отличается от исходной (даже тип задачи изменился: на базе задачи на нахождение строится задача на доказательство). Также в ходе поиска обобщения приходится пользоваться методом крайних случаев, который многие учащиеся не умеют применять при решении задач. Поэтому при решении задачи лучше выбрать фронтальную форму работы.
Обратный по отношению к обобщению процесс происходит при применении конкретизации.
Исходная задача – найдите длины медиан ΔАВС, если его стороны равны a,b,c. Конкретизируя вид треугольника (прямоугольный, равнобедренный, равносторонний), получаем задачи, разного уровня сложности. Заметим, что по отношению новых задач исходная задача является задачей-обобщением полученных.
Приведем еще один пример конкретизации. AB и CD пересекаются в точке М. Точки A, B, C, D лежат на окружности. Доказать, что 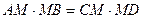 . Конкретизируя – где располагается точка М – внутри или вне окружности, получим свойства хорд и секущих. Доказательства обоих утверждений аналогичные (докажите самостоятельно). Совместное решение этих задач позволит сэкономить учебное время.
. Конкретизируя – где располагается точка М – внутри или вне окружности, получим свойства хорд и секущих. Доказательства обоих утверждений аналогичные (докажите самостоятельно). Совместное решение этих задач позволит сэкономить учебное время.
 | |||
 | |||
Далее можно рассмотреть частный случай первой задачи: одна из хорд (пусть АВ) является диаметром окружности, а другая (пусть хорда СD) перпендикулярна ей. Тогда 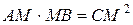 . В данной ситуации наиболее важным является формулировка решенной задачи: если из некоторой точки окружности опустить перпендикуляр на диаметр, то квадрат перпендикуляра равен произведению отрезков диаметра. (Перпендикуляр, опущенный из некоторой точки окружности на диаметр, есть среднее пропорциональное между отрезками диаметра.) Заметив, что вписанный угол, опирающийся на диаметр, прямой, ситуацию, отраженную в задаче, можно интерпретировать следующим образом: если из вершины прямого угла опустить перпендикуляр на гипотенузу, то квадрат перпендикуляра равен произведению отрезков гипотенузы.
. В данной ситуации наиболее важным является формулировка решенной задачи: если из некоторой точки окружности опустить перпендикуляр на диаметр, то квадрат перпендикуляра равен произведению отрезков диаметра. (Перпендикуляр, опущенный из некоторой точки окружности на диаметр, есть среднее пропорциональное между отрезками диаметра.) Заметив, что вписанный угол, опирающийся на диаметр, прямой, ситуацию, отраженную в задаче, можно интерпретировать следующим образом: если из вершины прямого угла опустить перпендикуляр на гипотенузу, то квадрат перпендикуляра равен произведению отрезков гипотенузы.
Будем исследовать задачную ситуацию, взяв предельный случай, который дает совпадение точек, например, А и В. Этот случай трансформирует задачу в следующую: через точку М проведены касательная МА (А – точка касания) и секущая, которая пересекает окружность в точках С и D. Докажите, что  .
.
Можно предложить самим учащимся сформулировать задачу, соответствующую описанной выше ситуации.
Второй предельный случай заданной ситуации (совпадение точек С и D) соответствует следующей задаче: из точки М проведены к окружности две касательные МА и МС (А и С— точки касания). Докажите, что МА=МС. Дальнейшее развитие задачи см. Саранцев Г.И. Обучение математическим доказательствам и опровержениям в школе. – М.: Гуманитар. Изд. Центр ВЛАДОС, 2005. – Гл. III, п.2.
Формулировка приведенной задачи без указания положения точки М является примером вариативной задачи, то есть задачи, которая предполагает рассмотрение нескольких задачных ситуаций с одинаковыми условиями, но различными вариантами чертежа.
Вопросы и задания
1. Законспектируйте материал о роли и месте обобщения и конкретизации при обучении математике:
а) Эрдниев П.М. Сравнение и обобщение при обучении математике. – М.: Знание, 1970.
б) Малых Е.В. Некоторые случаи применения обобщений // Математика в школе. – №6. – 2003 – с.38-40.
в) Саранцев Г.И. Обучение математическим доказательствам и опровержениям в школе. – М.: Гуманитар. Изд. Центр ВЛАДОС, 2005. – Гл. III, п.2.
2. Составьте задачу-обобщение к следующим задачам: решите с помощью тригонометрического круга уравнения:
а)  ; б)
; б)  ; в)
; в) 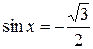
г) 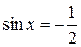 ; д)
; д) 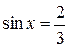 ; е)
; е) 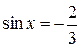
3. Составьте задачу-обобщение к следующим задачам:
а) Докажите, что биссектриса угла 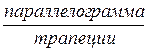 отсекает от него равнобедренный треугольник.
отсекает от него равнобедренный треугольник.
б) В прямоугольнике АВСD через точку О пересечения диагоналей проведена прямая, пересекающая стороны АВ и СD в точках М и N соответственно. Докажите, что отрезки МО и NО равны.
4. Дана задача: вывести формулу для вычисления радиуса окружности, вписанной в правильный треугольник. Используя приемы конкретизации и обращения, составьте две – три вычислительные задачи.
5. Обобщите формулу 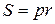 на любой описанный многоугольник и описанный многогранник.
на любой описанный многоугольник и описанный многогранник.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1840; Нарушение авторских прав?; Мы поможем в написании вашей работы!