
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи с несформированным требованием
|
|
|
|
Рассмотрим задачи, в которых имеются все данные, но нет требования.
Если ученик научится подбирать и формулировать вопрос (требование) к задаче, в которой полностью обозначено начальное состояние предмета, он лучше будет продвигаться по этапам решения задачи. Прежде чем выдвигать требование, нужно проанализировать данные, связать их между собой, выяснить, какие величины в принципе можно найти при таком условии, а затем уже можно строить вопрос. Если ученик попытается сформулировать вопрос, не вникая в заданные условия, не составив математическую модель задачи, это может привести к постановке вопроса, разрешить который тяжело из-за громоздкости вычислений при решении, или вообще невозможно из-за нехватки данных.
Одно из требований, предъявляемых к формулируемым учащимися задачам, - обязательная зависимость ответа от всех исходных данных. Это затрудняет работу по составлению, но приводит к более подробному и скрупулезному изучению связей между элементами задачи. Второе требование - так подобрать вопрос, чтобы не всегда легко находились вычисляемые значения, чтобы вопрос не лежал на поверхности, был не слишком очевиден.
Если ученики затрудняются в выборе интересных вопросов, преподаватель может сам привести несколько вариантов требований, а ученику предложить выбрать и обосновать выбор. Затем уже целесообразно перейти к самостоятельному выдвижению вопросов учащимися, сравнению результатов их работы.
Начать следует с задач, в которых очевидно, какие величины можно искать, причем, нетрудно записать соотношения для их нахождения.
Пример 1. Дано неполное условие задачи «Из пункта A и B, расстояние между которыми 18 км, навстречу друг другу вышли два пешехода и встретились в 10 км от пункта A через 2 часа после выхода». Сформулируйте вопрос к задаче.
При таком перечислении данных задачи можно легко найти и скорости пешеходов, и расстояния, которые прошел каждый из пешеходов до встречи, а время движения - это вообще известная величина. Если поставить вопрос только о нахождении расстояния, то при решении задачи будут использованы не все данные, что противоречит выдвинутому требованию.
Итак, пусть x, y км/ч - скорости пешеходов. Тогда 2x км прошел первый пешеход до встречи, что равно 10 км, т.е. 2x = 10, откуда x = 5. Второй пешеход до встречи прошел 2y км, что равно 8 км, т.е. 2y = 8, откуда y = 4.
Далее следует рассмотреть задачи, в которых можно найти значения нескольких различного рода величин.
Пример 2. Подберите требование к условию задачи «Две стороны параллелограмма относятся как 3:5, а его периметр равен 192 см. Высота, опущенная на его большую сторону, равна 24 см».
Чтобы выдвинуть требование, нужно выяснить, какие величины находятся, исходя из данных задачи. Можно поставить вопрос о нахождении сторон параллелограмма, но тогда не понятно, для чего дана длина высоты. Действительно, если обозначить за x и y соответственно меньшую и большую стороны параллелограмма, тогда  , т.е.
, т.е. 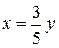 . Поскольку периметр P = 2(x+y) = 192, тогда
. Поскольку периметр P = 2(x+y) = 192, тогда  , откуда y = 60 (см), x = 36 (см).
, откуда y = 60 (см), x = 36 (см).
Чтобы использовать данную в условии высоту, можно добавить требование найти площадь параллелограмма или, например, найти неизвестную высоту параллелограмма.
Площадь 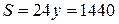 (см2). Высоту h, опущенную на меньшую сторону параллелограмма, можно найти, зная площадь. Действительно,
(см2). Высоту h, опущенную на меньшую сторону параллелограмма, можно найти, зная площадь. Действительно,  , т.е.
, т.е.  , откуда h = 40 (см).
, откуда h = 40 (см).
Пример 3. Подберите требование к условию задачи «В треугольнике ABC стороны AB =  , BC = 4, CA = 5. На стороне BC взята точка D так, что BD = 1».
, BC = 4, CA = 5. На стороне BC взята точка D так, что BD = 1».
В треугольнике ABC можно найти все углы, его периметр и площадь, радиусы вписанной и описанной окружностей. Но в условии еще задан отрезок BD, следовательно, нужно придумать требование, в котором «участвует» этот отрезок. Например, можно выяснить, чему равна длина отрезка AD, угол между AD и стороной BC, площадь треугольника ABD.
Обозначим AD = x, Ð ADC = a, тогда по теореме косинусов для треугольников ACD и ABD имеем:
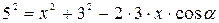 ,
,  ;
;
 ,
,  .
.
Из левой и правой частей второго уравнения вычтем соответствующие части первого, получим:  . Поскольку x≠ 0, тогда
. Поскольку x≠ 0, тогда 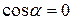 , т.е. a = 90°. Очевидно,
, т.е. a = 90°. Очевидно, 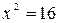 , откуда AD = x = 4.
, откуда AD = x = 4.
Наряду с предыдущими, следует рассмотреть задачи, в которых не всегда можно найти с виду легко вычисляемые величины.
Пример 4. Подберите требование к условию задачи «Два мотоциклиста выехали навстречу друг другу из пунктов A и B соответственно. Они встретились на расстоянии 18 км от A. После встречи мотоциклисты продолжили путь. Когда второй прибыл в A, первый не доехал 15 км до B».
Даже после составления математической модели ученики, которые отнесутся к задаче формально, могут ошибочно поставить вопрос о нахождении скоростей мотоциклистов. При указанных данных невозможно найти сами скорости, которые не определены, можно лишь однозначно найти отношение этих скоростей. Самый простой вопрос, который присоединяется к такому условию, - это «найти расстояние между A и B».
Пусть x, y км/ч - скорости мотоциклистов, S - расстояние AB. Тогда первый мотоциклист до встречи проехал 18 км за 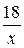 часов, второй мотоциклист проехал расстояние (S- 18) км за
часов, второй мотоциклист проехал расстояние (S- 18) км за 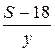 часов. Поскольку мотоциклисты затратили до встречи одно и то же время, то
часов. Поскольку мотоциклисты затратили до встречи одно и то же время, то 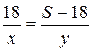 .
.
После встречи мотоциклисты продолжили движение. Второй проехал 18 км за 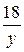 часов, первый проехал (S -18-15) км за
часов, первый проехал (S -18-15) км за  часов. Опять мотоциклисты затратили одно и то же время на движение, поэтому
часов. Опять мотоциклисты затратили одно и то же время на движение, поэтому  . Мы получили два уравнения с тремя неизвестными, откуда нельзя найти однозначно x и y, но можно найти их отношение и расстояние S. Действительно,
. Мы получили два уравнения с тремя неизвестными, откуда нельзя найти однозначно x и y, но можно найти их отношение и расстояние S. Действительно,  , откуда
, откуда 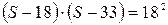 ,
, 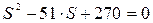 . Получаем, что S = 6 или S = 45. По условию задачи подходит решение S = 45 км.
. Получаем, что S = 6 или S = 45. По условию задачи подходит решение S = 45 км.
Заметим, что  , что возможно при различных подходящих скоростях x и y.
, что возможно при различных подходящих скоростях x и y.
Если ищем только расстояние от A до B, то можно сразу составить отношение, не вводя x и y: 
Приведенные выше примеры показывают, что для задачи с несформированным требованием можно сформулировать несколько вопросов, соподчиненность которых очевидна. Таким образом, происходит конструирование системы задач, имеющих одинаковое условие.
Сформулированная преподавателем система задач имеет важный методический аспект. Она показывает, что должны знать и уметь школьники в результате изучения конкретной темы. Без этого невозможно проектировать методическую систему учителя по изучению данной темы.
Сформулированная учеником система задач является средством диагностики знаний, умений и навыков по изученной теме.
Рассмотрим некоторые вопросы методики использования задач с несформированным требованием.
Например, перед учащимися ставиться задача: «На основании синтеза предложений  сформулировать как можно больше положений о взаимном расположении прямых и плоскостей».
сформулировать как можно больше положений о взаимном расположении прямых и плоскостей».
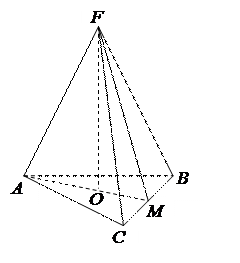
|
FABC – пирамида.
 : ∆АВС – правильный; : ∆АВС – правильный;
 : OF^(АВС); : OF^(АВС);
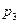 : О – центр описанной около ∆АВС окружности. : О – центр описанной около ∆АВС окружности.
|
После отведенного времени начинается опрос с ученика, составившего наименьшее количество заключений. Затем следующий ученик формулирует задачу, отличную от прозвучавшей. И так далее. Это позволяет опросить большее количество учащихся. Каждый из отвечающих должен доказать выдвинутое утверждение (устно или письменно).
Данный прием можно использовать на разных этапах – актуализации знаний; отработки знаний, умений и навыков; контролирующем этапе. Описанная организация решения системы задач может быть основой урока одной задачи. Все зависит от дидактических целей урока, трудности и сложности задачи, от подготовленности учащихся к данному виду работы.
Вопросы и задания
1. Исходя из условия задачи «А (1;-2), В (-1;0), С (5;4)» сформулируйте как можно больше заключений. Проанализируйте соответствующий параграф школьного учебника. Сколько задач с аналогичным условием предлагает автор? Сколько Вы составили? Решите составленные задачи.
2. Сформулируйте как можно больше положений о взаимном расположении прямых и плоскостей.
|
FABCD - пирамида
 : АВСD – прямоугольник; : АВСD – прямоугольник;
 : FB^(АВС). : FB^(АВС).
| |||
|
FABC – пирамида
 : FA=FB=FC; : FA=FB=FC;
 : FO^(ABC); : FO^(ABC);
 : АО=ОС. : АО=ОС.
|
        F
К В
А
С F
К В
А
С
|
FABC – пирамида
 : FK ^ AB, К : FK ^ AB, К 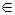 АВ; АВ;
 : FC ^ AB; : FC ^ AB;
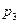 :двугранный угол FABC прямой. :двугранный угол FABC прямой.
|
           F
O D C
A
B
F
O D C
A
B
|
FABCD – пирамида
 : (FAB)^(FDC); : (FAB)^(FDC);
 : (FAB)^(АВС); : (FAB)^(АВС);
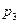 : (FDC)^(ABC). : (FDC)^(ABC).
|
            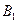  А1 D1
В С
A D
А1 D1
В С
A D
| ABCDA1B1C1D1 – призма
 : ABCD – прямоугольник : ABCD – прямоугольник
 : AA1B1B – прямоугольник. : AA1B1B – прямоугольник.
|
Опишите методику использования одной из геометрических ситуаций на одном из этапов урока по плану:
1) Название этапа.
2) Цель этапа.
3) Решение задачи.
4) Дидактические возможности задачи.
5) Организация процесса решения.
3. Пообдерите требование к условию задачи «Стороны основания прямоугольного параллелепипеда равны 3 и 4 см. Угол между диагональю параллелепипеда и плоскостью основания равен 600». Какие требования можно подобрать, если к условию задачи добавить «на боковом ребре параллелепипеда взята точка, которая делит это ребро в отношении 1:4»? Добавьте к условию исходной задачи еще одно любое предложение и подберите требование к вновь полученному условию.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1402; Нарушение авторских прав?; Мы поможем в написании вашей работы!
