КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод ключевой задачи
|
|
|
|
Метод составления системы задач, построенной по принципу – каждая задача системы использует результат решения (утверждение или метод) ключевой задачи будем называть методом ключевых задач.
| Задача №1 | Задача №2 | Задача №3 | ||

|  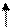
| |||
| Задача №1 | 
|  Ключевая задача Ключевая задача
| Задача №4 | |

|  
| |||
| Задача № … | Задача №6 | Задача №5 |
Существует две точки зрения на понятие ключевой задачи. Первая из них состоит в рассмотрении ключевой задачи как задачи-факта, результат решения которой может быть использован при решении каждой из задач системы. Зачастую такая ключевая задача оказывается дополнительной теоремой школьного курса. Приведем пример.
Ключевая задача. Если в трехгранном угле два плоских угла равны, то проекция их общего ребра на плоскость третьего плоского угла является его биссектрисой.
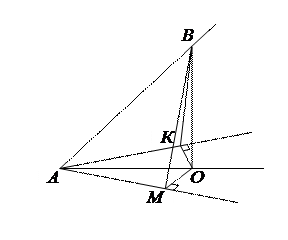
| Дано: 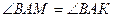 , , 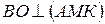 .
Доказать, что .
Доказать, что  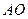 – биссектриса – биссектриса  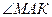 .
Доказательство.
Пусть .
Доказательство.
Пусть 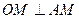 и и 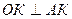 . Тогда по теореме о трех перпендикулярах . Тогда по теореме о трех перпендикулярах 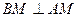 и и 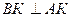 .
Треугольники .
Треугольники 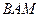 и и 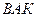 равны как прямоугольные по гипотенузе и острому углу. Следовательно, равны как прямоугольные по гипотенузе и острому углу. Следовательно, 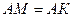 .
Треугольники .
Треугольники 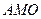 и и 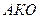 равны как прямоугольные по гипотенузе и катету. Следовательно, равны как прямоугольные по гипотенузе и катету. Следовательно, 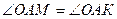 , а значит, , а значит,  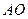 – биссектриса – биссектриса  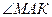 . .
|
Рассмотрим задачи системы:
1. Все грани параллелепипеда ромбы со стороной а и острым углом 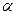 . Найдите объем параллелепипеда.
. Найдите объем параллелепипеда.
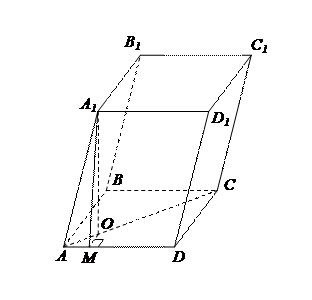
| Решение задачи начинается с анализа – что надо знать, чтобы найти объем параллелепипеда? Объем параллелепипеда равен произведению площади основания на высоту. Основанием данного параллелепипеда является ромб со стороной а и острым углом 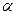 , следовательно, площадь основания можно найти по формуле , следовательно, площадь основания можно найти по формуле 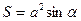 .
Чтобы найти высоту, надо ее построить. Где будет лежать основание перпендикуляра, проведенного, допустим, из вершины .
Чтобы найти высоту, надо ее построить. Где будет лежать основание перпендикуляра, проведенного, допустим, из вершины  к плоскости основания? Ответ на этот вопрос даст ключевая задача. к плоскости основания? Ответ на этот вопрос даст ключевая задача.
|
Далее решение задачи сводится к вычислению элементов параллелепипеда.
2. Основанием параллелепипеда служит прямоугольник со сторонами a и b. Боковое ребро параллелепипеда равно с, а углы между одним из боковых ребер и прилежащими к нему сторонами основания – 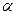 . Найдите объем параллелепипеда.
. Найдите объем параллелепипеда.
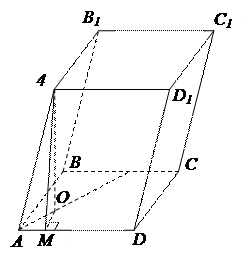
| Объем параллелепипеда можно вычислить по формуле 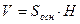 .
Основанием является прямоугольник со сторонами a и b, следовательно, .
Основанием является прямоугольник со сторонами a и b, следовательно, 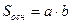 .
Проведем высоту параллелепипеда из вершины .
Проведем высоту параллелепипеда из вершины  . По ключевой задаче проекцией ребра . По ключевой задаче проекцией ребра 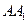 на плоскость основания на плоскость основания 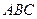 будет биссектриса угла будет биссектриса угла 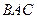 – – 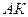 . .
|
Далее решение задачи сводится к решению прямоугольных треугольников.
3. В основании призмы лежит правильный треугольник со стороной а. Боковое ребро призмы равно b, а углы между одним из боковых ребер и прилежащими к нему сторонами основания – 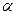 . Найдите объем призмы.
. Найдите объем призмы.
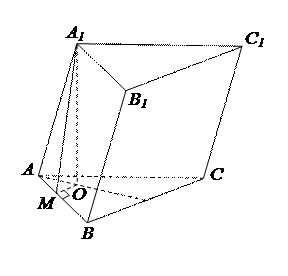
| 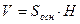 , , 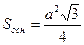 . .
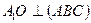 и и 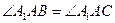 , следовательно, по ключевой задаче , следовательно, по ключевой задаче 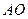 – биссектриса угла – биссектриса угла 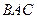 . .
|
4. В треугольной пирамиде все четыре грани – равные равнобедренные треугольники с основанием а и боковой стороной b. Найдите объем пирамиды.
Итак, в каждой задаче системы использовался факт, доказанный в ключевой задаче.
Вторая точка зрения состоит в рассмотрении ключевой задачи как задачи-метода. При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. В методической литературе выделяется четыре основных приема отбора ключевых задач.
Первый прием основан на умениях, которые должны быть сформированы у учеников после изучения темы. Для отбора задач учителю нужно просмотреть задачи по теме и соотнести их с умениями, которые планируется сформировать. Далее выбирается минимальное число задач, овладев умениями решать которые школьник сможет решить любую задачу из учебника по данной теме.
Второй прием – прием исключения и дополнения. Для его реализации нужно обратиться к задачам из учебника. Прочитать первую задачу – она кандидат на включение в список ключевых задач. Затем переходим к следующей задаче. Если она аналогична первой, то нужно решить, какую из них нужно оставить в списке ключевых. Если она существенно отличается от первой и не включается в нее, то эту задачу следует добавить к возможным кандидатам. Если вторая задача отличается от первой, но включает ее, то это означает, что первую задачу следует исключить, а вторую включить в число возможных ключевых задач. Далее нужно перейти к третьей задаче и повторить процедуру. Это необходимо проделать со всеми задачами учебника.
Третий прием выделения ключевых задач основан на методах решения задач по изучаемой теме. Выбор осуществляется в такой последовательности:
1) изучается набор задач в учебнике и дополнительных источниках;
2) задачи соотносятся с методами решения, отобранными для работы с учащимися;
3) выбирается 5-7 задач, при решении которых будут задействованы все отобранные учителем методы решения.
Четвертый прием выбора ключевых задач можно назвать комбинаторным. Для его реализации следует выделить объекты, которые фигурируют в задачах той или иной темы, рассмотреть возможные комбинации этих объектов, а потом для наиболее важных комбинаций подобрать задачу.
Покажем, как согласно первому из выделенных приемов можно выбрать ключевые задачи на тему «Показательная функция» по учебнику А.Г. Мордковича «Алгебра и начала анализа 10-11».
Для решения предложенных в пособии задач учащиеся должны уметь:
1) строить график показательной функции;
2) сравнивать значения степеней;
3) находить значения степенных выражений;
4) схематично изображать график показательной функции;
5) исследовать показательную функцию на монотонность;
6) находить наибольшее и наименьшее значение показательной функции на отрезке;
7) находить наибольшее и наименьшее значение показательной функции;
8) решать графически уравнения и неравенства;
9) находить область значений функции;
10) решать уравнения, используя монотонность функции.
Некоторые из перечисленных умений связаны или следуют из других умений. Так, учащиеся уже знают принцип графического решения уравнений и неравенств, и теперь, когда они познакомились с новой функцией, им достаточно научиться строить ее график, чтобы с его помощью решать уравнения и неравенства, т.е. восьмое умение следует из первого: 1) Þ 8). Анализируя, таким образом каждое из десяти умений, получим следующие зависимости: 1) Þ 8), 10); 5) Þ 2), 4), 6); 10 Þ 7).
Таким образом, получаем четыре ключевые задачи, требования которых заключаются в следующем: построить график показательной функции; найти значение выражения; исследовать показательную функцию на монотонность; найти область значения показательной функции. Вокруг этих задач могут быть сгруппированы все остальные задачи из учебника на тему «Показательная функция».
Вопросы и задания
1. Решите задачи:
1) Периметр равнобедренной трапеции ABCD равен 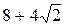 . Найдите углы трапеции, если AD=3ВС=6.
. Найдите углы трапеции, если AD=3ВС=6.
2) Чему равна диагональ квадрата со стороной 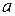 ?
?
3) ABCD – прямоугольник. АМ – биссектриса. АМ=  . М
. М 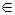 ВС. 3ВМ=МС. Найдите длины сторон прямоугольника.
ВС. 3ВМ=МС. Найдите длины сторон прямоугольника.
4) В треугольника АВС стороны АВ и ВС соответственно равны 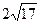 и 10 см,
и 10 см, 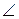 С=450. Найдите длину стороны АС.
С=450. Найдите длину стороны АС.
5) Чему равен периметр прямоугольной трапеции ABCD ( 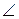 А=900), если АВ=ВС=2 см и
А=900), если АВ=ВС=2 см и 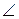 С=1350
С=1350
6) Основания равнобедренной трапеции со взаимно перпендикулярными диагоналями равны 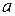 и
и 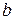 . Найдите диагонали и площадь трапеции.
. Найдите диагонали и площадь трапеции.
7) Найдите высоту ромба со стороной 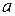 и углом в 1350.
и углом в 1350.
Сформулируйте задачу-факт, которая используется в каждой задаче данной системы. Установите связи между задачами. Составьте систему задач.
2. Решите задачи:
1) Сумма двух противоположенных сторон описанного четырехугольника равна 20 см. Найдите периметр этого четырехугольника.
2) В трапецию вписана окружность. Боковые стороны трапеции равны 5 см и 7 см. Найдите среднюю линию трапеции.
3) Докажите, что в любой ромб можно вписать окружность.
4) В равнобедренную трапецию вписана окружность. Основания трапеции равны 3 см и 7 см. Найдите боковую сторону трапеции.
5) Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб.
6) В равнобедренную трапецию с углом 300 вписана окружность. Средняя линия равна 12см. Найдите радиус вписанной в трапецию окружности.
7) Периметр описанного четырехугольника равен 10 см. Найдите сумму двух противоположенных сторон этого четырехугольника.
Сформулируйте задачу-факт, которая используется в каждой задаче данной системы. Установите связи между задачами. Составьте систему задач.
3. Решите задачи:
1) В основании пирамиды лежит прямоугольный треугольник с катетами, равными 12см и 5см. Все боковые грани наклонены к плоскости основания под углом 450. Найдите площадь боковой поверхности пирамиды.
2) В основании пирамиды лежит треугольник со сторонами 10, 10 и 12 см. Все апофемы равны по 5 см. Найдите объем пирамиды.
3) Основание пирамиды – прямоугольный треугольник с катетами 3 и 4 см. Все двугранные углы пирамиды при сторонах основания равны 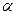 , причем
, причем 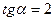 . Найдите объем пирамиды.
. Найдите объем пирамиды.
4) Основанием пирамиды является ромб со стороной 6 см. Каждый из двугранных углов при основании равен 450. Найдите объем пирамиды, если ее высота равна 1,5 см.
5) Основание пирамиды служит равнобедренная трапеция, основания которой равны 2 см и 8 см. Боковые грани наклонены к плоскости основания под углом 600. Найдите высоту пирамиды.
Сформулируйте задачу-факт, которая используется в каждой задаче данной системы. Установите связи между задачами. Составите систему задач.
4. Решите задачи:
1) Стороны треугольника 10, 10 и 12см. Найдите радиус вписанной в этот треугольник окружности.
2) Сумма двух противоположных сторон описанного четырехугольника равна 12 см, а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника.
3) Диагонали ромба равны 6 и 8 см. Найдите радиус вписанной окружности.
4) Сумма двух противоположных сторон описанного четырехугольника равно 10 см, а его площадь – 12 см2. Найдите радиус окружности, вписанной в этот четырехугольник.
5) Сторона правильного шестиугольника равна 2. Найдите его площадь.
6) Радиус вписанной в прямоугольный треугольник окружности равен 2см, а радиус описанной около него окружности равен 5 см. Найдите площадь треугольника.
7) Площадь равнобедренной трапеции, описанной около окружности радиуса 2 см, равна 24 см2. Найдите длину боковой стороны трапеции.
Сформулируйте задачу-факт, которая используется в каждой задаче данной системы. Установите связи между задачами. Составите систему задач.
5. Приведите один пример системы, составленной по методу ключевой задачи, из книги: Полонский В.Б., Рабинович Е.М., Якир М.С. Геометрия: Задачник к школьному курсу. – М.: АСТ-ПРЕСС: Магистр-S, 1998. – Гл. II.
| Системы задач | Фамилия студента |
| Параллельные прямые, пересекающие стороны угла | |
| Середины сторон четырехугольника | |
| Медиана, проведенная к гипотенузе | |
| Соотношения в прямоугольном треугольнике | |
| Вписанный угол | |
| Угол между касательной и хордой | |
| Величина угла, вершина которого лежит внутри (вне) окружности | |
Формула 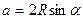
| |
| Свойства пересекающихся хорд | |
| Касательная и секущая, проведенные к окружности из одной точки | |
| Отношение площадей треугольников, имеющих общую высоту (основание) | |
| Отношение площадей подобных треугольников | |
| Площади треугольников, на которые четырехугольник разделен диагоналями | |
| Признак параллельности сторон четырехугольника | |
| Угол между биссектрисами внутренних односторонних и смежных углов | |
| Расстояние от вершины треугольника до точки касания вписанной окружности со стороной | |
| Свойства биссектрисы угла треугольника | |
| Второй признак подобия треугольников |
3.5 Метод целевой задачи
Метод целевой задачи предполагает выделение достаточно сложной задачи, решение которой разбивается на ряд простых задач.
Разбиение целевой задачи на элементарные осуществляется на основе анализа, что приводит к осознанию учащимися идеи доказательства.
Рассмотрим решение целевой задачи – доказать, что биссектрисы внутренних углов параллелограмма в пересечении образуют прямоугольник, диагональ которого равна разности смежных сторон параллелограмма.

Чтобы доказать, что OPLF – прямоугольник, достаточно утверждать, что OPLF – параллелограмм с прямым углом. Для этого достаточно доказать, что биссектрисы противоположных углов исходного параллелограмма параллельны, а биссектрисы смежных углов перпендикулярны.
Если удастся доказать, что РКСF – параллелограмм, то РF = КС, а КС = ВС–ВК. По условию задачи надо доказать, что КС = ВС–АВ. Следовательно, надо доказать, что АВ=ВК. Для этого достаточно утверждать, что треугольник АВК – равнобедренный.
Таким образом, решение целевой задачи представляет собой решение системы элементарных задач. Доказать, что: 1) биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой, 2) биссектрисы смежных углов параллелограмма пересекаются под прямым углом 3) биссектриса угла параллелограмма отсекает от него равнобедренный треугольник, 4) РКСF – параллелограмм и т.д.
Решение такой системы предполагает организацию коллективной деятельности – от работы каждой группы зависит решение целевой задачи.
Можно организовать решение целевой задачи, предваряя ее рассмотрением вспомогательных задач, назначение которых состоит в постепенном приближении к уровню сложности целевой задачи.
После решения целевой указываются задачи, развивающие ее.
| Вспомогательные задачи | |||||||
| № 1 | № 2 | № 3 | … | ||||

| |||||||
| Целевая задача | |||||||
| Задачи-обобщения | Задачи-следствия | ||||||
Построение системы данным методом предполагает решение двух основных задач: 1) вычленение задач – компонентов исходной целевой задачи и 2) выявление логических связей этих задач друг с другом.
Сконструировав таким образом систему, на каждом этапе имеем задачу, составляющую определенную «часть» исходной, менее сложную, чем исходная. Знание логической структуры задачи дает возможность построить каркас системы, но не систему в целом. Это объясняется тем, что на каждом новом шаге необходима не одна, а несколько задач, позволяющих создать индуктивную базу, достаточную для самостоятельного обобщения учащимися способа решения той или иной задачи. То есть целевая задача может предваряться несколькими системами задач.
Рассмотрим пример.
Целевая задача. Сторона правильного треугольника, вписанного в окружность, равна а. Найти площадь правильного шестиугольника, описанного около этой окружности и длину окружности.
Прежде чем решать эту задачу можно решить следующие системы вспомогательных задач.
Система 1.
1) Сторона правильного четырехугольника равна а. Найти его площадь.
2) Сторона правильного треугольника равна а. Найти его площадь.
3) Сторона правильного шестиугольника равна а, найти его площадь.
Система 2.
Пусть сторона правильного многоугольника равна а, радиусы описанной и вписанной в него окружности равны R и r.
1) Найти R и r для правильного треугольника, если a = 3.
2) Найти а и r для правильного четырехугольника, если R = 8.
3) Найти а и R для правильного шестиугольника, если r = 2.
Система 3.
Пусть An – сторона правильного n -угольника, описанного около окружности, an – сторона правильного n -угольника, вписанного в окружность.
1) Найти А 3, если а 4 = 2 см.
2) Найти а 4, если А 6 = 6 см.
3) Найти А 6, если а 3 = 4 см.
Данные три системы, составленные методом варьирования, предваряют решение более сложной целевой задачи.
Таким образом, при реализации указанного метода выделяется целевая достаточно сложная задача, решение которой предполагает применение основного ядра знаний учащихся и наиболее полно отражает сущность изучаемого материала. При первом подходе целевая задача рассматривается вместе с учащимися, во втором случае о предстоящей более сложной работе до определенного момента знает лишь учитель. После постановки целевой задачи, в результате ее анализа, учащиеся устанавливают связи между решенными задачами.
Целевая задача может быть задачей-обобщением предваряющих ее задач. Например, рассмотрев задачи: 1) В четырехугольнике ABCD проведена диагональ. Она разбивает его на два треугольника. Чему равна сумма внутренних углов четырехугольника? 2) Начертите в тетради пятиугольник и проведите все диагонали, выходящие из какой-нибудь его вершины. Сколько треугольников получилось? Чему равна сумма внутренних углов пятиугольника? Можно выполнить ее обобщение для n -угольника: Докажите, что сумма внутренних углов n -угольника равна 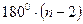 .
.
Вопросы и задания
3.6 «Снежный ком»
Метод «снежного кома» предполагает при решении каждой задачи системы использование результата решения предыдущей задачи.
Так как результатом решения задачи могут быть как доказанный факт об объекте, так и метод, реализованный в решенной задаче, то выделим две разновидности «снежного кома».
В первом случае идет использование доказанного утверждения. Например, рассмотрим систему задач:
1. 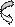 Доказать, что прямая, проходящая через вершину равнобокой трапеции параллельно ее боковой стороне, отсекает равнобедренный треугольник.
Доказать, что прямая, проходящая через вершину равнобокой трапеции параллельно ее боковой стороне, отсекает равнобедренный треугольник.
2. 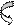 Доказать, что у равнобокой трапеции углы при основании равны.
Доказать, что у равнобокой трапеции углы при основании равны.
3. 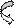 Доказать, что у равнобокой трапеции диагонали равны.
Доказать, что у равнобокой трапеции диагонали равны.
4. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба.
Решение.
| В равнобедренной трапеции ABCD прямая ВК параллельна стороне CD. Доказать, что треугольник АВК – равнобедренный. По определению КBCD – параллелограмм. Тогда, стороны ВК и CD равны. А по условию, стороны трапеции АB и CD равны. Следовательно, отрезки АВ и ВК равны и треугольник АВК – равнобедренный. |
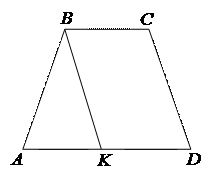 2. При решении второй задачи воспользуемся доказанным фактом. Для этого проведем прямую АК параллельную стороне CD равнобедренной трапеции ABCD.
2. При решении второй задачи воспользуемся доказанным фактом. Для этого проведем прямую АК параллельную стороне CD равнобедренной трапеции ABCD.
Треугольник АВК – равнобедренный. Тогда 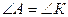 . А . А  как соответственные при параллельных прямых ВК и CD и секущей АD. Следовательно, как соответственные при параллельных прямых ВК и CD и секущей АD. Следовательно, 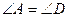 . .
|
3.
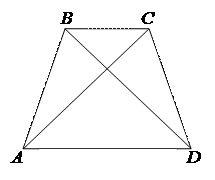
| Чтобы доказать, что у равнобедренной трапеции ABCD диагонали АС и BD равны, достаточно доказать равенство треугольников ABD и ACD. Для этого воспользуемся результатом решения предыдущей задачи, что 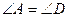 . Тогда треугольники ABD и ACD будут равны по двум сторонам и углу между ними. . Тогда треугольники ABD и ACD будут равны по двум сторонам и углу между ними.
|
4.
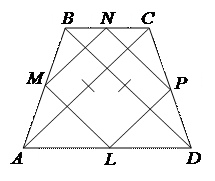
| MN и PL – средние линии треугольников ABC и ACD соответственно. Следовательно, они параллельны диагонали AC и равны ее половине. Тогда отрезки MN и PL – параллельны и равны. Следовательно, четырехугольник MNPL – параллелограмм. Чтобы доказать, что он является ромбом, достаточно показать равенство соседних сторон MN и NP. NP – средняя линия треугольника BCD. Тогда 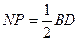 . По предыдущей задаче . По предыдущей задаче 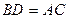 . Следовательно, . Следовательно, 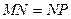 . .
|
Вторая разновидность рассматриваемого метода предполагает повторение операции предыдущей задачи. Наращивание «снежного кома» идет за счет добавления новой операции. Система задач, построенная таким методом, имеет следующую структуру. Для решения первой задачи необходимо выполнить всего одну операцию; решение второй задачи предполагает выполнение подобной операции, плюс еще одной операции, в следующей задаче системы, кроме двух ранее сделанных, выполняется новая третья операция и т.д., пока не дойдет до достаточно сложной задачи, решение которой предполагает выполнение большого количества операций.
| операция 1 | 
| операция 1 операция 2 | 
| операция 1 операция 2 операция 3 |
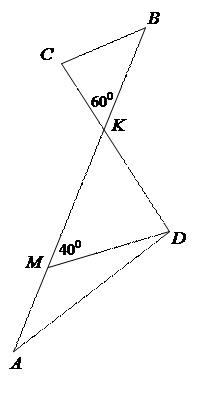
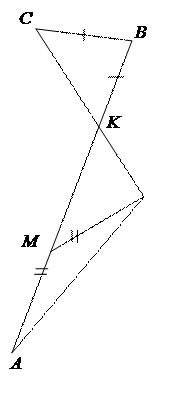
Например, по данным рисунка найдите величину угла CDM.
|
|
|
Возможность индивидуальной траектории при решении таких систем задач, возрастание уровня сложности и трудности задач обеспечивают дифференциацию обучения.
Вопросы и задания
1. Сформулируйте суть метода «снежного кома» при составлении систем задач.
2. Какую особенность имеет первая задача системы, составленной методом «снежного кома»?
3. В чем состоит существенной отличие метода «снежного кома» от метода целевой и ключевой задачи?
4. Решите задачу: «В прямоугольном треугольнике один из углов равен 300, а прилежащий к нему катет равен 6 см. Найдите гипотенузу треугольника». Добавьте к ней две-три задачи, чтобы получилась система, составленная методом «снежного кома».
5. Выберите любую задачу из школьного учебника по алгебре или по геометрии и, добавив к ней задачи, составьте систему методом «снежного кома».
4. Конструирование систем задач в зависимости
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 3959; Нарушение авторских прав?; Мы поможем в написании вашей работы!