От поставленных дидактических целей

В зависимости от поставленной дидактической цели целесообразно выбирать тот или иной метод конструирования системы задач.

Рассмотрим, как могут быть построены и использованы системы задач на этапе актуализации знаний, этапе создания мотивации, при изучении нового материала и при формировании умений и навыков.

1. Этап актуализации

От данного этапа зависит усвоение учащимися знаний, умений и навыков. Зачастую учителя в начале урока пытаются «освежить» опорные знания путем опроса учащихся. На самом же деле нельзя ограничиваться вопросами типа «что называется», «сформулируйте правило» и т.п. Ведь для того, чтобы хорошо усвоить материал, учащиеся должны не просто знать ранее изученную теорию, а уметь ее применять и работать с нею, иначе изучаемые на данном уроке знания будут формальными, неосознанными. Поэтому этап актуализации целесообразно проводить путем решения системы задач, требующей применения тех знаний, которые необходимо повторить. Эта система должна быть небольшой по размеру и ее решение не должно занимать много времени. После работы с системой у учащихся возникает четкое представление о необходимых в данный момент знаниях. Приведем пример.

Пусть на уроке будет изучаться теорема о суммах длин противоположных сторон описанного четырехугольника. Анализируя ее доказательство, замечаем, что в нем используется теорема о равенстве отрезков касательных, проведенных к окружности из одной точки. Учащиеся к этому моменту могут не помнить данной теоремы, поэтому целесообразно предложить им выполнить систему задач, составленную методом «снежного кома».

1) Из точки А к окружности с центром в точке О проведена касательная АВ, которая касается окружности в точке В. Найти величину угла АВО.

2) Из точки А к окружности проведены две касательные, касающиеся окружности в точках В и С. Определить вид АВС

3) Прямые АВ и АС касаются окружности в точках В и С. Угол ВАС равен 70. найти углы АВС и АСВ.

Актуализировать знания учащихся можно и путем варьирования элементов задачи. В этом случае появляется возможность повторения некоторого более объемного блока знаний. Пусть, например, на уроке необходимо, чтобы учащиеся вспомнили формулы вычисления площадей четырехугольников. Можно предложить им решить следующую систему задач.

Дан четырехугольник, площадь которого равна 36 см². Найти все его стороны, если этот четырехугольник является:

1) квадратом;

2) прямоугольником с диагональю 14 см;

3) ромбом, одна из диагоналей которого равна 10 см;

4) параллелограммом с высотой 6 см и острым углом 30⁰;

5) равнобочной трапецией с высотой 4 см и острым углом 60⁰.

Решая данную систему задач, учащиеся получают возможность повторить формулы площади основных видов четырехугольников.

2. Этап создания мотивации.

Очень трудно создать мотивацию словесно, более эффективными здесь окажутся задачи. В методической литературе довольно часто встречается утверждение, что мотивировать изучение материала нужно с помощью постановки проблемной задачи. Этот прием наиболее удачен, но и у него есть недостатки. Для того, чтобы учащиеся правильно восприняли предложенную задачу, необходимо осознание ими того, какими знаниями они уже обладают, а каких знаний еще не хватает. Здесь эффективно использование системы задач, составленной методом варьирования условия, когда решение первых задач системы не вызывает у них затруднений, а последняя задача дает четкое представление о необходимости получения новых знаний или умений.

В целом же, можно выделить два пути создания мотивации:

а) показ необходимости знания какой-то теоремы или правила для решения задач или доказательства новых утверждений;

б) показ необходимости знания какой-то теоремы или правила для решения практических задач.

Приведем несколько примеров.

Для мотивации изучения теорем синусов и косинусов при решении треугольников можно предложить следующую систему задач.

1) Дан прямоугольный треугольник с гипотенузой 3 см и острым углом 60. Найти остальные элементы треугольника.

2) Дан равнобедренный треугольник с основанием 8 см и углом при вершине 120. Найти остальные элементы треугольника.

3) Дан остроугольный треугольник, две стороны которого равны 5 и 8 см, а угол между ними равен 60. Найти остальные элементы треугольника.

Учащиеся без труда справляются с решением первой и второй задачи системы. После нескольких неудачных попыток решения третьей задачи учащиеся осознают, что они могут найти нужные элементы только у прямоугольных и равнобедренных треугольников, а для решения произвольных треугольников у них пока недостаточно знаний.

Приведем пример создания мотивации из необходимости решения практических задач.

Учащимся на уроке предстоит усвоить признак равенства треугольников по стороне и прилежащим к ней углам, причем признак равенства треугольников по двум сторонам и углу между ними уже известен учащимся.

Используем следующую систему задач:

1) Измерить на местности расстояние между точками А и В, между которыми нельзя пройти с мерной лентой.

2) Определить на местности расстояние между точками А и В, причем точка А недоступна.

При решении первой задачи учащиеся используют уже известный им признак равенства треугольников. Вторую задачу учащиеся решают вместе с учителем, а затем делают вывод, что в полученных при решении треугольниках имеется пара равных сторон и две пары углов, прилежащих к ним. Почему же эти треугольники равны? После этого можно приступать к изучению соответствующей теоремы.

3. Изучение нового материала

Урок усвоения новых знаний включает в себя четыре основных этапа:

- актуализация опорных знаний;

- создание мотивации;

- восприятие и осознание нового материала;

- обобщение и систематизация знаний.

При ознакомлении с новым материалом целесообразно использовать систему задач, решение которой приводит к идее доказательства теоремы либо к ознакомлению с существенными признаками понятий, а также задачи, в процессе выполнения которых учащиеся самостоятельно «открывают» и формулируют новые теоремы. Благодаря своей структуре, такая система задач поможет учащимся шаг за шагом проследить все связи, закономерности и особенности материала, и это обеспечит осознанность усвоения ими новых знаний.

Пусть, например, изучается тема о пропорциональных отрезках в прямоугольном треугольнике. Учащимся могут без труда сами вывести готовые формулы, если предложить им решить следующую систему задач.

1) В прямоугольном треугольнике АВС с прямым углом С проведена высота СD. Доказать, что треугольники АСD и СВD подобны исходному треугольнику.

2) Доказать, что треугольник АСD подобен треугольнику СВD.

3) Вывести отношения, выражающие высоту через отрезки, на которые гипотенуза делится данной высотой, и катеты через гипотенузу и их проекции на нее.

После решения данной системы, учащиеся не только поймут, откуда взялись эти отношения, но и в случае их забывания, они смогут быстро вывести их заново.

4. Формирование умений и навыков.

Урок данного типа имеет следующую структуру:

- актуализация опорных знаний;

- создание мотивации;

- изучение нового материала;

- применение учащимися знаний в стандартных условиях;

- перенос знаний и навыков в новые условия.

Подбор систем задач к первым трем этапам был рассмотрен выше, и он ничем не отличается от аналогичной процедуры подготовки урока усвоения новых знаний. Основное назначение системы задач на четвертом этапе – довести знания до полного усвоения и применения их в условиях, когда знания еще не достаточно устойчивы. Здесь необходимо добиться от учащихся сформированности нужных умений и навыков и готовности перейти к более сложным задачам.

Учащиеся на уроке познакомились со свойством пересекающихся хорд. Тогда это свойство может рассматриваться как ключевая задача и далее можно предложить учащимся систему задач, составленную этим методом.

1) Вокруг треугольника АВС описана окружность. Через точку К этой окружности и точку В проведена хорда, пересекающая сторону АС в ее середине – точке М, причем 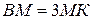. Найдите отношение .

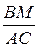2) Дана точка Р, удаленная на 7 см от центра окружности радиуса 11 см. Через эту точку проведена хорда длиной 18 см. Каковы длины отрезков, на которые делится хорда точкой Р?

3) Середина D полуокружности соединена с концами диаметра АС. Хорда ВЕ параллельна АС и делится хордами АD и СD на три равные части. М – точка пересечения хорд АD и ВЕ. Найдите длину отрезка DМ, если .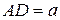

4) Сторона АВ треугольника АВС является хордой некоторой окружности. Стороны АС и ВС лежат внутри окружности, продолжение АС пересекает окружность в точке D, а продолжение ВС – в точке Е. Найдите радиус окружности, если АВ=АС=СD= 2 и СЕ= 2.

5) В окружность вписан равнобедренный треугольник АВС, , 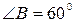. Средняя линия треугольника продолжена до пересечения с окружностью в точках D и Е. Найти отношение площадей треугольников АВС и DВЕ.

Первые три задачи не должны вызвать затруднений у учащихся, и они отвечают требованиям этапа применения знаний в стандартных условиях. Последние две задачи более трудны и могут служить пятым этапом урока формирования умений и навыков.

Таким образом, в зависимости от поставленных дидактических целей в учебном процессе могут быть использованы системы задач, построенные различными методами.

Вопросы и задания

Система 1.

1) В прямоугольном треугольнике АВС с прямым углом С проведена высота CD. Докажите, что треугольники ACD и CBD подобны треугольнику АВС.

2) Докажите, что треугольник ACD подобен треугольнику CBD.

3) Выведите отношения, выражающие высоту прямоугольного треугольника, проведенную к гипотенузе, через отрезки, на которые она делится этой высотой, и катеты через гипотенузу и их проекции на нее.

Система 4.

1) В треугольнике АВС известны длины сторон, равные 41, 51 и 58 см. Вычислите площадь треугольника.

2) Найдите площадь треугольника, если две его стороны равны 1 см и 15 см, а медиана, проведенная к третьей стороне, равна 2 см.

3) Длины двух сторон треугольника равны 27 см и 29 см. Длина медианы, проведенной к третьей стороне, равна 26 см. Найти высоту треугольника, проведенную к стороне длиной 27 см.

4) Две стороны треугольника равны 1 см и 13 см, медиана, проведенная к третьей стороне, равна 2 см. Найти длины отрезков, на которые высота разбивает сторону длиной 1 см.

Система 5.

1) Докажите, что сумма смежных углов равна 180°.

2) Найдите угол, смежный с углом 47°.

3) Найдите смежные углы, если одни из них на 20° больше другого.

4) Найдите смежные углы, если их градусные меры относятся как 2: 3.

Система 6.

Пусть A_n – сторона правильного n -угольника, описанного около окружности; а_n – сторона правильного n -угольника, вписанного в эту окружность. Найдите: 1) A₃, если а₄ = 2 см. 2) а₄, если А₆ = 6 см. 3) A₆, если а₃ =4 см.

5. Итоговый тест

1. Можно ли любой набор задач назвать системой?

а) да б) нет

2. Является ли метод аналогии методом конструирования систем задач?

а) да б) нет

3. Верно ли, что правила построения систем задач включают в себя правила отбора задач и правила их упорядочивания?

а) да б) нет

4. Может ли одна и та же задача быть адекватной для одних учащихся класса и неадекватной для других?

а) да б) нет

5. Верно ли, что в системе должно быть не больше трех однотипных задач?

а) да б) нет

6. Верно ли, что можно варьировать только условие и требование задачи?

а) да б) нет

7. Верно ли, что обобщение и конкретизация являются приемами варьирования задачи?

а) да б) нет

8. Является ли правило усложнения правилом упорядочивания задач системы?

а) да б) нет

9. Верно ли, что в качестве ключевой задачи может быть выбрана любая задача по изучаемому материалу?

а) да б) нет

10. Целесообразно ли на этапе актуализации знаний применять систему, составленную методов варьирования задачи?

а) да б) нет

11. Что из перечисленного является требованием к системе задач?

а) простота

б) объемность

в) иерархичность

12. Какие из перечисленных методов являются методами конструирования систем задач?

а) метод ключевой задачи

б) метод неполной задачи

в) аналитический метод

г) метод варьирования

13. Укажите, какие правила способствуют удовлетворению приведенных требований к системе задач?

а) правило доступности 1) целевая достаточность

б) правило разнообразия 2) адекватность

в) правило учета целей 3) полнота

14. Какие из приведенных уравнений являются доступными для учащихся 9 класса?

а)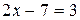

б)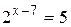

в)

15. Что из перечисленного является приемом варьирования задачи?

а) прием противоположных задач

б) прием аналогии

в) прием синтезирования задачи

16. Какие из перечисленных видов задач относятся к нестандартизированным?

а) неопределенные

б) противоречивые

в) интегрированные

г) провоцирующие

17. Какие из перечисленных правил являются правилами отбора задач в систему?

а) простоты

б) разнообразия

в) ситуативности

18. Сколько вспомогательных задач должно предварять решение целевой задачи?

а) не более двух

б) не более трех

в) в зависимости от ситуации

19. Перечислите требования к содержанию систем задач

1. … 2. …

20. Перечислите методы конструирования систем задач

1. … 2. … 3. … 4. …

21. Перечислите правила упорядочивания задач

1. … 2. … 3. …

22. Перечислите этапы конструирования системы задач

1. … 2. … 3. … 4. …

23. В чем состоит требование иерархичности к системе задач?

24. Какие действия необходимо совершить на структурирующем этапе конструирования систем задач?

25. К какому методу конструирования систем задач относится решение одной задачи разными способами?

26. В чем состоит требование целевой достаточности системы задач?

27. В чем состоит метод целевой задачи?

28. В чем состоит правило структурности построения системы задач?

29. В чем состоит суть метода варьирования задачи?

30. В чем состоит суть приема составления обратных задач?

31. Опишите алгоритм преобразования стандартной задачи в вариативную.

32. Какие два подхода существуют к определению ключевой задачи?

33. Какие методы конструирования систем задач наиболее целесообразно использовать при подготовке к уроку обобщения и систематизации знаний?

34. Какие действия необходимо совершить над стандартизированной задачей, чтобы получить из нее преопределенную?

35. Перечислите виды нестандартизированных задач.

36. Какая задача называется вариативной?

37. Опишите, как на практике может быть учтен принцип соответствия времени?

38. Как при конструировании системы задач добиться выполнения всех требований, предъявляемых к ее содержанию? Возможны ли ситуации, когда некоторые из этих требований могут не учитываться? Ответ обоснуйте.

39. На каких этапах урока и почему лучше использовать метод целевой задачи при конструировании системы?

40. Как, используя правила отбора задач в систему, добиться выполнения требований к ее содержанию? Укажите, какие из правил оказывают непосредственное влияние на соблюдение того или иного требования.

41. Какая существует связь между отборочным и структурирующим этапами конструирования систем задач? Могут ли эти этапы пересекаться? Ответ обоснуйте.

42. Как можно, варьируя условие задачи, добиться от учащихся открытия какого-либо математического факта?

43. При проведении каких видов урока, и на каких этапах целесообразно предлагать учащимся задачи с несформированным требованием? Ответ обоснуйте.

44. Опишите четыре основных приема отбора ключевых задач. Существует ли какая-либо связь между выбором приема для каждого конкретного урока математики. Ответ обоснуйте.

45. Опишите методику использования на уроках математики задач с несформированным требованием. Укажите, на каких этапах урока их лучше всего использовать.

Данный тест рассчитан на 80 минут, вопросы распределены по мере нарастания сложности: 18 вопросов – первого уровня, 18 – второго и 9 – третьего уровня сложности.

6. Примерные темы для рефератов, курсовых,

Дата добавления: 2014-12-16