Вариативные задачи

Постановка проблемы. Анализ школьных учебников геометрии выявил задачи, которые имеют неоднозначное решение, а в условии или требовании задачи нет прямого указания на возможные варианты решений. Правильность решения таких задач зависит от подготовки учителя, от наличия у него умения «видеть» задачу в различных вариантах. У учащихся, в случае получения различных ответов, возникает сомнение в правильности постановки задачи. И со всеми вопросами они вновь обращаются к учителю, который зачастую не готов дать исчерпывающий ответ. Лишь хорошо подготовленный преподаватель приходит к правильному решению такого рода задач. Это задачи, допускающие неоднозначное решение, – вариативные задачи. Они не выделены в особый класс, поэтому очень часто происходит потеря решений. Однако именно вариативные задачи наиболее значимы для развития критичности мышления, комбинаторных способностей учащихся, создают ситуации побуждения к более вдумчивому анализу заложенной в задаче информации и ее структурированию. Задачи указанного типа приближены к жизненно-практическим условиям, так как любая жизненная ситуация как правило имеет несколько вариантов исхода. Вариативные задачи создают условия для выработки собственного взгляда на ситуацию и переносят акцент с самого процесса усвоения знаний на их осмысление, наполнение личностным смыслом, что, в свою очередь, обеспечивает более эффективное усвоение знаний.

В методической литературе задачам выделенного типа не уделяется должного внимания. Феномен вариативных задач изучен недостаточно. В учебно-методической литературе встречаются примеры многовариантных задач. Но на сегодняшний день не разработаны рекомендации, эвристики, позволяющие застраховать учащихся от неполных решений. Использование большого количества вариативных задач в учебниках нового поколения только доказывает необходимость изучения методики их решения.

Понятие вариативной задачи. В большем числе случаев геометрические задачи школьных учебников имеют однозначное решение. В этом мы сами убедились, проанализировав учебники геометрии под редакцией А.В. Погорелова и Л.С. Атанасяна. Из общей массы задач всего порядка десятка имеют интересующую нас характеристику – несколько вариантов решения, влекущих за собой различные ответы. Именно такие задачи мы и будем называть вариативными.

Под вариативной будем понимать задачу, у которой формулировка не допускает точного установления взаимного расположения объектов условия или требования.

Отличие вариативной задачи от стандартной можно представить схематично.

Стандартная задача Вариативная задача

решения решения

Решить вариативную задачу значит рассмотреть все возможные варианты расположения объектов. Например, в задаче: «На книжной полке стоит двухтомник. Толщина страницы составляет 0,05 мм, а толщина обложки – 1 мм. В первом томе 320 страниц, а во втором – 400. Жучок прогрыз две книги от первой страницы первого тома до последней страницы второго. Какое расстояние он при этом прополз?» возможны два решения в зависимости от того, как стоят книги.

Не рассматривая различные варианты расположения искомой фигуры невозможно решить задачу: «Постройте квадрат по двум данным вершинам А(0,0); К(-2,4)». Чем будет являться отрезок АК – диагональю или стороной искомого квадрата? Отвечая на подобные вопросы, ученики учатся рассматривать все возможные варианты заданной в задаче ситуации, то есть приучаются к "полноте дизъюнкции".

Полонский В.Б., Рабинович Е.М., Якир М.С. выделяют условия, ведущие к неоднозначной трактовке задачи:

1. Условие задачи не определяет взаимное расположение точек и фигур:

а) точка или принадлежит отрезку АВ, или ему не принадлежит, но лежит на прямой АВ; б) точки лежат или в одной полуплоскости относительно заданной прямой, или в разных (то же с полупространством); в) различные расположения центра описанной окружности или ортоцентра треугольника в зависимости от вида треугольника.

2. В условии задачи фигурируют две касающихся окружности, но не указан способ касания: внешний или внутренний. В задаче даны две точки, делящие окружность на две дуги, кроме того, известно, что некоторая прямая касается окружности, но не указано на какой из двух дуг лежит точка касания.

3. В задаче фигурируют объекты, которым приписываются определенные свойства, но не указан порядок соответствия между множеством объектов и множеством их свойств: а) сказано, что АВС – равнобедренный треугольник, но не сказано, какие пары сторон равны; б) точка М делит отрезок АВ на отрезки длинной а и b, при этом не уточняется, какой из них равен а, а какой b; в) известно, что угол между пересекающимися прямыми АВ и CD равен a, однако, не указано, который из углов – AMD или АМС (М – точка пересечения прямых) – острый.

Возможны и другие причины возникновения вариативности. Например, при решении задачи: «Постройте треугольник по двум сторонам и углу, прилежащему к одной из них» можем получить два треугольника, удовлетворяющих требованию задачи.

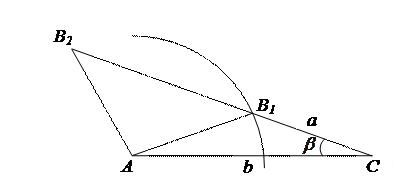
Ни одно из условий, выделенных авторами книги //, не объясняет два ответа в данной задаче. Кроме того, не выделены особенности возникновения вариативности в алгебраических зада-

чах. (Например, в задачах на прогрессию очень часто получаются два ответа.)

Конструирование вариативных задач. Получить вариативную задачу можно из стандартной задачи учебника. Для этого нужно разбить условие и требование задачи на объекты и их характеристики, убрать некоторые из них и проверить на корректность.

Дата добавления: 2014-12-16