КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обобщение и конкретизация задач 1 страница
|
|
|
|
Кеплер
Задачи по аналогии
…Я больше всего дорожу Аналогиями, моими самыми верными учителями. Они знают все секреты Природы, и ими меньше всего следует пренебрегать в Геометрии.
При решении задач субъект (осознанно или нет) пытается установить связь между предложенной задачей и накопленным им опытом. Изучая отдельные элементы задачи, анализируя отношения между ними, он может найти среди них такой, который привлечет полезные знания, приобретенные ранее. Мобилизация элементов, имеющих отношение к задаче, зачастую и начинается с распознавания некоторого элемента, содержащегося в задаче, и с вспоминания связанных с ним и уже знакомых других элементов. Многие школьники начинают действовать с другого конца: не с анализа данных, относящихся к задаче, а с обращения к ранее полученным знаниям до тех пор, пока не найдется какой-нибудь знакомый элемент, метод, способ решения, который окажется или покажется полезным для данной задачи.
Во всех этих случаях субъект действует по аналогии. Сразу определимся, что предпочтителен первый путь через анализ условия задачи. Второй способ использования аналогии чаще всего сводится к бездумному копированию решения «внешне» аналогичной задачи.
При составлении задач также можно действовать по аналогии, причем в большинстве случаев составитель и не сможет абстрагироваться от ранее накопленных знаний и составить оригинальную, не похожую на встречаемые в учебной литературе задачи. Поэтому один из приемов, которые мы будем применять при обучении составлению задач - действие по аналогии.
Аналогия – один из видов традуктивного умозаключения (лат. Traductio – перемещение). Как метод исследования, традукция заключается в том, что установив сходство двух объектов в некотором отношении, делают вывод о сходстве тех же объектов в другом отношении. Аналогия – сходство предметов в каких-либо свойствах, признаках, отношениях, причем, таких предметов, которые в целом различны (Кондаков Н.И. Логический словарь-справочник. – М.: Наука, – 1975.). При умозаключении по аналогии знание, полученное из рассуждений о каком-либо объекте, переносится на другой, менее изученный объект.
Схема умозаключения по аналогии:
1 шаг. Предмет А обладает свойствами a, b, c, x.
2 шаг. Предмет В обладает свойствами a, b, c.
Вывод. Вероятно, предмет В обладает и свойством x.
Суждения, полученные по аналогии, носят вероятный характер и подлежат исследованию. Они являются источником научных гипотез и играют важную роль в научных открытиях. “Аналогия лишь открывает путь исследования и не имеет доказательной силы” (Эрдниев П.М.).
Как положительный эвристический фактор аналогия может оказать помощь в трех направлениях:
1. Она может быть применена для того, чтобы навести учащихся на отыскание нового для них предложения и помочь сформулировать его.
2. Она может дать указание о выборе метода и приема доказательства предложения.
3. Она может оказать помощь в отыскании путей решения задач.
Подчеркивая значимость умения рассуждать по аналогии в математике, следует отметить, что:
· это умение развивает умственные, познавательные способности учащихся, развивает творчество, формирует вкус к поисково-исследовательской деятельности;
· переносимость математических методов доказательств с помощью аналогии на другие науки (химия, физика, логика и др.) дает широкое применение умению доказывать;
· аналогия школьных методов доказательств с научными методами познания, лежащими в основе научных методов исследования, дает дальнейшее развитие умению доказывать.
Выделим дидактическую эффективность использования аналогии при обучении математике:
1) Использование аналогии при открытии математических фактов делает учащихся «соавторами» математической теории, знакомит учеников с мощным методом познания действительности.
2) Аналогия интенсифицирует (ускоряет) процесс изучения математики, позволяя изучать сходные свойства различных математических объектов. Примером является совместное изучение планиметрических и стереометрических фигур. (Диагонали прямоугольника равны. Диагонали прямоугольного параллелепипеда равны. У квадрата его измерения равны. У куба его измерения равны.).
3) Аналогия является одним из способов открытия доказательства математических утверждений. Использование «неправильных» аналогий формирует у учащихся потребность в доказательстве.
Рассмотрим некоторые вопросы методики использования аналогии при обучении математике.
Почву для применения аналогии подготавливает сравнение. Задания на сравнение должны присутствовать на уроках постоянно. Например, при изучении нового понятия необходимы задания на установление сходства и различия его с раннее изученными понятиями. Устные упражнения могут содержать вопросы следующего характера: в чем схожесть и в чем различие параллелограмма и прямоугольника, прямоугольника и ромба, ромба и квадрата, квадрата и куба, куба и параллелепипеда?
Интересное для учащихся задание на сравнение может быть построено при помощи методики «Найди лишнее»: учитель зачитывает по четыре слова, из которых три объединены общим родовым понятием, а одно к такому понятию не относится или относится в меньшей мере. Учащиеся должны определить это слово и записать в тетради. На запись дается 10 секунд.
1. Цилиндр, шар, куб, конус.
2. Прямоугольный параллелепипед, куб, тетраэдр, наклонный параллелепипед.
3. Прямоугольник, треугольник, ромб, квадрат.
4. Цилиндр, куб, многоугольник, шар.
5. Равнобедренный, прямоугольный, остроугольный, тупоугольный треугольник.
6. Пирамида, параллелепипед, куб, шар.
7. Треугольник, круг, трапеция, квадрат.
8. Ромб, трапеция, квадрат, прямоугольник.
9. Октаэдр, тетраэдр, икосаэдр, параллелограмм.
10. Параллелограмм, треугольник, куб, окружность.
11. Дуга, сегмент, окружность, прямая.
Причем в последних примерах могут быть разные варианты ответов. В десятом «лишним» может быть или куб или окружность, в одиннадцатом – или сегмент или прямая. Все зависит от выбора родового понятия. Неоднозначности в рассуждениях, ответах тоже надо учить. Поэтому такие задания необходимо включать в процесс обучения с последующим обсуждением результатов.
При ознакомлении учащихся с гомотетией, центральной и осевой симметрией можно дать следующие упражнения, выполняя которые учащиеся приучаются устанавливать сходства и различия изучаемых понятий //:
1. Прямые BO и AA1 пересекаются в точке О. Точки А и А1 симметричны относительно оси ВО. Симметричны ли точки А и А1 относительно точки О?
2. Составьте обратное утверждение. Прямые BO и AA1 пересекаются в точке О. Точки А и А1 симметричны относительно точки О. Симметричны ли точки А и А1 относительно оси ВО?
3. Точка С гомотетична точке В относительно центра О с коэффициентом k = 2. Будут ли точки О и С симметричны относительно точки В?
4. МО – медиана треугольника АМК, АМ = МК. Верно ли, что точки А и К симметричны относительно оси ОМ? Относительно точки О? ОМ – ось симметрии треугольника? О – центр симметрии треугольника?
Кроме заданий на нахождение сходства и различия геометрических объектов и их элементов внимание следует уделять выделению соответственных элементов из аналогичных теорем и задач, то есть учитель должен предлагать учащимся системы задач, преследуя цель – показать их “сходство”.
Например, рассмотрим две пары задач из учебника А.В. Погорелова (8 изд. М.: Просвещение, 1989г.).
| Докажите, что у равнобедренного треугольника биссектрисы, проведенные из вершин при основании равны (№19(1)) | Докажите, что у равнобедренного треугольника медианы, проведенные из вершин при основании равны (№19(2)) |
| Докажите равенство треугольников по двум сторонам и медиане, исходящим из одной вершины. (№38). | Докажите равенство треугольников по медиане и углам, на которые медиана разбивает угол треугольника. (№40). |
Для биссектрисы в задаче №19(1) соответственным элементом в задаче №19(2) является медиана. В задачах второй пары соответственными элементами оказались: две стороны, исходящие из одной вершины (№38) и два угла, на которые разбивает медиана угол треугольника (№40). Решение задач нужно вести параллельно, подчеркивая, что каждый шаг одного из них можно перенести на другой, переменив их к соответственным элементам.
Важно учить школьников видеть не только аналогию геометрических объектов и их элементов, но и аналогию свойств, аналогию отношений между объектами. Выделим некоторые виды отношений между геометрическими объектами:
· “Часть – целое” (отрезок – прямая, луч – прямая, …).
· “Объект – ближайший род” (сторона – отрезок, тетраэдр – многогранник,…).
· “Плоскость – пространство” (точка – прямая, вершина – ребро, …).
· “Объект – его элемент” (параллелограмм – сторона, квадрат – диагональ,…).
· “Объект – геометрическая величина” (треугольник – площадь, куб – объем,…),
· “Геометрическая величина – единица измерения” (площадь – м2, объем – м3,…).
Соответствующие задания могут быть следующими.
1. Замените знак “?” геометрическим объектом из списка.
Диаметр: Радиус = Окружность:?
а) отрезок; б) точка; в) дуга; г) линия; д) луч.
Точка: Прямая =?: Пространство
а) отрезок; б) плоскость; в) прямая; г) луч; д) точка.
2. Заполните пустые ячейки таблицы.
| Линейный угол | Двугранный угол | Пространство | ||
| Лучи | Многоугольник | Плоскость |
3. Укажите в списке пары объектов, находящиеся в отношении, аналогичном отношению пары “сторона – отрезок”.
а) перпендикуляр – отрезок; б) треугольник – точка; в) угол – фигура;
г) тетраэдр – грань; д) параллелепипед – многогранник.
4. Составьте пары (укажите стрелки соответствия), находящиеся в том же отношении, что и пара “сторона – грань”.
Треугольник Прямая
Точка Тетраэдр
Угол Ребро
Вершина Параллелепипед
5. Выберите из предложенного списка геометрические объекты, которые находятся с объектом “треугольник” в том же отношении, что и объект “сторона”.
Постепенно задания на применение метода аналогии должны усложняться, и учащиеся вскоре смогут самостоятельно не только решить предложенное задание, но и сами составить и доказать геометрическое утверждение, аналогичное данному.
Действия по построению утверждения, аналогичного данному и доказательства, аналогичного данному целесообразно выделить вместе с учащимися:
1. Осмыслить исходное утверждение
2. Выделить в нем объекты, свойства, отношения между ними.
3. Заменить объекты на им аналогичные либо оставить без изменения.
4. Сохранить свойства.
5. Сохранить отношения (равенства или неравенства).
6. Изменить числовые отношения либо оставить без изменения.
7. Сформулировать полученное утверждение.
Действия по нахождению доказательства, аналогичного данному:
1. Разбить исходное доказательство на этапы.
2. Сохранить последовательность этапов.
3. Каждый этап либо повторить, либо изменить с учетом аналогии объектов и их свойств.
После определения выше указанных действий учащимся можно предложить следующее задание: Составить задачу, аналогичную данной, решить обе задачи.
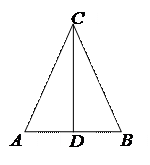
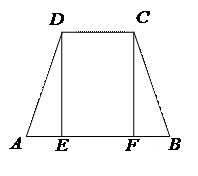
В равнобедренном треугольнике углы при основании равны.
1. Проведем высоту CD. 2. Треугольники ACD и BC D равны. | В равнобедренной трапеции углы при основании равны.
1. Проведем высоты DE и CF. 2. Треугольники ADE и BCF равны. |
Приведем примеры стереометрических задач, аналогичных планиметрическим.
Планиметрическая задача
В равнобедренный треугольник МНК вписана окружность. Доказать, что радиус окружности равен 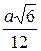 , если известно, что , если известно, что 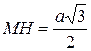 , , 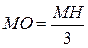 . .
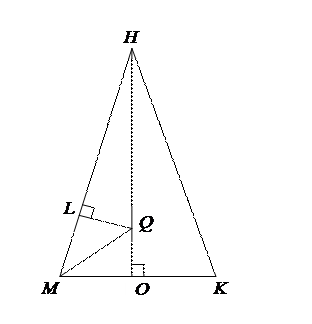 1. Q=HOÇMQ, MQ – биссектриса угла НМО, НО^МО.
2. DHLQ подобен DНОМ:
1. Q=HOÇMQ, MQ – биссектриса угла НМО, НО^МО.
2. DHLQ подобен DНОМ:
  ; ;  .
3. .
3. 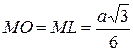 , , 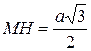 Þ Þ 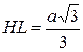 , , 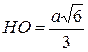 .
4. Имеем .
4. Имеем 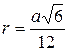 . .
| Стереометрическая задача
В правильную треугольную пирамиду, у которой все ребра равны а, вписан шар. Доказать, что радиус шара 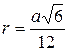 . .
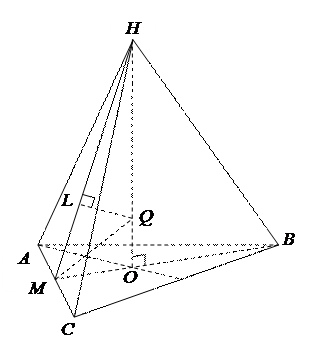 1. Q=HOÇMQ, MQ – биссектриса угла НМВ, НО^(АВС).
2. DHLQ подобен DНОМ:
1. Q=HOÇMQ, MQ – биссектриса угла НМВ, НО^(АВС).
2. DHLQ подобен DНОМ:
 ; ;  .
3. .
3. 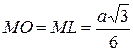 , , 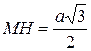 Þ Þ 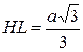 , , 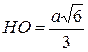 .
4. Имеем .
4. Имеем 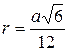 . .
|
Видно, что не только формулировки этих двух задач, но и этапы доказательства аналогичны.
Типичные вопросы учителя при решении задач методом аналогии:
§ Не решали ли вы подобные задачи?
§ Какими приемами решалась подобная задача?
§ В чем отличие новой задачи от раннее решенной?
§ Нельзя ли свести доказательство новой задачи к доказательству раннее решенной?
Лецко В.А. // предостерегает о постановке этих вопросов на ранней стадии решения задачи. По его мнению, попытка побыстрее найти аналогичную уже решенную задачу чаще всего приводит к обнаружению задач, аналогичных данной лишь по признаку внешнего сходства. Основным приемом решения задачи по аналогии должен быть не переход от ранее разобранной аналогичной задачи к данной, а от данной задаче к аналогичной. Именно такой подход обеспечивает выявление содержательных аналогий на уровне идей и механизмов решения, а не внешнего сходства условий и обозначений.
Надо помнить, что не во всех случаях рассуждения по аналогии оказываются верными. Примеры ложных аналогий:
1. Через точку на прямой в пространстве можно провести только один перпендикуляр к этой прямой.
2. Две прямые в пространстве, перпендикулярные к одной и той же третьей прямой, параллельны.
3. Высоты в тетраэдре пересекаются в одной точке.
Важно, чтобы учащиеся в поиске правильных ответов сами могли находить ошибочность возникающих в этом процессе предложений.
В преподавании полезно сформировать и постепенно из урока в урок пополнять список аналогичных геометрических объектов и пар аналогичных задач. Пары аналогичных задач по разным темам геометрии приведены в статье Кочагина В.В. Список аналогичных геометрических задач. / Математика в школе, 1999. – № 1. – с.69-70.
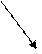
Приведем пример построения системы задач по теме «Нахождение производных функций». Учащиеся должны сначала установить отношения между имеющимися данными по типу «функция» 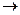 «ее производная», а затем заполнить пропуски в карточках по аналогии установленным связям.
«ее производная», а затем заполнить пропуски в карточках по аналогии установленным связям.
|  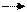
| 
| 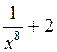
|  
| 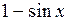
| |
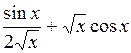
| 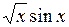
| 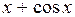
| 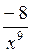
| |||

| ? | 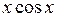
| ? | |||
| ? | 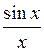
| 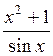
| ? |
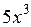
| 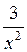
| 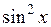
|  
| 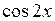
| ||
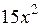
| ? | 
| 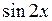
| |||
 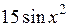 
| 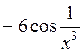
| 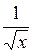
| 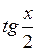
| |||
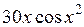
| ? | ? | ? |

|  
| 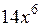
| 
|  
| 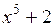
| |
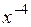
| 
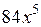
| 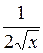
| ? | |||

| 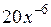
| ? | 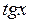
| |||

|  ? ?
| 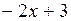
| ? | |||

| ? | 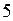
| ? | |||
| ? | ? |  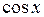
| 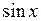
|
Простое применение аналогии позволяет получить задачу, однопорядковую с данной. От него следует отличать составление задачи обобщением, когда новая задача оказывается в том или ином отношении сложнее исходной. Описание роли, места, методики использования обобщения задач в процессе обучения математики и при конструировании систем задач – цель следующего параграфа.
Вопросы и задания
1. Законспектируйте материал о роли и месте аналогии при обучении математике:
а) Эрдниев П.М. Аналогия в математике. – М.: Знание, 1970.
б) Далингер В.А. Об аналогиях в планиметрии и стереометрии / Математика в школе, 1995. – № 6.
в) Саранцев Г.И., Лунина Л.С. Обучение методу аналогии / Математика в школе, 1989. – № 4.
2. Диагональ параллелограмма разбивает его на два равновеликих треугольника. Верно ли, что если каждая диагональ четырехугольника разбивает его на два равновеликих треугольника, то этот четырехугольник является параллелограммом?
3. Диагональ параллелограмма разбивает его на два равных треугольника. Верно ли, что если каждая диагональ четырехугольника разбивает его на два равных треугольника, то этот четырехугольник является параллелограммом?
4. Составьте и докажите задачи о стереометрических объектах аналогичные данным. Результат занесите в таблицу.
| Планиметрическая задача | Стереометрическая задача |
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
(параллелограмм  параллелепипед) параллелепипед)
| Сумма квадратов диагоналей параллелепипеда равна сумме квадратов всех ее ребер. |
Через каждую точку прямой можно провести перпендикулярную ей прямую и притом только одну.
(прямая  плоскость) плоскость)
| |
Сумма расстояний от любой точки, лежащей внутри равностороннего треугольника, до его сторон, есть величина постоянная.
(равносторонний треугольник  правильный тетраэдр) правильный тетраэдр)
| |
Правильный треугольник АВС описан около окружности. Сторона треугольника равна а. Докажите, что  .
(Правильный треугольник .
(Правильный треугольник 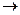 правильная треугольная призма) правильная треугольная призма)
| |
Доказать, что центры вписанной и описанной окружностей правильного треугольника совпадают и делят высоту в отношении 2:1, считая от вершины.
(правильный треугольник  правильный тетраэдр) правильный тетраэдр)
|
5. Разработайте фрагмент урока по использованию аналогии при решении следующих задач:
а) Отношение площадей треугольников, имеющих общие высоты, равно отношению оснований, соответствующим этим высотам. (Отношение объемов пирамид, имеющих …).
б) Отношение площадей треугольников, имеющих общие основания, равно отношению высот, соответствующим этим сторонам треугольника. (Отношение объемов пирамид, имеющих …).
в) Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. (Если трехгранный угол одного тетраэдра …).
г) Отношение площадей подобных треугольников (многоугольников) равно квадрату коэффициента подобия. (Отношение объемов подобных пирамид (многогранников) …).
Сформулируйте тему урока. Подберите задачи, в решении которых используется результат решения полученных по аналогии задач.
6. Расстояние от вершины угла правильного треугольника до центра вписанной окружности радиуса r равно 2 r. Чему равно расстояние от вершины правильного тетраэдра до центра вписанного в него шара? Сделайте предположение по аналогии. Докажите или опровергните его.
7. Все высоты правильного треугольника пересекаются в одной точке, которая делит каждую из высот в отношении 2:1, считая от вершины. В каком отношении делятся высоты правильного тетраэдра, считая от его вершины? Сделайте предположение по аналогии. Докажите или опровергните его.
8. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники подобны. Сделайте предположение по аналогии для четырехугольника. Докажите или опровергните его.
9. Если произведение двух целых чисел делится на 7, то хотя бы один из сомножителей делится на 7. Сделайте предположение по аналогии о делимости произведения двух целых чисел на 8. Докажите или опровергните его.
10. Разработайте фрагмент урока по изучению свойств правильного тетраэдра по аналогии со свойствами правильного треугольника.
11. Составьте тест по любой теме, используя аналогию отношений.
Мышление - это движение мысли, раскрывающее связь, которая ведет от отдельного к общему и от общего к отдельному.
Дж. Пойа
Чтобы провести обобщение, необходимо отвлечься от конкретного содержания и выделить сходное, общее, существенное в структуре предмета задачи, отношений между отдельными ее элементами, отбросить специфические, особенные, единичные признаки и сохранить только общие для группы отдельных элементов.
Способность к обобщению математического материала можно рассматривать с двух сторон:
- способность субъекта увидеть в частном уже известное ему общее (подведение частного случая под известное общее понятие);
- способность увидеть в частном пока еще неизвестное общее (вывести из частных случаев, образовать понятие).
Обобщение означает переход знания на более высокий уровень на основе установления для данных объектов общих свойств или общих отношений.
Обобщение нередко осуществляется путем выделения одинакового математического содержания для различных задач. В качестве примера рассмотрим две задачи.
1. Два населенных пункта расположены по одну сторону от прямой шоссейной дороги. У дороги требуется построить автозаправочную станцию и проложить к ней дороги от населенных пунктов. В каком месте следует построить станцию, чтобы суммарная длина дорог от нее до населенных пунктов была наименьшей?
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 3506; Нарушение авторских прав?; Мы поможем в написании вашей работы!