
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Систем задач
|
|
|
|
Системный подход позволяет выделить четыре этапа конструирования систем задач.
I этап – теоретический. Данный этап включает несколько подэтапов.
1. Выявление совокупности основных знаний и умений, которые должны быть сформированы в процессе изучения темы в соответствии с программными требованиями. Формулировка общих целей изучения данной темы.
2. Установление взаимосвязей между понятиями и фактами внутри темы, а также ее связи с другими темами.
3. Определение необходимых для раскрытия темы видов уроков, а также их конкретизация в соответствии с выделенным программой числом часов на изучение темы.
4. Формулирование частных целей для отдельных уроков и выявление тех знаний и умений, которые должны быть сформированы на каждом из них.
II этап – отборочный. В соответствии с поставленными целями и выделенными на предыдущем этапе особенностями изучаемого материала осуществляется отбор задач в систему. Имеющиеся в учебных пособиях задачи дополняются с помощью приемов обобщения, конкретизации, составления обратных задач, варьирования, составления более сложных задач.
III этап – структурирующий. Между совокупностью отобранных для каждого урока задач устанавливаются взаимосвязи. В соответствии с этими взаимосвязями, а также типами уроков, для которых конструируются системы задач, производится выбор методов конструирования систем, с учетом которых происходит упорядочивание задач.
IV этап – констатирующий. Проверяется соответствие построенных систем задач выделенным системным требованиям. В случае необходимости проводится корректировка сконструированных систем задач.
Заметим, что выделенные этапы конструирования систем задач рассматриваются как идеальная модель данного процесса. На практике данные этапы находятся в очень тесной взаимосвязи и взаимопересечении. Так, например, при отборе задач учитель заранее представляет себе способ их упорядочивания, то есть обращается к структурирующему этапу.
Для успешного прохождения второго и третьего этапов необходимо придерживаться ряда правил.
1. Правило доступности. Каждая задача системы должна быть посильна ученику. Следует оберегать учащихся от непосильных трудностей, заботиться о сохранении интереса к решению задачи.
2. Правило однотипности. В систему необходимо включать однотипные задачи, поскольку это способствует формированию прочных знаний и умений. При подборе или составлении однотипных задач необходимо руководствоваться закономерностью появления неверных ассоциаций, выделенных психологом П.А. Шеваревым. Она состоит в том, что если в процессе обучения выполняются три условия: 1) учащийся выполняет задания одного типа; 2) некоторые несущественные особенности заданий неизменно повторяются; 3) учащийся может получить верный ответ и в том случае, когда не осознает эту особенность, - то степень осознания этой особенности снижается. Например, при решении системы 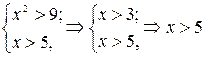 получен правильный ответ. Ошибка не проявилась. При наличии сходных задач, например,
получен правильный ответ. Ошибка не проявилась. При наличии сходных задач, например, 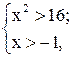 неверная ассоциация закрепляется. Г.И. Саранцевым установлено, что упрочение ошибочной ассоциации, возникающей в соответствии с закономерностью П.А. Шеварева, начинается после трех однотипных упражнений. Таким образом, каждая третья задача должна варьировать несущественные признаки системы задач. В нашем примере такой может быть, например, система
неверная ассоциация закрепляется. Г.И. Саранцевым установлено, что упрочение ошибочной ассоциации, возникающей в соответствии с закономерностью П.А. Шеварева, начинается после трех однотипных упражнений. Таким образом, каждая третья задача должна варьировать несущественные признаки системы задач. В нашем примере такой может быть, например, система 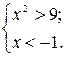
3. Правило разнообразия. Чтобы избежать снижения интереса, внимания и активности учащихся, в систему должны быть включены задачи, разнообразные по форме, содержанию и способу решения.
4. Правило противопоставления. Полезно в систему включать задачи на сходные и взаимообратные понятия, а также задачи, не имеющие решения, и контрпримеры.
5. Правило учета целей. При выборе задач в систему необходимо учитывать цели, которых помогает добиться каждая из них. Нельзя упускать из виду и общие цели их использования, их место в общей системе.
6. Правило ситуативности. При отборе задач нужно предусмотреть, чтобы формируемое действие применялось в различных ситуациях.
7. Правило полноты. Перед отбором задач для системы необходимо выделить все понятия и факты, которые должны усвоить учащиеся, умения и навыки, которые они должны приобретать в процессе решения системы. Все это нужно учитывать, проводя отбор задач.
8. Правило усложнения. Необходимо учитывать сложность каждой задачи в системе и располагать их по мере увеличения сложности.
9. Правило структурности. Система задач может быть разбита на несколько взаимоподчиненных друг другу подсистем.
10. Правило индивидуализации. Следует учитывать, что разным учащимся требуется разное время для решения одной и той же задачи, а также разное количество задач для усвоения одного и того же материала. Система задач должна иметь открытую структуру, то есть у учителя должна быть возможность исключать некоторые задачи системы или менять форму их предъявления.
Первые семь из перечисленных правил служат критериями отбора задач в систему, остальные же отражают основные моменты упорядочивания подобранных задач.
Покажем механизм отбора задач в систему на примере темы 7 класса «Вынесение общего множителя за скобки». Прежде всего учитель должен решить предложенные автором учебника задачи.
Вынесите за скобки общий множитель:
№ 1. 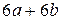 № 2.
№ 2.  № 3.
№ 3.  № 4.
№ 4.  № 5.
№ 5.  № 6.
№ 6.  № 7.
№ 7. 
| № 8.  № 9.
№ 9. 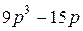 № 10.
№ 10. 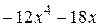 № 11.
№ 11.  № 12.
№ 12. 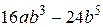 № 13.
№ 13.  № 14.
№ 14. 
|
Разложить на множители:
№ 15. 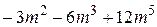 № 16.
№ 16.  № 17.
№ 17. 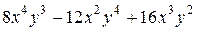 № 18.
№ 18. 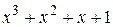
| № 19.  № 20.
№ 20. 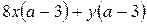 № 21.
№ 21. 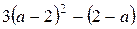 № 22.
№ 22. 
|
Решите уравнения:
№ 23. 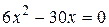
№ 24. 
№ 25. 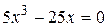
Докажите, что значение выражения:
№ 26. 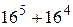 кратно 17
кратно 17
№ 27. 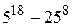 кратно 120
кратно 120
№ 28. 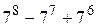 делится на 43
делится на 43
№ 29. 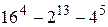 делится на 11
делится на 11
№ 30.Докажите, что сумма трех последовательных натуральных степеней числа 2 делится на 14.
Вынесите за скобки числовой множитель:
№ 31. 
№ 32. 
№ 33. 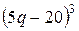
Поставьте вместо многоточия выражение так, чтобы равенство было верным:
№ 34. 
№ 35. 
Для отбора задач можно составить таблицу:
| номера задач правила отбора | |||||||||||||||||||||||||||||||||||
| полноты | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | |||||||||||||||
| доступности | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | |||||||||||||
| противопоставления | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | ||||||||||||
| учета целей | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | ||||||||||||
| однотипности | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | ||||||||||
| разнообразия | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | ||||||||||||||||
| ситуативности | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + |
Обратим внимание на то, что решение вопроса о включении той или иной задачи в систему не всегда должно быть категоричным. Например, правило полноты допускает выбор между несколькими однотипными задачами, решение которых направлено на формирование сходных знаний и умений. Так, в нашей таблице с учетом данного правила вместо задачи № 4 могла быть выбрана задача № 9. То же самое можно сказать и о правилах учета целей, однотипности, разнообразия и ситуативности.
Сначала определим те задачи, которые удовлетворяют большинству правил: № 1, № 2, № 4, № 5, № 7, № 10, № 11, № 13, № 14, № 15, № 17, № 19, № 20, № 22, № 23, № 24, № 26, № 28, № 31, № 32, № 34.
После этого уделим внимание задачам, удовлетворяющим небольшому количеству правил. Если ответ на вопрос: «Почему вы включили в систему именно эту задачу?» удается мотивировать соблюдением соответствующего правила, то эта задача также включается в систему. Так, добавим следующие задачи: № 8 (правило противопоставления), № 21 (правило учета целей), № 27, № 29 (правило однотипности), № 35 (правило разнообразия). Затем рассмотрим задачи, которые однозначно нельзя включать в систему: № 18, № 25 – не удовлетворяют правилу доступности.
Следует заметить, что учитель с опытом способен операции по отбору задач проделывать в уме, не составляя при этом подобную таблицу.
Знание этапов и правил недостаточно для успешного конструирования систем задач. Перед построением системы необходимо выбрать метод, согласно которому будет осуществляться данный процесс. Методы конструирования систем задач рассматриваются в последующих параграфах.
Вопросы и задания
1. Дана совокупность задач на решение линейных неравенств. Расположите эти задачи в порядке нарастания сложности.
№ 1.  № 2.
№ 2.  № 3.
№ 3.  № 4.
№ 4. 
| № 5. 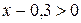 № 6.
№ 6.  № 7.
№ 7.  № 8.
№ 8. 
|
2. Дана совокупность задач на решение линейных неравенств. Расположите эти задачи, соблюдая правило структурности.
№ 1. 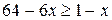 № 2.
№ 2. 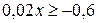 № 3.
№ 3.  № 4.
№ 4. 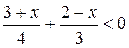 № 5.
№ 5. 
| № 6. 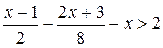 № 7.
№ 7.  № 8.
№ 8. 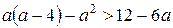 № 9.
№ 9. 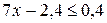 № 10.
№ 10. 
|
3. Расположите вышеперечисленные неравенства так, чтобы при их решении была возможность использования индивидуального подхода. Покажите, как именно он может быть осуществлен.
4. Выполните задания и ответьте на вопросы.
Разложите на множители:
№ 1. 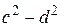
№ 2. 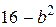
№ 3. 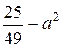
№ 4. 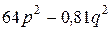
№ 5. 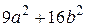
Представьте в виде многочлена:
№ 6. 
№ 7. 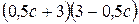
№ 8. 
Вычислите:
№ 9. 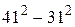
№ 10. 
№ 11. 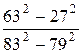
Разложите на множители:
№ 12. 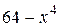
№ 13. 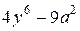
№ 14. 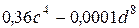
№ 15. 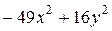
№ 16. 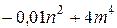
№ 17. 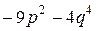
№ 18. 
№ 19. 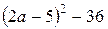
№ 20. 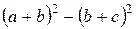
№ 21. 
Заполните пропуски так, чтобы равенство было верным:
№ 22. 
№ 23. 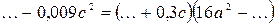
№ 24. 
№ 25.Докажите, что при любом натуральном n значение выражения  делится на 7.
делится на 7.
1) Учтено ли правило полноты и в каких задачах оно находит свое отражение. Повлияет ли на правило полноты: а) добавление в систему задачи на разложение на множители выражения  ; б) удаление из системы задачи № 25? Ответ обоснуйте.
; б) удаление из системы задачи № 25? Ответ обоснуйте.
2) Повлияет ли на правило доступности: а) добавление задачи на разложение на множители выражения 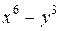 ; б) удаление из системы задачи № 8? Ответ обоснуйте.
; б) удаление из системы задачи № 8? Ответ обоснуйте.
3) Повлияет ли на правило противопоставления: а) добавление задачи на вычисление выражения  ; б) удаление задач № 14, № 17? Ответ обоснуйте.
; б) удаление задач № 14, № 17? Ответ обоснуйте.
4) Повлияет ли на правило учета целей: а) добавление задачи на разложение на множители выражения  ; б) удаление задач № 9 - № 11? Ответ обоснуйте.
; б) удаление задач № 9 - № 11? Ответ обоснуйте.
5) Повлияет ли на правило доступности:
а) добавление задачи на доказательство тождества Диофанта  ;
;
б) удаление задач № 12 - № 21? Ответ обоснуйте.
6) Повлияет ли на правило разнообразия: а) добавление задачи на вычисление 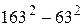 ; удаление задач № 22 - № 24? Ответ обоснуйте.
; удаление задач № 22 - № 24? Ответ обоснуйте.
7) Повлияет ли на правило однотипности: а) добавление еще пяти задач на непосредственное применение формулы разности квадратов; б) удаление задачи № 13. Ответ обоснуйте.
8) Повлияет ли на правило ситуативности: а) добавление задачи 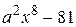 ; удаление задач № 15, № 16? Ответ обоснуйте.
; удаление задач № 15, № 16? Ответ обоснуйте.
5. Используя школьный учебник, произвести выбор задач по какой-либо теме, опираясь сначала только на два правила отбора, затем на три правила и так далее до одновременного соблюдения всех семи правил.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2054; Нарушение авторских прав?; Мы поможем в написании вашей работы!