Варьирование задачи

Конструирование систем задач

Суть метода варьирования задачи состоит в том, что каждая задача системы получена из данной задачи путем варьирования ее содержания или формы. Напомним, что под содержанием задачи понимается совокупность ее компонентов: условие, требование, базис и способ решения.

Основные приемы варьирования – прием взаимообратных и противоположных задач, прием обобщения и конкретизации, прием аналогии. Решение одной и той же задачи разными методами – пример варьирования способа решения задачи.

		Базис
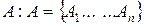
	Условие:	Способ решения	Требование:
		Варьирование компонентов задачи

Прием отрицания и составления взаимообратных задач

Прием обобщения и конкретизации

Прием аналогии

Приведем пример варьирования условия. Исходная задача: «Правильная треугольная пирамида FABC, где АВ=2, FA=3. Найти площадь сечения пирамиды плоскостью, проходящей через середины ребер АВ и АС и точку D на ребре FA, где AD:DF=2:1».

Варьируем условие, заменяя «точку D на ребре FA, где AD: DF=2:1» условием

· «параллельно апофеме грани (BFC);

· «параллельно высоте FO»;

· «перпендикулярно ребру AF»;

· «перпендикулярно грани (BFC)».

Получаем систему задач.

Рассмотрим вопросы методики варьирования задачи.

На начальном этапе формирования умений и навыков следует варьировать только внешнюю форму задачи, оставляя постоянным ее содержание. Это дает возможность учащимся сделать самостоятельное обобщение ряда решений других задач и осуществить подготовку качественного скачка достаточными количественными изменениями. На последующих этапах для обеспечения полноты системы задач недостаточно одного лишь варьирования их внешней формы. Необходимо стремиться к разнообразию задач системы, которое призвано поддерживать должную напряженность процесса решения.

Варьирование условия задачи не должно быть произвольным. Когда условие меняется калейдоскопически, учащимся трудно сосредоточить внимание на существенных связях между данными, понять роль варьирующего элемента. В методической литературе выделяют два взаимообратных приема варьирования некоторого элемента условия задачи.

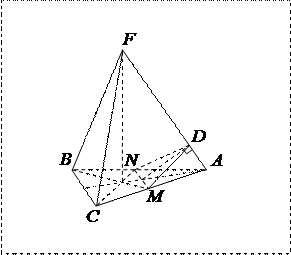
Применение первого предполагает при переходе от одной задачи к другой инвариантность всех их звеньев кроме одного. Например, при изучении линейной функции учащимся предлагается построить графики функций 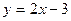, , , . После выполнения задания учащиеся должны сделать вывод о параллельности прямых имеющих одинаковый угловой коэффициент.

Второй прием – обратный первому – варьируется то звено внешней формы, уяснение роли которого является целью в данный момент. Например, , , 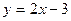, , . Решение данной системы задач позволяет учащимся установить факт зависимости знака углового коэффициента от характера монотонности прямой.

Приведем пример варьирования способа решения.

Решите уравнение .

I способ – разложение на множители.

А: ; ; ; ; , .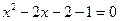

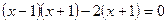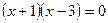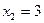Б: ; ; ; , .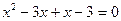

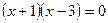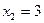II способ – выделение квадрата двучлена. ; ; 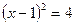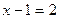или ; , .

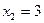III способ – нахождение корней квадратного уравнения по формуле.

, , , .

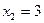IV способ – нахождение корней квадратного уравнения по теореме Виета.

Решая систему подбором, находим корни уравнения.

Рассмотрим пример варьирования требования задачи.

Основанием треугольной призмы является правильный треугольник со стороной а. Одна из вершин верхнего основания проецируется в центр нижнего. Боковое ребро призмы равно b. Найдите: а) высоту призмы; б) объем призмы; в) площадь боковой поверхности; г) площадь сечения призмы плоскостью, перпендикулярной плоскостям оснований и проходящей через вершину верхнего основания; д) площадь сечения призмы плоскостью, перпендикулярной плоскостям оснований и проходящей через сторону нижнего основания.

Решение каждой задачи системы, взятой в отдельности, достаточно трудоемко и требует больших временных затрат. При последовательном решении задач можно воспользоваться результатами, полученными в предыдущих задачах; акцентировать внимание не на вычислении элементов, а на определении их расположения относительно друг друга, на доказательстве факта о взаимном расположении.

Далее дадим краткую характеристику приемам построения взаимообратных и противоположных задач, аналогии, обобщения и конкретизации.

Вопросы и задания

1. Поочередно варьируя условие, составьте несколько задач из следующей: «Найдите высоту равнобедренного треугольника с боковой стороной 12 см и углом 120°».

2. Дана задача: «Найдите радиус окружности, описанной около прямоугольного треугольника с катетами 6 см и 8 см». Составьте различные заключения задачи.

3. В треугольнике АВС из вершины В к стороне АС проведен отрезок BD. Найдите величину угла DBC, если а) AD = BD = CD, Ð CAB = 30°;

б) AD = BD, Ð ABC = 75°; Ð ADB = 150°; в) BD = CD, Ð ADB = 40°.

Расположите требования в порядке возрастания сложности. Опишите фрагмент урока по решению данной задачи.

4. Решите задачу: «В основании призмы лежит правильный треугольник со стороной а. Боковое ребро призмы равно b, а углы между одним из боковых ребер и прилежащими к нему сторонами основания – 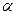. Найдите площадь боковой поверхности и объем призмы, площадь сечения призмы плоскостью, проходящей через сторону нижнего основания перпендикулярно верхнему основанию». На данном примере покажите эффективность варьирования требования задачи.

Дата добавления: 2014-12-16