
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Двух положительных чисел
|
|
|
|
Среднее арифметическое и среднее геометрическое
Ключевая задача. Если  ,
, 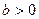 , то
, то  .
.
Следствие. 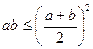 .
.
1. Докажите, что при  ,
, 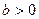 ,
,  ,
, 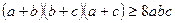 .
.
На основании теоремы о среднем арифметическом и среднем геометрическом для положительных чисел а и b, b и с, а и с запишем неравенства:  ;
;  ;
;  .
.
Так как левая и правая части этих неравенств положительны, то эти неравенства можно почленно перемножить, в результате чего получим:  ;
; 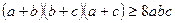 .
.
2. Докажите, что при  ,
, 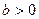 ,
, 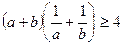 .
.
Применим теорему о среднем арифметическом и среднем геометрическом для положительных чисел а и b,  и
и 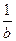 :
:  ,
,  .
.
Перемножив почленно эти неравенства, получим 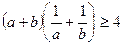 .
.
3. Докажите, что при  ,
, 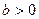 ,
,  ,
,  .
.
Запишем на основании теоремы о среднем арифметическом и среднем геометрическом неравенства для пар чисел  и
и 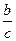 ,
, 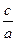 и 1:
и 1:
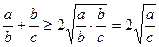 ,
, 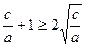 .
.
Сложим неравенства почленно, получим: 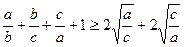 .
.
Запишем теорему о среднем арифметическом и среднем геометрическом для чисел  и
и  :
:  .
.
Тогда 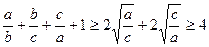 ;
;  .
.
4. Докажите, что при  ,
, 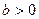 ,
,  ,
,  ,
,  .
.
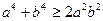 ;
; 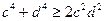 ;
;
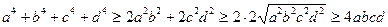 .
.
5. Докажите, что при  ,
, 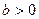 ,
,  ,
,  .
.
Разложим квадрат суммы трех чисел: 
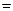

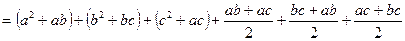 .
.
Применим теорему о среднем арифметическом и среднем геометрическом ко всем слагаемым:
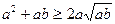 ;
;  ;
;  ;
; 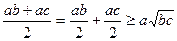 ;
;
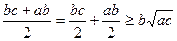 ;
; 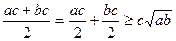 .
.
Сложим неравенства почленно, получим: 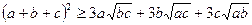 или
или  .
.
6. Докажите, что 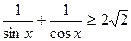 при
при 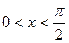 .
.
При 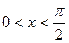 значения
значения 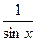 и
и 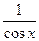 положительны, а значит, по теореме о среднем арифметическом и среднем геометрическом для двух положительных чисел имеем:
положительны, а значит, по теореме о среднем арифметическом и среднем геометрическом для двух положительных чисел имеем: 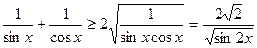 .
.
Для 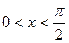 очевидно, что
очевидно, что 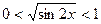 , или
, или 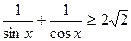 .
.
7. Докажите, что при  ,
, 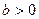 ,
,  ,
, 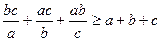 .
.
8. Докажите, что при  ,
, 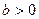 ,
,  ,
, 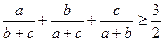 .
.
9. Докажите, что при  ,
, 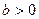 ,
,  ,
, 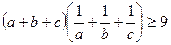 .
.
10. Докажите, что при  ,
, 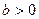 ,
,  ,
, 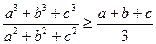 .
.
11. Докажите, что при  ,
, 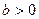 ,
,  ,
, 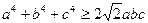 .
.
12. Докажите, что при  ,
, 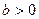 ,
,  ,
,  .
.
13. Докажите, что из всех прямоугольником с заданным периметром наибольшую площадь имеет квадрат.
Пусть периметр прямоугольника равен p, а одна из сторон –  , тогда длина другой стороны равна
, тогда длина другой стороны равна 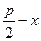 .
. 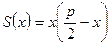 .
.
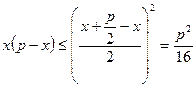 ;
; 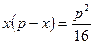 ;
; 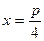 .
.
Так как 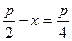 при
при 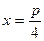 , наибольшую площадь имеет прямоугольник с равными сторонами, то есть квадрат.
, наибольшую площадь имеет прямоугольник с равными сторонами, то есть квадрат.
14. Докажите, что из всех прямоугольником с заданной площадью наименьший периметр имеет квадрат.
Пусть одна из сторон прямоугольника имеет длину  , а его площадь –
, а его площадь –  , тогда длина другой стороны –
, тогда длина другой стороны –  .
. 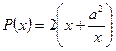 .
.
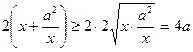 ;
; 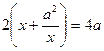 ;
;  ;
; 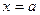 .
.
Так как  при
при 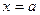 , то наименьший периметр имеет прямоугольник с равными сторонами, то есть квадрат.
, то наименьший периметр имеет прямоугольник с равными сторонами, то есть квадрат.
15. Даны измерения а, b, с прямоугольного параллелепипеда. Можно ли подобрать такие числовые значения а, b, с, чтобы объем прямоугольного параллелепипеда был больше  суммы объемов кубов с ребрами а, b, с?
суммы объемов кубов с ребрами а, b, с?
Объем прямоугольного параллелепипеда можно записать в виде  . По теореме о среднем арифметическом и среднем геометрическом для трех положительных чисел
. По теореме о среднем арифметическом и среднем геометрическом для трех положительных чисел  ,
, 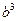 ,
, 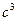 имеем
имеем  . Таким образом, нельзя подобрать такие числовые значения а, b, с, удовлетворяющие условию задачи.
. Таким образом, нельзя подобрать такие числовые значения а, b, с, удовлетворяющие условию задачи.
16. Найдите максимальный объем прямоугольного параллелепипеда, если задана площадь его полной поверхности.
Пусть а, b, с – измерения прямоугольного параллелепипеда, 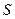 – площадь полной поверхности,
– площадь полной поверхности,  – объем. Тогда
– объем. Тогда  ,
, 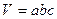 .
.
Или 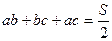 , а
, а  .
.
Тогда 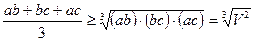 ;
; 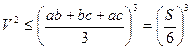 ;
;  .
.
Равенство достигается, если  . То есть из всех прямоугольных параллелепипедов с данной площадью поверхности наибольший объем имеет куб.
. То есть из всех прямоугольных параллелепипедов с данной площадью поверхности наибольший объем имеет куб.
17. Решите уравнение  .
.
Первое слагаемое из левой части запишем в виде 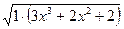 и это есть среднее геометрическое 1 и
и это есть среднее геометрическое 1 и  , тогда
, тогда 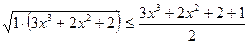 ;
;  .
.
Аналогично, 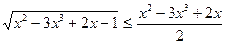 .
.
 .
.
Раз левая часть исходного уравнения не больше выражения 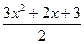 , то и его правая часть должна обладать тем же свойством, то есть
, то и его правая часть должна обладать тем же свойством, то есть
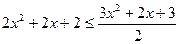 .
.
Решим это неравенство: 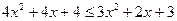 ;
;  ;
;  ;
; 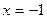 .
.
18. Решите уравнение  .
.
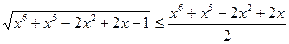 ;
; 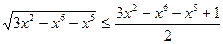 ;
;
 ;
;
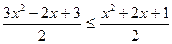 ;
;  ;
;  ;
; 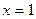 .
.
19. При каком значении аргумента функция принимает наибольшее значение?
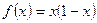 ,
,  .
.
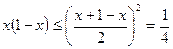 ;
;  ;
; 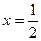 .
.
20. При каком значении аргумента функция принимает наибольшее значение? 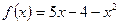 ,
,  .
.
 ;
;  ;
; 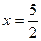 .
.
21. При каком значении аргумента функция принимает наименьшее значение?  ,
, 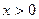 .
.
 ;
; 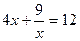 ;
;  .
.
22. При каком значении аргумента функция принимает наименьшее значение? 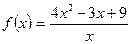 ,
, 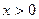 .
.
 ;
; 
23. При каком значении аргумента функция принимает наименьшее значение? 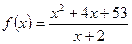 ,
, 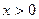 .
.
 ;
; 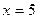 .
.
24. При каком значении аргумента функция принимает наименьшее значение? 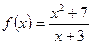 ,
,  .
.
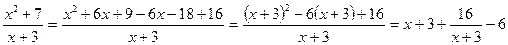 .
.
 ;
; 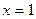 .
.
См.: Генкин Г.З. Задачи на нахождение экстремумов функций в VII классе // Математика в школе. – № 9. – 2003. – с.51-54.
Далингер В.А. Как сделать теорему о среднем арифметическом и среднем геометрическом средством познания // Математика в школе. – № 9. – 2003. – с.54-56.
Приложение 2
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 904; Нарушение авторских прав?; Мы поможем в написании вашей работы!