Длина биссектрисы

Ключевая задача. Докажите, что если две стороны треугольника равны a и b, угол между ними равен 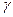, то длина биссектрисы, проведенной к третьей стороне, может быть вычислена по формуле: .

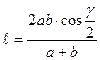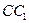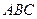Доказательство. Пусть – биссектриса треугольника . Тогда

или 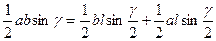. После несложных преобразований получим .

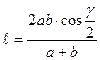Задачи системы:

1.В треугольнике 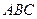выполняется соотношение . Найдите градусную меру угла А.

2. Найдите площадь треугольника, если две его стороны равны 35 см и 14 см, а биссектриса угла между ними содержит 12 см.

3. Плоскость отсекает от боковых ребер SA, SB, SC правильной четырехугольной пирамиды SABCD отрезки SК, SL, SM, причем , , . Длина бокового ребра равна а. Найдите длину отрезка SN, отсекаемого этой плоскостью на ребре SD.

Приложение 5

Длина медианы

Ключевая задача. Докажите, что если стороны АВ, АС и ВС треугольника АВС равны соответственно с, b и а, то длина медианы, проведенной к стороне ВС, может быть вычислена по формуле _.

Доказательство.

I способ. Достроим треугольник до параллелограмма. Тогда по свойству диагоналей параллелограмма имеем 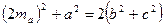. Отсюда .

II способ. , 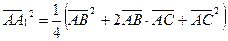или 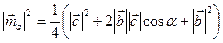. По теореме косинусов имеем: . Отсюда .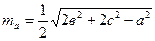

Задачи системы:

1. Найдите площадь треугольника, если его две стороны равны 1см и см, а медиана третьей стороны равна 2 см.

Решение.

1. Найдем АС, используя формулу длины медианы. . .

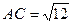2. _ΔАВС – прямоугольный, так как . Следовательно, .

Ответ: 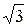см².

2. В равнобедренном прямоугольном треугольнике медианы, проведенные к катетам, содержат по l см. Найдите площадь треугольника.

Решение.

Пусть катет прямоугольного равнобедренного треугольника равен а. Тогда . Из формулы длины медианы, выразим 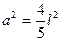. Тогда .

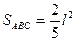3. В равнобедренном треугольнике к боковой стороне, длиной 4 см, проведена медиана, длиной 3 см. Найдите основание треугольника.

4. Длины двух сторон треугольника 27см и 29см. Длина медианы, проведенной к третьей стороне, равна 26см. Найдите высоту треугольника, проведенную к стороне длиной 27см.

5. Основание треугольника 14 см, а медианы, проведенные к двум другим сторонам, равны 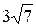и 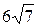. Найдите длины неизвестных сторон треугольника.

Решение.

Пусть 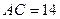, , . Тогда длины медиан АА₁ и СС₁ можно найти по формулам: 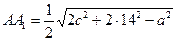и .

Имеем систему:

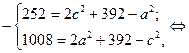
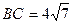Ответ: см, см.

6. Медианы треугольника равны 5см, 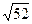см и 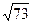см. Докажите, что треугольник прямоугольный.

7. Найдите отношение суммы квадратов всех медиан треугольника к сумме квадратов всех его сторон.

Приложение 6

Дата добавления: 2014-12-16