
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Являются серединами сторон данного четырехугольника
|
|
|
|
Четырехугольник, вершины которого
Ключевая задача. Середины сторон произвольного четырехугольника являются вершинами параллелограмма.
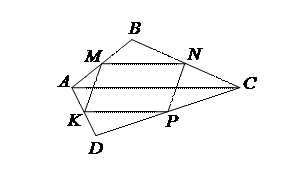
| ABCD – выпуклый четырехугольник. M, N, P, K – середины сторон АВ, ВС, CD и АD соответственно. Отрезок MN параллелен диагонали АС и равен ее половине по свойству средней линии. Аналогично, отрезок PK параллелен АС и равен ее половине. Следовательно, отрезки MN и PK равны и параллельно. По признаку MNPK – параллелограмм. |
Для невыпуклого и пространственного четырехугольников доказательство аналогичное.
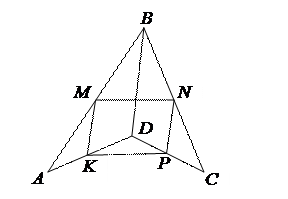
|

|
Следствия:
1. Если ABCD – выпуклый четырехугольник и M, N, P, K – середины его сторон АВ, ВС, CD и AD соответственно, то  .
.
Доказательство.
Треугольники MBN и АВС подобны, следовательно,  . Аналогично,
. Аналогично,  .
.  .
.
Аналогично,  ,
, 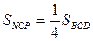 ,
,  .
.
Имеем,  .
.
2. Середины сторон прямоугольника являются вершинами ромба.
3. Середины сторон равнобедренной трапеции являются вершинами ромба.
4. Середины сторон ромба являются вершинами прямоугольника.
Осмыслению ключевой задачи будут способствовать вопросы:
Каким условиям должны удовлетворять диагонали данного четырехугольника, чтобы середины его сторон были вершинами прямоугольника, ромба, квадрата?
Докажите, что середины сторон трапеции со взаимно перпендикулярными диагоналями являются вершинами прямоугольника.
Составьте обратную задачу. Верна ли она?
Задачи системы:
1. Докажите, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Решение.

| Пусть медианы АА1 и СС1 пересекаются в точке О. Отметим точки К и Р – середины отрезков АО и СО. Тогда точки К, Р, С1 и А1 середины сторон невыпуклого четырехугольника АВСО. Следовательно, по ключевой задаче КРС1А1 – параллелограмм. Его диагонали точкой пересечения делятся пополам. Тогда АО:ОА1=СО:ОС1=2:1. |
Рассуждая аналогично, докажем, что медианы АА1 и ВВ1 пересекаются в точке Q и АQ:QА1=ВQ: QВ1=2:1. Так как отрезок АА1 делится в отношении 2:1, считая от точки А, однозначно, то точки О и Q совпадают. Следовательно, медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
2. Докажите, что отрезки, соединяющие середины сторон скрещивающихся ребер тетраэдра пересекаются в одной точке.
Решение.

| По ключевой задаче MKPN и MLPR – параллелограммы. Их диагонали пересекаются в одной точке и делятся ею пополам. |
3. Диагонали трапеции взаимно перпендикулярны, длина одной из них равна 6 см. Длина отрезка, соединяющего середины оснований, равна 5 см. Найдите площадь трапеции.
Решение.

| Пусть M и P – середины боковых сторон трапеции. Тогда по ключевой задаче MNPK – прямоугольник. Так как  см, то см, то  см. По теореме Пифагора из прямоугольного треугольника MNK см. По теореме Пифагора из прямоугольного треугольника MNK  см. Тогда см. Тогда  см2, а см2, а 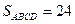 см2. см2.
|
4.В выпуклом четырехугольнике длины диагоналей 2 см и 4 см. Найдите площадь четырехугольника, зная, что длины отрезков, соединяющих середины противоположных сторон равны.
Решение.

| По ключевой задаче MNPK – параллелограмм. Так как его диагонали равны, то MNPK – прямоугольник. Диагонали данного выпуклого четырехугольника параллельны сторонам прямоугольника и, следовательно, перпендикулярны. Найдем площадь выпуклого четырехугольника как половину произведения диагоналей на синус угла между ними.  см2. см2.
|
5.В выпуклом четырехугольнике ABCD длина отрезка, соединяющего середины сторон AB и CD, равна одному метру. Прямые BC и АD перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей AC и ВD.
Решение.
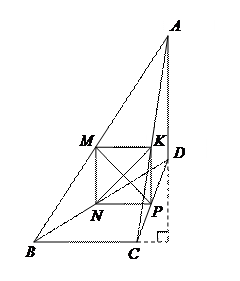
| Обозначим через M, N, P, K – середины сторон АВ, ВD, CD и АС соответственно. Тогда MK║NP║BC как средние линии треугольников BAC и BDC. Аналогично, MN║KP║AD. Поэтому параллелограмм MNPK является прямоугольником и 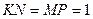 м. м.
|
6. В выпуклом пятиугольнике ABCDE с единичными сторонами середины P, Q сторон AB,CD и S,T сторон BC,DE соединены отрезкамиPQ и ST. Пусть M и N – середины отрезков PQ и ST. Найдите длину MN.
Решение.

|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 6488; Нарушение авторских прав?; Мы поможем в написании вашей работы!