Питання для самоперевірки. Якщо відомий який-небудь частинний ненульовий розв’язок рівняння (7), то це рівняння розв’язується в квадратурах

Приклад 6.4.

Теорема 5.

Якщо відомий який-небудь частинний ненульовий розв’язок рівняння (7), то це рівняння розв’язується в квадратурах.

Розв’язати рівняння 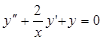, яке має частинний розв’язок .

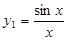● Згідно з теоремою 5 покладемо 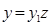, тоді матимемо рівняння

.

Підставимо замість 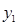, його значення і розв'яжемо відносно функції :

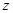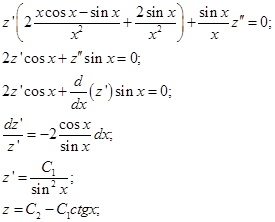
Отже, . ●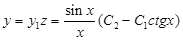

1. Що називається лінійним диференціальним рівнянням n-го порядку?

2. Що називається лінійним однорідним диференціальним рівнянням другого порядку?

3. Що називається визначником Вронського для функцій y₁(x) та y₂(x)?

4. Сформулювати теорему про структуру загального розв’язку лінійного однорідного диференціального рівняння другого порядку.

5. Як знайти загальний розв’язок лінійного однорідного рівняння другого порядку, якщо відомий його частинний розв’язок?

6. Що називається однорідним диференціальним рівнянням другого порядку із сталими коефіцієнтами?

7. Яке рівняння називається характеристичним? Як його знаходять?

8. Який вигляд має загальний розв’язок лінійного однорідного рівняння другого порядку із сталими коефіцієнтам, якщо корені характеристичного рівняння:

а) дійсні і різні;

б) дійсні і рівні;

в) комплексні.

Дата добавления: 2014-12-17