
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальні системи рівнянь
|
|
|
|
ТЕМА 8. Системи диференціальних рівнянь
ВПРАВИ
І Знайти загальні розв’язки лінійних неоднорідних рівнянь із сталими коефіцієнтами (рівняння із спеціальною правою частиною).
1.  ; 5.
; 5.  ; 9.
; 9. 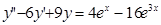 ;
;
2. 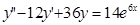 ; 6.
; 6. 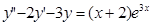 ; 10.
; 10. 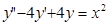
3. 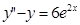 ; 7.
; 7. 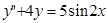 ;
;
4.  ; 8.
; 8.  ;
;
ІІ Знайти частинні розв’язки лінійних неоднорідних рівнянь із сталими коефіцієнтами (рівняння із спеціальною правою частиною).
1.  ;
;
2.  .
.
ІІІ Розв’язати рівняння, використовуючи метод варіації довільної сталої.
1. 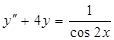 ; 6.
; 6.  ;
;
2. 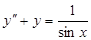 ; 7.
; 7.  ;
;
3.  ; 8.
; 8.  ;
;
4.  ; 9.
; 9. 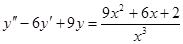 ;
;
5. 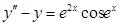 ; 10.
; 10.  .
.
ІV Знайти розв’язок задачі Коші
1. 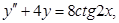
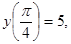
 ;
;
2. 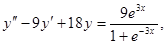
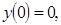
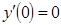 ;
;
3. 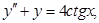
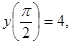
 ;
;
4. 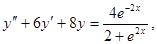
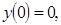
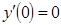 ;
;
5. 

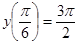 ;
;
6. 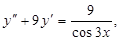
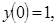
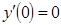 ;
;
7. 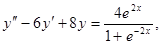
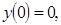
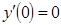 ;
;
8. 

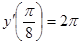 ;
;
9. 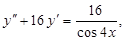
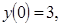
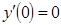 ;
;
10. 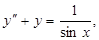
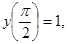
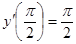 ;
;
11. 
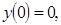
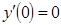 ;
;
12. 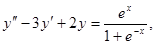
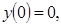
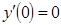 ;
;
13. 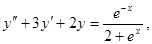
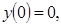
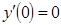 ;
;
14. 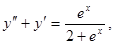
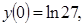
ТЕОРЕТИЧНИЙ МАТЕРІАЛ
Розглянемо деякі найпростіші системи диференціальних рівнянь. Незалежну змінну позначемо буквою 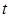 , а невідомі функції – через
, а невідомі функції – через  або (якщо їх не більше трьох) через
або (якщо їх не більше трьох) через  .
.
Нормальною системою диференціальних р івнянь називається система виду:
 (1)
(1)
або 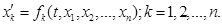
Іншими словами, якщо в лівій частині рівняння системи (1) стоять похідні першого порядку, а праві частини рівнянь зовсім не містять похідних, то така система називається нормальною. Розв’язком системи (1) називається сукупність функцій  , які задовольняють кожному з рівнянь цієї системи.
, які задовольняють кожному з рівнянь цієї системи.
Введенням нових змінних, будь-яке диференціальне рівняння 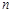 –го порядку, розв’язане відносно старшої похідної, зводиться до еквівалентної системи
–го порядку, розв’язане відносно старшої похідної, зводиться до еквівалентної системи 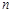 рівнянь першого порядку.
рівнянь першого порядку.
Справді, нехай задано рівняння n-го порядку: 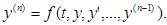

 Покладемо:
Покладемо: 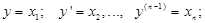

тоді
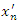
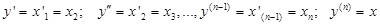 ..
..
Дістали нормальну систему:
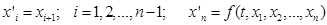 ,
,
еквівалентну заданому рівнянню.
Покажемо, що можливий і зворотній перехід: нормальну систему рівнянь можна замінити одним рівнянням, порядок якого дорівнює числу рівнянь системи. Нехай задана нормальна система (1). Продиференціюємо по 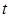 будь-яке, наприклад, перше рівняння:
будь-яке, наприклад, перше рівняння:
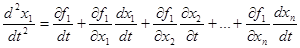 .
.
Підставивши в цю рівність значення похідних 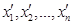 з системи (1), дістанемо
з системи (1), дістанемо  .
.
Аналогічно знаходимо похідні до n-го порядку включно:
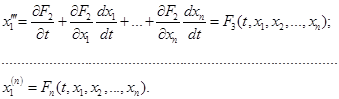
Дістаємо систему рівнянь:
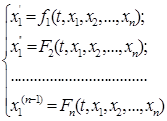 (2)
(2)
Якщо з перших  рівнянь системи (2) знайти (коли це можливо) змінні
рівнянь системи (2) знайти (коли це можливо) змінні
 (3)
(3)
і підставивши їхні значення в останнє рівняння, то одержимо рівняння 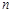 -го порядку відносно змінної
-го порядку відносно змінної  :
:
 . (4)
. (4)
Нехай 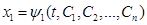 (5)
(5)
(де 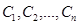 - довільні сталі) – розв'язок рівняння (4). Продиференціювавши його
- довільні сталі) – розв'язок рівняння (4). Продиференціювавши його  разів і підставивши значення похідних
разів і підставивши значення похідних  в рівняння (3), дістанемо
в рівняння (3), дістанемо
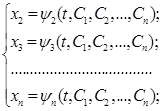 (6)
(6)
Можна довести, що сукупність функцій (5), (6) буде загальним розвязком системи (2).
Для нормальної системи (2) справджується теорема Коші про існування і єдиність: якщо в деякій області G функції 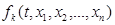 , k=1,2,…,n системи (2) неперервні разом з усіма своїми похідними, i,k= 1,2,…, n,то для будь-якої точки
, k=1,2,…,n системи (2) неперервні разом з усіма своїми похідними, i,k= 1,2,…, n,то для будь-якої точки  існує єдиний розв'язок
існує єдиний розв'язок  , який задовольняє початкові умови:
, який задовольняє початкові умови: 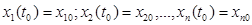 .
.
Для інтегрування системи (2) можна застосовувати метод, за допомогою якого ця система була зведена до рівняння (4). Цей метод називають методом виключення змінної.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 1948; Нарушение авторских прав?; Мы поможем в написании вашей работы!